Тема 4. Дискретные случайные величины

 

4.1. Закон распределения вероятностей дискретной случайной величины.
Законы биномиальный и Пуассона

 

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (т. е. между двумя соседними возможными значениями нет возможных значений), которые эта величина принимает с определенными вероятностями. Другими словами, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (в последнем случае множество всех возможных значений называют счетным).

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины X может быть задан в виде таблицы, первая строка которой содержит возможные значения x_i, а вторая – вероятности р_i:

X x₁ x₂ … x_n

p p₁ p₂ … p_n

где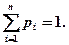

Если множество возможных значений X бесконечно (счетно), то ряд p₁ + p₂ + … сходится и его сумма равна единице.

Закон распределения дискретной случайной величины X может быть также задан аналитически (в виде формулы)

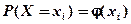
или с помощью функции распределения (см. тему 6, п. 6.1).

Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки M₁(x₁; p₁), M₂(x₂; p₂), …, M_n(x_n; p_n) (x_i – возможные значения X, р_i – соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Биномиальным называют закон распределения дискретной случайной величины X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна р; вероятность возможного значения X = k (числа k появлений события) вычисляют по формуле Бернулли:

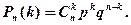
Если число испытаний велико, а вероятность р появления события в каждом испытании очень мала, то используют приближенную формулу

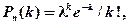
где k – число появлений события в n независимых испытаниях, λ = np (среднее число появлений события в n испытаниях), и говорят, что случайная величина распределена по закону Пуассона.

 

89. Дискретная случайная величина X задана законом распределения:

X 1 3 6 8

p 0,2 0,1 0,4 0,3

Построить многоугольник распределения.

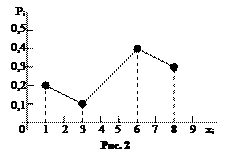
Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения х_i, а по оси ординат – соответствующие вероятности р_i. Построим точки:

M₁(1; 0,2), M₂(3; 0,1), M₃(6; 0,4), и M₄(8; 0,3). Соединив эти точки отрезками прямых, получим искомый многоугольник распределения (рис. 2).

 

90. Дискретная случайная величина Х задана законом распределения:

а) X 2 4 5 6 б) Х 10 15 20

p 0,3 0,1 0,2 0,4 р 0,1 0,7 0,2

Построить многоугольник распределения.

91. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

92. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.

93. После ответа студента на вопросы экзаменационного билета экзаменатор задает студенту дополнительные вопросы. Преподаватель прекращает задавать дополнительные вопросы, как только студент обнаруживает незнание заданного вопроса. Вероятность того, что студент ответит на любой заданный дополнительный вопрос, равна 0,9. Требуется: а) составить закон распределения случайной дискретной величины X – числа дополнительных вопросов, которые задаст преподаватель студенту; б) найти наивероятнейшее число k₀ заданных студенту дополнительных вопросов.

94. Из двух орудий поочередно ведется стрельба по цели до первого попадания одним из орудий. Вероятность попадания в цель первым орудием равна 0,3, вторым – 0,7. Начинает стрельбу первое орудие. Составить законы распределения дискретных случайных величин X и Y – числа израсходованных снарядов соответственно первым и вторым орудием.

95. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.

96. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно три; б) менее трёх; в) более трёх; г) хотя бы одно.

97. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятности того, что магазин получит разбитых бутылок: а) ровно две; б) менее двух; в) более двух; г) хотя бы одну.

Указание. Принять е^-3 = 0,04979.

98. а) Устройство состоит из большого числа независимо работающих элементов с одинаковой (очень малой) вероятностью отказа каждого элемента за время Т. Найти среднее число отказавших за время Т элементов, если вероятность того, что за это время откажет хотя бы один элемент, равна 0,98.

 

Решение. Из условия задачи следует (поскольку число элементов велико, элементы работают независимо и вероятность отказа каждого элемента мала), что число отказов распределено по закону Пуассона, причем требуется найти параметр λ (среднее число отказов).

Вероятность того, что откажет хотя бы один элемент, по условию равна 0,98, следовательно, 1 – e^—λ = 0,98. Отсюда

По таблице функции e^—x находим λ = 3,9. Итак, за время Т работы устройства откажет примерно четыре элемента.

б) Найти среднее число λ, бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0,95. Предполагается, что число бракованных изделий в рассматриваемой партии распределено по закону Пуассона.

Указание. Принять е^-3 = 0,05.

 

99. Доказать, что сумма вероятностей числа появлений события в независимых испытаниях, вычисленных по закону Пуассона, равна единице. Предполагается, что испытания производятся бесчисленное количество раз.

100. Вероятность выигрыша по одному лотерейному билету р = 0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью Р, не меньшей, чем 0,95?

 

Простейший поток событий

 

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.

Простейшим (пуассоновским) называют поток событий, которые обладают следующими тремя свойствами: стационарностью, «отсутствием последействия» и ординарностью.

Свойство стационарности состоит в том, что вероятность появления k событий в любом промежутке времени зависит только от числа k и от длительности t промежутка времени и не зависит от начала его отсчёта. Другими словами, вероятность появления k событий за промежуток времени длительностью t есть функция, зависящая только от k и t.

Свойство «отсутствия последействия» состоит в том, что вероятность появления k событий в любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, предыстория потока не влияет на вероятности появления событий в ближайшем будущем.

Свойство ординарности состоит в том, что появление двух или более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного события за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления только одного события.

Интенсивностью потока λ называют среднее число событий, которые появляются в единицу времени.

Если постоянная интенсивность потока λ известна, то вероятность появления k событий простейшего потока за время t определяется формулой Пуассона

 

Замечание. Поток, обладающий свойством стационарности, называют стационарным; в противном случае – нестационарным.

 

101. Показать, что формулу Пуассона, определяющую вероятность появления k событий за время длительностью t

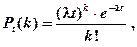
можно рассматривать как математическую модель простейшего потока событий; другими словами, показать, что формула Пуассона отражает все свойства простейшего потока.

102. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трем. Найти вероятность того, что за 2 мин поступит: а) четыре вызова; б) менее четырех вызовов; в) не менее четырех вызовов.

103. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 4 мин поступит: а) три вызова; б) менее трех вызовов; в) не менее трех вызовов. Поток вызовов предполагается простейшим.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: