 |
Локальная и интегральная теоремы Лапласа
|
|
|
|
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)
Здесь
Таблица функции φ(x) для положительных значений х приведена в приложении 1; для отрицательных значений х пользуются этой же таблицей [функция φ(x) четная, следовательно, φ(-x) = φ(x) ].
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < I), событие наступит не менее k1 раз и не более k2 раз, приближенно равна
Здесь
– функция Лапласа,
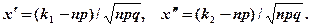
Таблица функции Лапласа для положительных значений x (0 ≤ x ≤ 5) приведена в приложении 2; для значений х > 5 полагают Ф(x) = 0,5. Для отрицательных значений х используют эту же таблицу, учитывая, что функция Лапласа нечетная [ Ф(‑x) = ‑Ф(x) ].
64. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение. По условию, n = 243; k = 70; р = 0,25; q = 0,75. Так как n = 243 – достаточно большое число, воспользуемся локальной теоремой Лапласа:
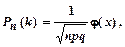
где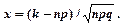 
Найдём значение x:
По таблице приложения 1 найдём φ(1,37) = 0,1561. Искомая вероятность
65. Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.
66. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
67. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.
|
|
|
68. Монета брошена 2N раз (N велико!). Найти вероятность того, что «герб» выпадет ровно N раз.
69. Монета брошена 2N раз. Найти вероятность того, что «герб» выпадет на 2m раз больше, чем надпись.
70. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна р = 0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.
71. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?
3.3. Отклонение относительной частоты от постоянной вероятности
в независимых испытаниях
Оценка отклонения относительной частоты от постоянной вероятности. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа ε, приближенно равна удвоенной функции Лапласа при 
:
72. Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,04.
Решение. По условию, n = 625; p = 0,8; q = 0,2; ε = 0,04. Требуется найти вероятность 
. Воспользуемся формулой
Имеем
По таблице приложения 2 найдём Ф(2,5) = 0,4938. Следовательно, 2Ф(2,5) =2 * 0,4938 = 0,9876. Итак, искомая вероятность приближённо равна 0,9876.
73. Вероятность появления события в каждом из 900 независимых испытаний равна 0,5. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.
|
|
|
74. Вероятность появления события в каждом из 10 000 независимых испытаний равна 0,75. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,01.
75. Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний n, при котором с вероятностью 0,7698 можно ожидать, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.
76. Сколько раз нужно бросить игральную кость, чтобы вероятность неравенства
была не меньше чем вероятность противоположного неравёнства, где m – число появлений одного очка в n бросаниях игральной кости?
77. Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число ε, чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности 0,8 не превысила ε.
78. Отдел технического контроля проверяет на стандартность 900 деталей. Вероятность того, что деталь стандартна, равна 0,9. Найти с вероятностью 0,95 границы, в которых будет заключено число m стандартных деталей среди проверенных.
3.4. Наивероятнейшее число появлений события
в независимых испытаниях
Число k0 (наступления события в независимых испытаниях, в каждом из которых вероятность появления события равна р) называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях k0 раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.
Наивероятнейшее число k0 определяют из двойного неравенства
причем:
а) если число np – q – дробное, то существует одно наивероятнейшее число k0;
б) если число np – q – целое, то существует два наивероятнейших числа, а именно: k 0 и k0 + 1;
в) если число np – целое, то наивероятнейшее число k0 = np.
79. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание.
80. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже.
|
|
|
81. Два равносильных противника играют в шахматы. Найти наивероятнейшее число выигрышей для любого шахматиста, если будет сыграно 2N результативных (без ничьих) партий.
Решение. Известно, что если произведение числа испытаний n на вероятность р появления события в одном испытании есть целое число, то наивероятнейшее число
k0 = np.
В рассматриваемой задаче число испытаний n равно числу сыгранных партий 2N; вероятность появления события равна вероятности выигрыша в одной партии, т. е. p = 1/2 (по условию противники равносильны).
Поскольку произведение 
– целое число, то искомое наивероятнейшее число k0 выигранных партий равно N.
82. Два стрелка стреляют по мишени. Вероятность промаха при одном выстреле для первого стрелка равна 0,2, а для второго — 0,4. Найти наивероятнейшее число залпов, при которых не будет ни одного попадания в мишень, если стрелки произведут 25 залпов.
83. Сколько надо произвести независимых испытаний с вероятностью появления события в каждом испытании, равной 0,4, чтобы наивероятнейшее число появлений события в этих испытаниях было равно 25?
84. Чему равна вероятность р наступления события в каждом из 49 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 30?
85. Батарея произвела шесть выстрелов по объекту. Вероятность попадания в объект при одном выстреле равна 0,3. Найти: а) наивероятнейшее число попаданий; б) вероятность наивероятнейшего числа попаданий; в) вероятность того, что объект будет разрушен, если для этого достаточно хотя бы двух попаданий.
Производящая функция
В предыдущих пунктах этой темы рассматривались испытания с одинаковыми вероятностями появления события; рассмотрим испытания, в которых вероятности появления события различны.
Пусть производится n независимых испытаний, причём в первом испытании вероятность появления события А равна р1, во втором – р2, …, в n -ом испытании – pn; вероятности непоявления события А соответственно равны q1, q2, …, qn; Pn(k) – вероятность появления события А в n испытаниях ровно k раз.
|
|
|
Производящей функцией вероятностей Pn(k) называют функцию, определяемую равенством
Вероятность Pn(k) того, что в n независимых испытаниях, в первом из которых вероятность появления события А равна p1, во втором p2 и т. д., событие А появится ровно k раз, равна коэффициенту при zk в разложении производящей функции по степеням z. Например, если n = 2, то
Здесь коэффициент p1 p2 при z2 равен вероятности Р2(2) того, что событие А появится ровно два раза в двух испытаниях; коэффициент 
при z1 равен вероятности Р2(1) того, что событие А появится ровно один раз; коэффициент при z0, т. е. свободный член q1q2 равен вероятности Р2(0) того, что событие А не появится ни одного раза.
Заметим, что если в различных испытаниях появляются различные события (в первом испытании событие А1, во втором событие А2 и т.д.), то изменяется лишь истолкование коэффициентов при различных степенях z. Например, в приведённом выше разложении коэффициент p1 p2 определяет вероятность появления двух событий А1 и А2.
86. Устройство состоит из трёх независимо работающих элементов. Вероятность безотказной работы элементов (за время t) соответственно равны: p1 = 0,7; p2 = 0,8; p3 = 0,9. Найти вероятности того, что за время t будут работать безотказно: а) все элементы; б) два элемента; в) один элемент; г) ни один из элементов.
87. Из двух орудий произведен залп по цели. Вероятность попадания в цель для первого орудия равна 0,8, для второго – 0,9. Найти вероятности следующих событий: а) два попадания в цель; б) одно попадание; в) ни одного попадания; г) не менее одного попадания.
88. Из трех орудий произведен залп по цели. Вероятность попадания в цель для первого орудия равна 0,8, для второго – 0,85, для третьего – 0,9. Найти вероятности следующих событий: а) три попадания в цель; б) два попадания; в) одно попадание; г) ни одного попадания; д) хотя бы одно попадание.
|
|
|
