Функция двух случайных аргументов

Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y и пишут

Z = j(X, Y).

Если X и Y – дискретные независимые случайные величины, то, для того чтобы найти распределение функции Z = X + Y, надо найти все возможные значения Z, для чего достаточно сложить каждое возможное значение X со всеми возможными значениями Y; вероятности найденных возможных значений Z равны произведениям вероятностей складываемых значений X и Y.

Если X и Y – непрерывные независимые случайные величины, то плотность распределений g(z) суммы Z = X+Y (при условии, что плотность распределения хотя бы одного из аргументов задана в интервале (–∞, ∞) одной формулой) может быть найдена по формуле

либо по равносильной формуле

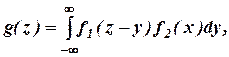
где f₁ и f₂ – плотности распределения аргументов; если возможные значения аргументов неотрицательны, то плотность распределения g(z) величины Z = X+Y находят по формуле

либо по равносильной формуле

В том случае, когда обе плотности f₁(x) и f₂(у) заданы на конечных интервалах, для отыскания плотности g(z) величины Z = X + Y целесообразно сначала найти функцию распределения G (z), а затем продифференцировать ее по z:

g(z) = G'(z).

Если X и Y – независимые случайные величины, заданные соответствующими плотностями распределения f₁(x) и f₂(у), то вероятность попадания случайной точки (X, Y) в область D равна двойному интегралу по этой области от произведения плотностей распределения:

 

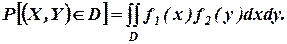
221. Дискретные независимые случайные величины X и Y заданы распределениями:

X			;	Y
p	0,3	0,7	P	0,6	0,4

Найти распределение случайной величины Z=X+Y.

Решение. Для того чтобы составить распределение величины Z=X + Y, надо найти все возможные значения Z и их вероятности.

Возможные значения Z есть суммы каждого возможного значения X со всеми возможными значениями Y:

z₁ = 1+2 = 3; z₂ = 1+4 = 5; z₃ = 3+2 = 5; z₄ = 3+4 = 7.

Найдем вероятности этих возможных значений. Для того чтобы Z = 3, достаточно, чтобы величина X приняла значение x₁ =l и величина Y – значение y₁=2. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,3 и 0,6. Так как аргументы X и Y независимы, то события Х = 1 и Y = 2 независимы и, следовательно, вероятность их совместного наступления (т. е. вероятность события Z = 3) по теореме умножения равна 0,3∙0,6=0.18.

Аналогично найдем:

p(Z = 1+4 = 5) = 0,3∙0,4=0,12;

p(Z = 3+2 = 5) = 0,7∙0,6=0,42;

p (Z = 3+4 = 7) = 0,7∙0,4=0,28.

Напишем искомое распределение, сложив предварительно вероятности несовместных событий Z = z₂ = 5, Z = z₃ = 5 (0,12+0,42 = 0,54):

Z
p	0,18	0,54	0,28

Контроль: 0,18 + 0,54 + 0,28=1.

 

222. Дискретные случайные величины X и Y заданы распределениями:

а)	X				,	Y			;
P	0,4	0,1	0,5	P	0,2	0,8
б)	X			,	Y			.
P	0,7	0,3	P	0,8	0,2

Найти распределение случайной величины Z = X + Y.

223. Независимые случайные величины X и Y заданы плотностями распределений:

f₁(x) = e^-x (0 ≤ x < ∞), f₂(y) = (1/2)e^-y/2 (0 ≤ y < ∞).

Найти композицию этих законов, т.е. плотность распределения случайной величины Z = X + Y.

224. Независимые нормально распределенные случайные величины X и Y заданы плотностями распределений:

f₁(x) = (1/ ) , f₂(x) = (1/ ) .

Доказать, что композиция этих законов, т.е. плотность распределения случайной величины Z = X + Y, также есть нормальный закон.

225. Заданы плотности распределений независимых равномерно распределенных случайных величин X и Y:

f₁(x)= 1/2 в интервале (0, 2), вне этого интервала f₁(x)= 0;

f₂(y)= 1/2 в интервале (0, 2), вне этого интервала f₂(y)= 0;

Найти функцию распределения и плотность распределения случайной величины Z=X+Y. Построить график плотности распределения g(z).

 

 

Тема 8. Система двух случайных величин

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: