Главная | Обратная связь | Поможем написать вашу работу!

Закон распределения двумерной случайной величины

Двумерной называют случайную величину (X, Y), возможные значения которой есть пары чисел (x, у). Составляющие X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.

Двумерную величину геометрически можно истолковать как случайную точку M (Х; Y) на плоскости xOy либо как случайный вектор OM.

Дискретной называют двумерную величину, составляющие которой дискретны.

Непрерывной называют двумерную величину, составляющие которой непрерывны.

Законом распределения вероятностей двумерной случайной величины называют соответствие между возможными значениями и их вероятностями.

Закон распределения дискретной двумерной случайной величины может быть задан: а) в виде таблицы с двойным входом, содержащей возможные значения и их вероятности; б) аналитически, например в виде функции распределения.

Функцией распределения вероятностей двумерной случайной величины называют функцию F(x, у), определяющую для каждой пары чисел (x, у) вероятность того, что X примет значение, меньшее x, и при этом Y примет значение, меньшее y:

F(x, у) = Р(Х < x, Y < y).

Геометрически это равенство можно истолковать так: F(х, у) есть вероятность того, что случайная точка (X, Y) попадет в бесконечный квадрант с вершиной (x,y), расположенный левее и ниже этой вершины.

Иногда вместо термина «функция распределения» используют термин «интегральная функция».

Функция распределения обладает следующими свойствами:

Свойство 1. Значения функции распределения удовлетворяют двойному неравенству

0 ≤ F (x, у) ≤ 1.

Свойство 2. Функция распределения есть неубывающая функция по каждому аргументу:

F(x₂, y) ≥ F(x₁, y), если x₂ > x₁,

F(x, y₂) ≥ F(x, y₁), если y₂ > y₁.

Свойство 3. Имеют место предельные соотношения:

1) F(–∞, y) = 0,

3) F(–∞, –∞) = 0,

2) F(x, –∞) = 0,

4) F(∞, ∞) = 1.

Свойство 4. а) При у =∞ функция распределения системы становится функцией распределения составляющей X:

F(x, ∞) = F₁(x).

б) При x = ∞ функция распределения системы становится функцией распределения составляющей Y:

F(∞, y) = F₂(y).

Используя функцию распределения, можно найти вероятность попадания случайной точки в прямоугольник x₁ < X < x₂, y₁ < Y < у₂:

P(x₁ < X < x₂, y₁ < Y < у₂) = [F(x₂, y₂) – F(x₁, y₂)] – [F(x₂, y₁) – F(x₁, y₁)].

Плотностью совместного распределения вероятностей (двумерной плотностью вероятности) непрерывной двумерной случайной величины называют вторую смешанную производную от функции распределения:

Иногда вместо термина «двумерная плотность вероятности» используют термин «дифференциальная функция системы».

Плотность совместного распределения можно рассматривать как предел отношения вероятности попадания случайной точки в прямоугольник со сторонами D x и D y к площади этого прямоугольника, когда обе его стороны стремятся к нулю; геометрически ее можно истолковать как поверхность, которую называют поверхностью распределения.

Зная плотность распределения, можно найти функцию распределения по формуле

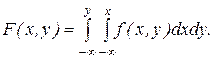
Вероятность попадания случайной точки (X, Y) в область D определяется равенством

Двумерная плотность вероятности обладает следующими свойствами:

Свойство 1. Двумерная плотность вероятности неотрицательна:

f(x,y) ≥ 0.

Свойство 2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности вероятности равен единице:

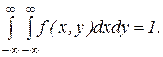
В частности, если все возможные значения (X, У) принадлежат конечной области D, то

226. Задано распределение вероятностей дискретной двумерной случайной величины:

Y	X

	0,17	0,13	0,25
	0,10	0,30	0,05

Найти законы распределения составляющих X и Y.

227. Задано распределение вероятностей дискретной двумерной случайной величины:

Y	X

2,3	0,05	0,12	0,08	0,04
2,7	0,09	0,30	0,11	0,21

Найти законы распределения составляющих.

228. Задана функция распределения двумерной случайной величины

Найти вероятность попадания случайной точки (X, Y) в прямоугольник, ограниченный прямыми x = 0, x = p/4, y = p/6, y = p/3.

229. Найти вероятность попадания случайной точки (X, Y) в прямоугольник, ограниченный прямыми x = 1, x = 2, y = 3, y = 5, если известна функция распределения

230. Задана функция распределения двумерной случайной величины

Найти двумерную плотность вероятности системы.

231. В круге x² + y² ≤ R² двумерная плотность вероятности ; вне круга f(x, y)= 0. Найти: а) постоянную C; б) вероятность попадания случайной точки (X, Y) в круг радиуса r = 1 с центром в начале координат, если R = 2.

232. В первом квадранте задана функция распределения системы двух случайных величин F(x, y) = 1 + 2^-^x – 2^-^y + 2^-^x-^y. Найти: а) двумерную плотность вероятности системы; б) вероятность попадания случайной точки (X, Y) в треугольник с вершинами A (1; 3), B (3; 3), C (2; 8).

8.2. Условные законы распределения вероятностей составляющих
дискретной двумерной случайной величины

Пусть составляющие X и Y дискретны и имеют соответственно следующие возможные значения: x₁, x₂, …, x_n; y₁, y₂, …, y_m.

Условным распределением составляющей X при Y=y_j (j сохраняет одно и то же значение при всех возможных значениях X) называют совокупность условных вероятностей

p(x₁|y_j), p(x₂|y_j), …, p(x_n|y_j).

Аналогично определяется условное распределение Y.

Условные вероятности составляющих X и Y вычисляют соответственно по формулам

Для контроля вычислений целесообразно убедиться, что сумма вероятностей условного распределения равна единице.

233. Задана дискретная двумерная случайная величина (X, Y):

Y	X
x₁=2	x₂=5	x₃=8
y₁=0,4	0,15	0,30	0,35
y₂=0,8	0,05	0,12	0,03

Найти: а) безусловные законы распределения составляющих; б) условный закон распределения составляющей X при условии, что составляющая Y приняла значение y₁ =0,4; в) условный закон распределения Y при условии, что X = x₂ =5.

234. Задана дискретная двумерная случайная величина (X, Y):

Y	X

	0,25	0,10
		0,32
	0,32	0,13

Найти: а) условный закон распределения X при условии, что Y =10; б) условный закон распределения Y при условии, что X =6.

8.3. Отыскание плотностей и условных законов распределения
составляющих непрерывной двумерной случайной величины

Плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей:

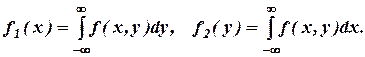
Здесь предполагается, что возможные значения каждой из составляющих принадлежат всей числовой оси; если же возможные значения принадлежат конечному интервалу, то в качестве пределов интегрирования принимают соответствующие конечные числа.

Условной плотностью распределения составляющей X при заданном значении Y = y называют отношение плотности совместного распределения системы к плотности распределения составляющей Y:

Аналогично определяется условная плотность распределения составляющей Y:

Если условные плотности распределения случайных величин X и Y равны их безусловным плотностям, то такие величины независимы.

Равномерным называют распределение двумерной непрерывной случайной величины (X, Y), если в области, которой принадлежат все возможные значения (x, у), плотность совместного распределения вероятностей сохраняет постоянное значение.

235. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y)

Найти: а) плотности распределения составляющих; б) условные плотности распределения, составляющих.

236. Плотность совместного распределения непрерывной двумерной случайной величины (X, Y)

Найти: а) постоянный множитель C; б) плотности распределения составляющих; в) условные плотности распределения составляющих.

237. Непрерывная двумерная случайная величина (X, У) распределена равномерно внутри прямоугольника с центром симметрии в начале координат и сторонами 2а и 2b, параллельными координатным осям. Найти: а) двумерную плотность вероятности системы; б) плотности распределения составляющих.

238. Непрерывная двумерная случайная величина (X, У) равномерно распределена внутри прямоугольного треугольника с вершинами O (0; 0), А (0; 8), В (8;0). Найти: а) двумерную плотность вероятности системы; б) плотности и условные плотности распределения составляющих.

8.4. Числовые характеристики непрерывной системы
двух случайных величин

Зная плотности распределения составляющих X и Y непрерывной двумерной случайной величины (X, У), можно найти их математические ожидания и дисперсии:

Иногда удобнее использовать формулы, содержащие двумерную плотность вероятности (двойные интегралы берутся по области возможных значений системы):

Начальным, моментом n_k,_s порядка k+s системы (X, Y) называют математическое ожидание произведения X^kY^s:

n_k,_s = M[X^kY^s].

В частности,

n_1,0 = M(X), n_0,1 = M(Y).

Центральным моментом m_k,_s порядка k+s системы (X, Y) называют математическое ожидание произведения отклонений соответственно k -й и s -й степеней:

m_{k, s} = M{[X – M(X)]^k ∙ [Y – M(Y)]^s}.

В частности,

m_1,0 =M[X – M(X)] = 0, m_0,1 = M[Y – M(Y)] = 0;

m_2,0 =M[X – M(X)]² = D(X), m_0,2 = M[Y – M(Y)]² = D(Y);

Корреляционным моментом m_xу системы (X, Y) называют центральный момент m_1,1 порядка 1 + 1:

m_xу = M{[X – M(X)] ∙ [Y – M(Y)]}.

Коэффициентом корреляции величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

r_xy = m_xy / (s_xs_y).

Коэффициент корреляции – безразмерная величина, причем | r_xy | ≤ 1. Коэффициент корреляции служит для оценки тесноты линейной связи между X и Y: чем ближе абсолютная величина коэффициента корреляции к единице, тем связь сильнее; чем ближе абсолютная величина коэффициента корреляции к нулю, тем связь слабее.

Коррелированными называют две случайные величины, если их корреляционный момент отличен от нуля.

Некоррелированными называют две случайные величины, если их корреляционный момент равен нулю.

Две коррелированные величины также и зависимы; если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя сделать вывод о независимости этих величин (для нормально распределенных величин из некоррелированности этих величин вытекает их независимость).

Для непрерывных величин X и Y корреляционный момент может быть найден по формулам:

239. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y):

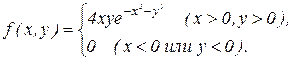
Найти: а) математические ожидания; б) дисперсии составляющих X и Y.

240. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y):

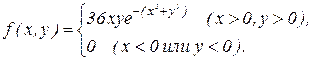
Найти математические ожидания и дисперсии составляющих.

241. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y): f(x, y) = 2 cosx cosy в квадрате 0 ≤ x ≤p/4, 0 ≤ y ≤p/4; вне квадрата f(x, y) = 0. Найти математические ожидания составляющих.

242. Доказать, что если двумерную плотность вероятности системы случайных величин (X, Y) можно представить в виде произведения двух функций, одна из которых зависит только от x, а другая – только от y, то величины X и Y независимы.

243. Доказать, что если X и Y связаны линейной зависимостью Y = aX + b, то абсолютная величина коэффициента корреляции равна единице.

Решение. По определению коэффициента корреляции,

r_xy = m_xy / (s_xs_y).

где

m_xу = M{[X – M(X)] ∙ [Y – M(Y)]}. (*)

Найдем математическое ожидание Y:

M(Y) = M[aX + b] = aM(X) + b. (**)

Подставив (**) в (*), после элементарных преобразований получим

m_xу = aM[X – M(X)]² = aD(X) = as²_x.

Учитывая, что

Y – M(Y) = (aX + b) – (aM(X) + b) = a[X – M(X)],

найдем дисперсию Y:

D(Y) = M[Y – M(Y)]² = a²M[X – M(X)]² = a²s²_x.

Отсюда s_y = |a|s_x. Следовательно, коэффициент корреляции

Если a > 0, то r_xy = 1; если a < 0, то r_xy = –1.

Итак, | r_xy | = 1, что и требовалось доказать.

⇐ Предыдущая 3 4 5 6 7 8 9 101112 Следующая ⇒

Воспользуйтесь поиском по сайту: