Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Стационарно связанные случайные функции




Стационарно связанными называют две случайные функции X(t) и Y(t), взаимная корреляционная функция которых зависит только от разности аргументов t = t2 – t1: Rxy = r(t).

Не всякие две стационарные функции стационарно связаны; с другой стороны, две нестационарные функции могут быть стационарно связанными.

 

283. Доказать, что для стационарных и стационарно связанных случайных функций X(t) и Y(t) абсолютная величина взаимной корреляционной функции не превышает среднего геометрического дисперсий этих функций:

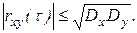
Указание. Использовать свойство 4 взаимной корреляционной функции.

 

284. Заданы две стационарные случайные функции: X(t) = cos(t + j) и Y(t) = sin(t + j), где j – случайная величина, распределенная равномерно а интервале (0,2p). Доказать, что заданные стационарные функции стационарно связаны.

285. Заданы случайные функции X(t) = Vcost – Usint, Y(t) = Ucost + Vsint, где U и V – некоррелированные случайные величины, причем их математические ожидания равны нулю, а дисперсии равны 5. Доказать, что заданные функции стационарны и стационарно связаны.

 

10.3. Корреляционная функция производной от стационарной
случайной функции

Корреляционная функция производной X'(t) = x дифференцируемой стационарной случайной функции X (t) равна второй производной от ее корреляционной функции, взятой со знаком минус:

 

286. Доказать, что если известна корреляционная функция kx(t) дифференцируемой стационарной случайной функции X (t), то корреляционная функция ее производной kx(t) = – k"x (t).

287. Доказать, что производные любого порядка (если они существуют) от стационарной случайной функции также стационарны.

288. Задана корреляционная функция стационарной случайной функции X(t). Найти: а) корреляционную функцию и дисперсию производной X'(t)=x; б) отношение дисперсий функции X (t) и ее производной.

289. Заданы математическое ожидание mx(t) =8 и корреляционная функция kx(t)=5e–|t|[cos2t + 0,5sin2|t|] нормальной стационарной случайной функции X(t). Найти вероятность того, что производная Y(t) = X'(t) заключена в интервале (0,10).

290. Заданы математическое ожидание mx =12 и корреляционная функция kx(t)=4e–|t|[cos2t + 0,5sin2|t|] нормальной стационарной случайно функции X(t). Найти вероятность того, что производная Y(t) = X'(t) принимает значения, большие, чем .

 

10.4. Корреляционная функция интеграла от стационарной
случайной функции

Корреляционную функцию и дисперсию интеграла от стационарной случайной функции находят соответственно по формулам:

291. Задана корреляционная функция kx(t) стационарной случайной функции X(t). Доказать, что корреляционная функция интеграла равна

Указание. При отыскании двойного интеграла 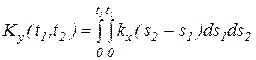перейти к новым переменным t = s2 – s1, x = s2 – s1. Начертить новую область интегрирования, ограниченную прямыми t = x, t = –x, t = x – 2t1, t = –x + 2t2, и выполнить интегрирование по x. Двойной интеграл по области OABD вычислить как разность двойных интегралов по областям ОАС и BDC. При интегрировании по области ODE переставить пределы интегрирования пот и перейти к новой переменной интегрирования t = - t (рис. 3).

 

292. Известна корреляционная функция kx(t) стационарной случайной функции X(t). Доказать, что дисперсия интеграла равна

293. Найти дисперсию интеграла , зная корреляционную функцию стационарной случайной функции X(t): а) kx(t) = 1/(1 + t2); б) kx(t) = =De–a|t| (a > 0); в) kx(t) = =De–a|t|(1 + a|t|).

294. Задана корреляционная функция kx(t)=10e-0,5|t|(1+0,5|t|). Найти отношение дисперсии случайной величины к дисперсии случайной функции X(t).

 

10.5. Взаимная корреляционная функция дифференцируемой
стационарной случайной функции и ее производных

Ниже предполагается, что t = t2 – t1.

Взаимные корреляционные функции стационарной случайной функции X(t) и ее производных выражаются формулами:

 

295. Доказать, что взаимная корреляционная функция дифференцируемой стационарной случайной функции X(t) и ее производной X'(t) = x равна первой производной от корреляционной функции kx(t), взятой со своим (противоположным) знаком, если индекс стоит на втором (первом) по порядку месте: а) ; б) .

296. Найти взаимные корреляционные функции стационарной случайной функции X(t) и ее производной, зная корреляционную функцию kx(t) = e–|t|(1+|t|).

297. Доказать, что взаимная корреляционная функция стационарной случайной функции X (t) и ее производной изменяет знак при перемене местами аргументов t1 и t2.

298. Найти корреляционную функцию случайной функции Y(t) = X(t) + X'(t) зная корреляционную, функцию kx(t) стационарной функции X(t).

299. Найти корреляционную функцию случайной функции Y(t) = X(t) + X'(t) зная корреляционную, функцию стационарной функции X(t).

 

 

Литература

 

1. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пос. для студентов вузов. Изд. 5-е стер. – М.: Высш. шк. 1999. – 400 с.

2. Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб. пос. для студентов вузов. Изд. 7-е стер. – М.: Высш. шк. 1999. – 479 с.

3. Севостьянов Б. А. и др. Сборник задач по теории вероятностей – М.: Наука, 1980 – 224 с.

4. Прохоров А. В. и др. Задачи по теории вероятностей: основные понятия. Предельные теоремы. Случайные процессы: Учеб. пос. – М.: Наука, 1986. – 328.с

5. Андрухаев Х. М. Сборник задач по теории вероятностей: Уч. пос. – М.: Просвещение, 1985. – 160 с.

6. Дедык И. С. и др. Сборник задач по теории вероятностей: Уч. пос. – Ленинград: ЛВИА им. Можайского, 1963. – 208 с.


ПРИЛОЖЕНИЯ

 

ПРИЛОЖЕНИЕ 1

Таблица значений функции

                     
0,0 0,3989                  
0,1                    
0,2                    
0,3                    
0,4                    
0,5                    
0,6                    
0,7                    
0,8                    
0,9                    
1,0 0,2420                  
1,1                    
1,2                    
1,3                   151 Я
1,4                    
1,5                    
1,6                    
1,7                    
1,8                    
1,9                    
2,0 0,0540                  
2,1                    
2,2                    
2,3                    
2,4                    
2,5                    
2,6                    
2,7                    
2,8                    
2,9                    
3,0 0,0044                  
3,1                    
3,2                    
3,3                    
3,4                    
3,5                    
3,6                    
3,7                    
3,8                    
3,9                    

Приложение 2

Таблица значений функции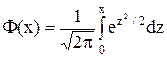

x F(x) x Ф(x) x Ф(x) x Ф(x)
0,00 0,0000 0,32 0,1255 0,64 0,2389 0,96 0,3315
0,01 0,0040 0,33 0,1293 0,65 0,2422 0,97  
0,02 0,0080 0,34 0,1331 0,66 0,2454 0,98 0,3365
0,03 0,0120 0,35 0,1368 0,67 0,2486 0,99 0,3389
  0,0160 0,36 0,1406 0,68 0,2517 1,00  
0,05 0,0199 0,37 0,1443 0,69 0,2549 1,01 0,3438
0,06 0,0239 0,38 0,1480 0,70 0,2580 1,02 0,3461
0,07 0,0279 0,39 0,1517 0,71 0,2611 1,03 0,3485
0,08 0,0319 0,40 0,1554 0,72 0,2642 1,04  
0,09 0,0359 0,41 0,1591 0,73 0,2673 1,05 0,3531
0,10 0,0398 0,42 0,1628 0,74 0,2703 1,06  
0,11 0,0438 0,43 0,1664 0,75 0,2734 1,07  
0,12 0,0478 0,44 0,1700 0,76 0,2764 1,08  
0,13 0,0517 0,45 0,1736 0,77 0,2794 1,09  
0,14 0,0557 0,46 0,1772 0,78 0,2823 1,10  
0,15 0,0596 0,47 0,1808 0,79   1,11  
0,16 0,0636 0,48 0,1844 0,80 0,2881 1,12 0,3686
0,17 0,0675 0,49   0,81 0,2910 1,13  
0,18 0,0714 0,50 0,1915 0,82 0,2939 1,14 0,3729
0,19 0,0753 0,51 0,1950 0,83 0,2967 1,15  
0,20 0,0793 0,52 0,1985 0,84 0,2995 1,16 0,3770
0,21 0,0832 0,53 0,2019 0,85 0,3023 1,17 0,3790
0,22 0,0871 0,54 0,2054 0,86 0,3051 1,18 0,3810
0,23 0,0910 0,55 0,2088 0,87 0,3078 1,19 0,3830
0,24 0,0948 0,56 0,2123 0,88 0,3106 1,20 0,3849
0,25 0,0987 0,57 0,2157 0,89 0,3133 1,21  
0,26 0,1026 0,58 0,2190 0,90 0,3159 1,22 0-3883
0,27 0,1064 0,59 0,2224 0,91 0,3186 1,23  
0,28 0,1103 0,60 0,2257 0,92 0,3212 1,24  
0,29 0,1141 0,61 0,2291 0,93 0,3238 1,25 0,3944
0,30 0,1179   0,2324 0,94 0,3264    
0,31 0,1217 0,63 0,2357 0,95 0,3289    
               
1,26 0,3962 1,59 0,4441 1,92 0,4726 2,50 0,4938
1,27 0,3980 1,60 0,4452 1,93 0,4732 2,52 0,4941
1,28 0,3997 1,61 0,4463 1,94 0,4738 2,54 0,4945
1,29 0,4015 1,62 0,4474 1,95 0,4744 2,56 0,4948
1,30 0,4032 1,63 0,4484 1,96 0,4750 2,58 0,4951
1,31 0,4049 1,64 0,4495 1,97 0,4756 2,60 0,4953
1,32 0,4066 1,65 0,4505 1,98 0,4761 2,62 0,4956
1,33 0,40,82 1,66 0,4515 1,99 0,4767 2,64 0,4959
1,34 0,4099 1,67 0,4525 2,00 0,4772 2,66 0,4961
1,35 0,4115 1,68 0,4535 2,02 0,4783 2,68 0,4963
1,36 0,4131 1,69 0,4545 2,04 0,4793 2,70 0,4965
1,37 0,4147 1,70 0,4554 2,06 0,4803 2,72 0,4967
1,38 0,4162 1,71 0,4564 2,08 0,4812 2,74 0,4969

 

Продолжение приложения 2

x Ф(x) x Ф(x) x Ф(x) x Ф(x)
1,39 0,4177 1,72 0,4573 2,10 0,4821 2,76 0,4971
1,40 0,4192 1,73 0,4582 2,12 0,4830 2,78 0,4973
1,41 0,4207 1,74 0,4591 2,14 0,4838 2,80 0,4974
1,42 0,4222 1,75 0,4599 2,16 0,4846 2,82 0,4976
1,43 0,4236 1,76 0,4608 2,18 0,4854 2,84 0,4977
1,44 0,4251 1,77 0,4616 2,20 0,4861 2,86 0,4979
1,45 0,4265 1,78 0,4625 2,22 0,4868 2,88 0,4980
1,46 0,4279 1,79 0,4633 2,24 0,4875 2,90 0,4981
1,47 0,4292 1,80 0,4641 2,26 0,4881 2,92 0,4982
1,48 0,4306 1,81 0,4649 2,28 0,4887 2,94 0,4984
1,49 0,4319 1,82 0,4656 2,30 0,4893 2,96 0,4985
1,50 0,4332 1,83 0,4664 2,32 0,4898 2,98 0,4986
1,51 0,4345 1,84 0,4671 2,34 0,4904 3,00 0,49865
1,52 0,4357 1,85 0,4678 2,36 0,4909 3,20 0,49931
1,53 0,4370 1,86 0,4686 2,38 0,4913 3,40 0,49966
1,54 0,4382 1,87 0,4693 2,40 0,4918 3,60 0,499841
1,55 0,4394 1,88 0,4699 2,42 0,4922 3,80 0,499928
1,56 0,4406 1,89 0,4706 2,44 0,4927 4,00 0,499968
1,57 0,4418 1,9 0,4713 2,46 0,4931 4,50 0,499997
1,58 0,4429 1,91 0,4719 2,48 0,4934 5,00 0,499997

 

Приложение 3

Таблица значений tg = t(g, n)

g n 0,95 0,99 0,999 g n 0,95 0,99 0,099
  2,78 4,60 8,61   2,093 2,86,1 3,883
  2,57 4,03 6,86   2,064 2,797 3,745
  2,45 3,71 5,96   2,045 2,756 3,659
  2,37 3,50 5,41   2,032 2,720 3,600
  2,31 3,36 5,04   2,023 2,708 3,558
  2,26 3,25 4,78   2,016 2,692 3,527
  2,23 3,17 4,59   2,009 2,679 3,502
  2,20 3,11 4,44   2,001 2,662 3,464
  2,18 3,06 4,32   1,996 2,649 3,439
  2,16 3,01 4,22   1,991 2,640 3,418
  2,15 2,98 4,14   1,987 2,633 3,403
  2,13 2,95 4,07   1,984 2,627 3,392
  2,12 2,92 4,02   1,980 2,617 3,374
  2,11 2,90 3,97 ∞ 1,960 2,576 3,291
  2,10 2,88 3,92        

Приложение 4

Таблица значений q = q(g, n)

g n 0,95 0,99 0,999 g n 0,95 0,99 0,999
  1,37 2,67 5,64   0,37 0,58 0,88
  1,09 2,01 3,88   0,32 0,49 0,73
  0,92 1,62 2,98   0,28 0,43 0,63
  0,80 1,38 2,42   0,26 0,38 0,56
  0,71 1,20 2,06   0,24 0,35 0,50
  0,65 1,08 1,80   0,22 0,32 6,46
  0,59 0,98 1,60   0,21 0,30 0,43
  0,55 0,90 1,45   0,188 0,269 0,38
  0,52 0,83 1,33   0,174 0,245 0,34
  0,48 0,78 1,23   0,161 0,226 0,31
  0,46 0,73 1,15   0,151 0,211 0,29
  0,44 0,70 1,07   0,143 0,198 0,27
  0,42 0,66 1,01   0,115 0,160 0,211
  0,40 0,63 0,96   0,099 0,136 0,185
  0,39 0,60 0,92   0,089 0,120 0,162

 

 

Приложение 5

Критические точки распределения c*

Число степеней свободы h Уровень значимости a
0,01 0,025 0,05 0,95 0,975 0,99
  6,6 5,0 3,8 0,0039 0,00098 0,00016
  9,2 7,4 6,0 0,103 0,051 0,020
  11,3 9,4 7,8 0,352 0,216 0,115
  13,3 11,1 9,5 0,711 0,484 0,297
  15,1 12,8 11,1 1,15 0,831 0,554
  16,8 14,4 12,6 1,64 1,24 0,872
  18,5 16,0 14,1 2,17 1,69 1,24
  20,1 17,5 15,5 2,73 2,18 1,65
  21,7 19,0 16,9 3,33 2,70 2,09
  23,2 20,5 18,3 3,94 3,25 2,56
  24,7 21,9 19,7 4,57 3,82 3,05
  26,2 23,3 21,0 5,23 4,40 3,57
  27,7 24,7 22,4 5,89 5,01 4,11
  29,1 26,1 23,7 6,57 5,63 4,66
  30,6 27,5 25,0 7,26 6,26 5,23
  32,0 28,8 26,3 7,96 6,91 5,81
  33,4 30,2 27,6 8,67 7,56 6,41
  34,8 31,5 28,9 9,39 8,23 7,01
  36,2 32,9 30,1 10,1 8,91 7,63
  37,6 34,2 31,4 10,9 9,59 8,26
  38,9 35,5 32,7 11,6 10,3 8,90
  40,3 36,8 33,9 12,3 11,0 9,54
  41,6 38,1 35,2 13,1 11,7 10,2
  43,0 39,4 36,4 13,8 12,4 10,9
  44,3 40,6 37,7 14,6 13,1 11,5
  45,6 41,9 38,9 15,4 13,8 12,2

Продолжение приложения 5

Число степеней свободы h Уровень значимости a
0,01 0,025 0,05 0,95 0,975 0,99
  47,0 43,2 40,1 16,2 14,6 12,9
  48,3 44,5 41,3 16,9 15,3 13,6
  49,6 45,7 42,6 17,7 16,0 14,3
  50,9 47,0 43,8 18,5 16,8 15,0

 

 

Приложение 6

Критические точки распределения Стьюдента

Число степеней свободы k Уровень значимости a (двусторонняя критическая область)
0,10 0,05 0,02 0,01 0,002 0,001
  6,31 12,7 31,82 63,7 318,3 637,0
  2,92 4,30 6,97 9,92 22,33 31,6
  2,35 3,18 4,54 5,84 10,22 12,9
  2,13 2,78 3,75 4,60 7,17 8,61
  2,01 2,57 3,37 4,03 5,89 6,86
  1,94 2,45 3,14 3,71 5,21 5,96
  1,89 2,36 3,00 3,50 4,79 5,40
  1,86 2,31 2,90 3,36 4,50 5,04
  1,83 2,26 2,82 3,25 4,30 4,78
  1,81 2,23 2,76 3,17 4,14 4,59
  1,80 2,20 2,72 3,11 4,03 4,44
  1,78 2,18 2,68 3,05 3,93 4,32
  1,77 2,16 2,65 3,01 3,85 4,22
  1,76 2,14 2,62 2,98 3,79 4,14
  1,75 2,13 2,60 2,95 3,73 4,07
  1,75 2,12 2,58 2,92 3,69 4,01
  1,74 2,11 2,57 2,90 3,65 3,95
  1,73 2,10 2,55 2,88 3,61 3,92
  1,73 2,09 2,54 2,86 3,58 3,88
  1,73 2,09 2,53 2,85 3,55 3,85
  1,72 2,08 2,52 2,83 3,53 3,82
  1,72 2,07 2,51 2,82 3,51 3,79
  1,71 2,07 2,50 2,81 3,49 3,77
  1,71 2,06 2,49 2,80 3,47 3,74
  1,71 2,06 2,49 2,79 3,45 3,72
  1,71 2,06 2,48 2,78 3,44 3,71
  1,71 2,05 2,47 2,77 3,42 3,69
  1,70 2,05 2,46 2,76 3,40 3,66
  1,70 2,05 2,46 2,76 3,40 3,66
  1,70 2,04 2,46 2,75 3,39 3,65
  1,68 2,02 2,42 2,70 3,31 3,55
6O 1,67 2,00 2,39 2,66 3,23 3,46
  1,66 1,98 2,36 2,62 3,17 3,37
∞ 1,64 1,96 2,33 2,58 3,09 3,29
  0,05 0,025 0,01 0,005 0,001 0,0005
Уровень значимости a (односторонняя критическая область)

Приложение 7

 

Критические точки распределения F Фишера – Снедекора

(k1 – число степеней свободы большей дисперсии)

(k2 – число степеней свободы меньшей дисперсии)

Уровень значимости a = 0,01

k1 k2                        
        5G25                
  98,49 99,01 90,17 99,25 99,33 99,30 99,34 99,36 99,36 99,40 99,41 99,42
  34,12 30,81 29,46 28,71 28,24 27,91 27,67 27,49 27,34 27,23 27,13 27,05
  21,20 18,00 16,69 15,98 15,52 15,21 14,98 14,80 14,66 14,54 14,45 14,37
  16,26 13,27 12,06 11,39 10,97 10,67 10,45 10,27 10,15 10,05 9,96 9,89
  13,74 10,92 9,78 9,15 8,75 8,47 8,26 8,10 7,98 7,87 7,79 7,72
  12,25 9,55 8,45 7,85 7,46 7,19 7,00 6,84 6,71 6,62 6,54 6,47
  11,26 8,65 7,59 7,01 6,63 6,37 6,19 6,03 5,91 5,82 5,74 5,67
  10,56 8,02 6,99 6,42 6,06 5,80 5,62 5,47 5,35 5,26 5,18 5,11
  10,04 7,56 6,55 5,99 5,64 5,39 5,21 5,06 4,95 4,85 4,78 4,71
  9,86 7,20 6,22 5,67 5,32 5,07 4,88 4,74 4,63 4,54 4,46 4,40
  9,33 6,93 5,95 5,41 5,06 4,82 4,65 4,50 4,39 4,30 4,22 4,16
  9,07 6,70 5,74 5,20 4,86 4,62 4,44 4,30 4,19 4,10 4,02 3,96
  8,86 6,51 5,56 5,03 4,69 4,46 4,28 4,14 4,03 3,94 3,86 3,80
  8,68 6,36 5,42 4,89 4,56 4,32 4,14 4,00 3,89 3,80 3,73 3,67
  8,53 6,23 5,29 4,77 4,44 4,20 4,03 3,89 3,78 3,69 3,61 3,55
  8,40 6,11 5,18 4,67 4,34 4,10 3,93 3,79 3,68 3,59 3,52 3,45

 

Уровень значимости a = 0,05

k1 k2               в        
                         
  18,51 19,00 19,16 19,25 19,30 19,33 19,36 19,37 19,38 19,39 19,40 19,41
  10,13 9,55 9,28 9,12 9,01 8,94 8,88 8,84 8,81 8,78 8,76 8,74
  7,71 6,94 6,59 6,39 6,26 6,16 6,09 6,04 6,00 5,96 5,93 5,91
  6,61 5,79 5,41 5,19 5;05 4,95 4,88 4,82 4,78 4,74 4,70 4,68
  5,99 5,14 4,76 4,53 4,39 4,28 4,21 4,15 4,10 4,06 4,03 4,00
  5,59 4,74 4,35 4,12 3,97 3,87 3,79 3,73 3,68 3,63 3,60 3,57
  5,32 4,46 4,07 3,84 3,69 3,58 3,50 3,44 3,39 3,34 3,31 3,28
  5,12 4,26 3,86 3,63 3,48 3,37 3,29 3,23 3,18 3,13 3,10 3,07
  4,96 4,10 3,71 3,48 3,33 3,22 3,14 3,07 3,02 2,97 2,94 2,91
  4,84 3,98 3,59 3,36 3,20 3,09 3,01 2,95 2,90 2,86 2,82 2,79
  4,75 3,88 3,49 3,26 3,11 3,00 2,92 2,85 2,80 2,76 2,72 2,69
  4,67 3,80 3,41 3,18 3,02 2,92 2,84 2,77 2,72 2,67 2,63 2,60
  4,60 3,74 3,34 3,11 2,96 2,85 2,77 2,70 2,65 2,60 2,56 2,53
  4,54 3,68 3,29 3,06 2,90 2,79 2,70 2,64 2,59 2,55 2,51 2,48
  4,49 3,63 3,24 3,01 2,85 2,74 2,66 2,59 2,54 2,49 2,45 2,42
  4,45 3,59 3,20 2,% 2,81 2,70 2,62 2,55 2,50 2,45 2,41 2,38

Приложение 8

 

Критические точки распределения Кочрена

(k – число степеней свободы, l – количество выборок)

Уровень значимости a = 0,01

k l              
  0,9999 0,9950 0,9794 0,9586 0,9373 0,9172 0,8988
               
               
  0,9279 0,7885 0,6957 0,6329 0,5875 0,5531 0,5259
               
               
  0,7945 0,6152 0,5209 0,4627 0,4226 0,3932 0,3704
               
               
  0,6528 0,4751 0,3919 0,3428 0,3099 0,2861 0,2680
               
               
  0,4247 0,2871 0,2295 0,1970 0,1759 0,1608 0,1495
               
               
  0,2151 0,1371 0,1069 0,0902 0,0796 0,0722 0,0668
         
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...