 |
Глазовский государственный педагогический институт
|
|
|
|
Федеральное агентство по образованию
государственное образовательное учреждение
высшего профессионального образования
Глазовский государственный педагогический институт
им. В. Г. Короленко
Линейная алгебра
и аналитическая геометрия
Пособие
к практическим занятиям
для студентов факультета
социальных и информационных технологий
Глазов 2005
ББК
Линейная алгебра и аналитическая геометрия: Пособие к практическим занятиям. – Глазов, 2005. – 102 с.
Составители: кандидат физ. -мат. наук, доцент Л. Т. Крежевских, старший преподаватель кафедры алгебры, геометрии, теории и методики обучения математике И. Л. Мирошниченко
Рецензент: кандидат физ. -мат. наук, доцент кафедры математического анализа А. Д. Лумпов
Пособие содержит методические рекомендации по подготовке к 16 практическим занятиям по линейной алгебре и аналитической геометрии для студентов первого курса факультета социальных и информационных технологий, обучающихся по специальностям «030100 – информатика», «030100. 00 – информатика с дополнительной специальностью».
В каждом занятии приведена литература для самостоятельного изучения темы, контрольные вопросы и задания, типовые задачи с решениями, задачи для упражнений, для самостоятельного решения и задание на дом.
© Глазовский государственный педагогический институт, 2005
Введение
Раздел «Линейная алгебра и аналитическая геометрия» является составной частью курса «Математика» для студентов факультета социальных и информационных технологий, обучающихся по специальности «Информатика». Длительность изучения раздела – один семестр.
|
|
|
Данное пособие содержит методические рекомендации по подготовке к 16 практическим занятиям по линейной алгебре и аналитической геометрии. Несмотря на то, что основным источником теоретических сведений по каждой теме являются лекции, в начале каждого занятия указывается, какой основной литературой можно воспользоваться при самостоятельном изучении темы (в квадратных скобках указан номер соответствующего источника в списке основной литературы). Список основной и дополнительной литературы приводится в конце пособия.
Структура каждого занятия такова, что пособием можно пользоваться и при подготовке к практическим занятиям (как студентам, так и преподавателям), и на практических занятиях, и при самостоятельном изучении материала, и при подготовке к зачету.
Последовательность работы с данным пособием такова:
1. Выполнить в тетради домашнее задание, содержащееся в пункте V предыдущего занятия.
2. Изучить теорию по новой теме по лекциям или учебникам, указанным в начале занятия по данной теме, выучить необходимые определения и формулы, формулировки свойств и теорем.
3. Ответить на контрольные вопросы и выполнить задания из пункта I.
4. Внимательно прочитать и постараться понять решения типовых задач, приведенные в пункте II. Если в процессе работы над пунктами I и II возникли вопросы, их нужно выяснить с преподавателем на ближайшем практическом или индивидуальном занятии.
5. Основным видом работы на практическом занятии является решение задач из пункта III.
В пункте IV приведены более сложные задачи, которые студент может решать самостоятельно, а преподаватель – использовать по своему усмотрению.
В конце каждого практического занятия дается задание на дом, которое содержится в пункте V.
Последнее (шестнадцатое) занятие может быть вынесено преподавателем на самостоятельное изучение студентами. Для контроля за самостоятельной работой студентов по этой теме преподаватель может дать индивидуальную домашнюю контрольную работу, в которую включить типовые задачи на определение вида поверхности по ее каноническому уравнению и построение изображения этой поверхности. При этом количество вариантов желательно увеличить до количества студентов в группе.
|
|
|
Занятие 1
Тема: «Матрицы и действия над ними»
Литература для самостоятельного изучения темы: [1], гл. VII, VIII; [2], разд. I, гл. 2; [3], гл. 3; [4], гл. 3; [5], гл. V; [6], гл. VI; [7], гл. 1; [8], гл. 1; [9], гл. 10.
I. Контрольные вопросы и задания
1. Дайте определение матрицы размера m´ n.
2. Какие матрицы называются равными?
3. Дайте определения квадратной матрицы и ее порядка.
4. Дайте определения матрицы-строки и матрицы-столбца.
5. Перечислите элементы матрицы  составляющие:
составляющие:
а) главную диагональ; б) побочную диагональ.
6. Какая матрица называется диагональной?
7. Какая матрица называется единичной?
8. Дайте определение треугольной матрицы. Какая из следующих матриц является треугольной:
 ,
, 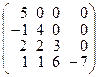 ,
,  ,
,  ?
?
9. Дайте определение транспонирования матрицы.
10. Найдите матрицу А – 3В, если
 ,
,  .
.
11. Можно ли найти произведение матриц  и
и  ?
?
12. Сколько строк и столбцов будет иметь матрица  , если матрица А имеет 5 строк и 2 столбца, а матрица В – 2 строки и 7 столбцов?
, если матрица А имеет 5 строк и 2 столбца, а матрица В – 2 строки и 7 столбцов?
13. Любые ли две матрицы являются коммутирующими?
14. Дайте определение матрицы, обратной данной матрице А.
15. Какая матрица называется обратимой?
16. Сформулируйте свойства операций над матрицами (14 свойств).
17. Какие преобразования матриц называют элементарными?
|
|
|


