 |
III. Задачи для упражнений. Занятие 5. Тема: «Векторы. Линейные операции над векторами». I. Контрольные вопросы и задания
|
|
|
|
III. Задачи для упражнений
1. Решите системы уравнений методом Гаусса:
а)  б)
б) 
в) 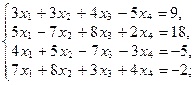 г)
г) 
2. Решите системы уравнений матричным методом:
а)  б)
б) 
3. Решите системы уравнений по формулам Крамера:
а) 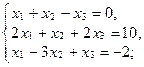 б)
б) 
в) 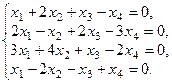
4. Найдите те значения параметра l, при которых система уравнений 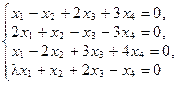 имеет только нулевое решение.
имеет только нулевое решение.
IV. Задачи для самостоятельного решения
1. Решите системы уравнений:
а) 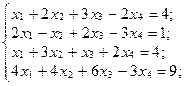 б)
б) 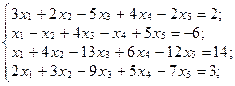
в) 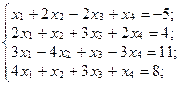 г)
г) 
V. Задание на дом
1. Решите системы уравнений методом Гаусса:
а)  б)
б) 
2. Решите системы уравнений двумя способами (матричным методом и по формулам Крамера):
а)  б)
б)  в)
в) 
3. Определите, при каких значениях l следующая система уравнений совместна: 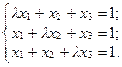
Найдите ее общее решение в тех случаях, когда она совместна. Существуют ли такие значения l, при которых система имеет единственное решение?
Занятие 5
Тема: «Векторы. Линейные операции над векторами»
Литература для самостоятельного изучения темы: [1], гл. II; [2], разд. I, гл. 2; [3], гл. 1; [4], гл. 2; [5], гл. I; [6], гл. I; [7], гл. 3; [8], гл. 3; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Дайте определения вектора, нулевого вектора.
2. Какие векторы 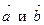 называются коллинеарными?
называются коллинеарными?
3. Какие векторы  называются компланарными?
называются компланарными?
4. Дайте определения сонаправленных, противоположно направленных векторов.
5. Дайте определение длины вектора.
6. Какие векторы называются равными?
7. Какие векторы называются противоположными?
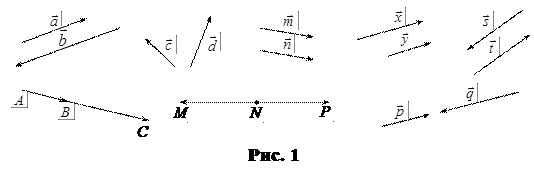 |
8. Назовите пары равных, противоположных, сонаправленных, противоположно направленных, коллинеарных векторов (рис. 1):
|
|
|
9. Дайте определение линейных операций над векторами.
10. Постройте сумму двух векторов, пользуясь правилом треугольника (рис. 2):

11. Запишите в буквенном виде правило треугольника для точек M, N и P. Сколькими способами можно это сделать?
 |
12. Постройте сумму двух векторов, пользуясь правилом параллелограмма (рис. 3):
13. Какие векторы можно складывать по правилу:
а) треугольника; б) параллелограмма?
14. Сформулируйте свойства сложения векторов.
15. Дайте определение суммы трех векторов, n векторов.
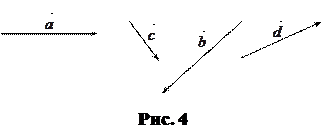 |
16. Найдите сумму векторов
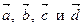 , пользуясь правилом многоугольника (рис. 4):
, пользуясь правилом многоугольника (рис. 4):
 |
17. Дайте определение разности двух векторов
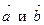 .
.
18. Постройте разность векторов 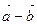 (рис. 5):
(рис. 5):
19. Дайте определение произведения вектора  на действительное число a.
на действительное число a.
20. На плоскости дан вектор  (рис. 6). Постройте вектор
(рис. 6). Постройте вектор  , если:
, если:
 а)
а) 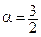 ; б)
; б)  .
.
21. Сформулируйте свойства умножения вектора на число.
22. Сформулируйте теорему о коллинеарных векторах.
23. Сформулируйте теорему о компланарных векторах.
II. Типовые задачи с решениями
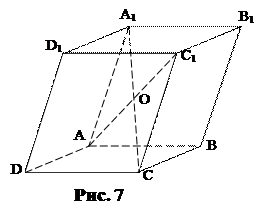 Задача 1. Дан произвольный параллелепипед
Задача 1. Дан произвольный параллелепипед 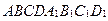 , О – его центр. Не выполняя дополнительных построений, найдите вектор
, О – его центр. Не выполняя дополнительных построений, найдите вектор 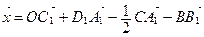 .
.
Решение. Так как  (рис. 7), то
(рис. 7), то 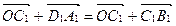 . По правилу треугольника
. По правилу треугольника  следовательно,
следовательно,  . Так как
. Так как  то
то  (по правилу нахождения разности векторов).
(по правилу нахождения разности векторов).
Наконец, 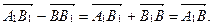
Ответ: 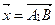 .
.
 Задача 2. В треугольнике АВС медианы
Задача 2. В треугольнике АВС медианы 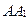 ,
,  ,
,  пересекаются в точке М. Выразите вектор
пересекаются в точке М. Выразите вектор  через векторы
через векторы 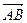 и
и 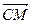 .
.
Решение. 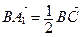 (рис. 8),
(рис. 8),  .
.
Так как  , а
, а  , то
, то 
Ответ: 
 Задача 3. В треугольнике АВС точки М и Р – середины сторон АС и ВС соответственно. Докажите, что
Задача 3. В треугольнике АВС точки М и Р – середины сторон АС и ВС соответственно. Докажите, что 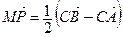 .
.
Решение. По правилу нахождения разности 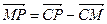 (рис. 9). Так как М и Р – середины сторон АС и ВС,
(рис. 9). Так как М и Р – середины сторон АС и ВС,  и
и 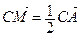 . Поэтому
. Поэтому  .
.
Задача 4. Точки P и Q – середины отрезков AB и CD соответственно. Докажите, что середины отрезков AС, BD и PQ лежат на одной прямой.
Решение. Пусть M, L и K – середины отрезков AС, BD и PQ соответственно (рис. 10). Чтобы доказать, что точки M, L и K лежат на одной прямой, докажем, что 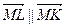 .
.
|
|
|
По правилу многоугольника
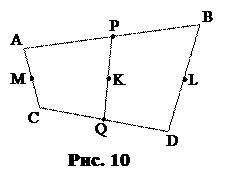

 .
.
Так как векторы 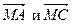 , а также векторы
, а также векторы  противоположны, то
противоположны, то 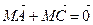 и
и  , поэтому
, поэтому  , откуда
, откуда  . Учитывая, что
. Учитывая, что 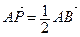 и
и  , получим:
, получим:
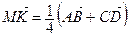 . (1)
. (1)
По правилу многоугольника

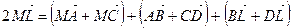 ;
;
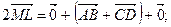
 , откуда
, откуда
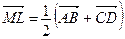 . (2)
. (2)
Выразим  из равенства (1)и подставим в равенство (2):
из равенства (1)и подставим в равенство (2):
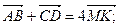

Из определения произведения вектора  на число 2 следует, что
на число 2 следует, что 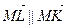 .
.
Замечание. Из векторного равенства 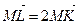 следует, что точка К является серединой отрезка ML.
следует, что точка К является серединой отрезка ML.
|
|
|


