 |
III. Задачи для упражнений. IV. Задачи для самостоятельного решения. V. Задание на дом. Занятие 6. Тема: «Базис. Координаты вектора в данном базисе»
|
|
|
|
III. Задачи для упражнений
1. 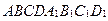 – произвольный параллелепипед, О – его центр, М – середина
– произвольный параллелепипед, О – его центр, М – середина 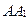 , Р – середина
, Р – середина  . а) Докажите, что
. а) Докажите, что 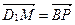 . б) Не выполняя дополнительных построений, найдите вектор
. б) Не выполняя дополнительных построений, найдите вектор 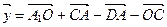 .
.
2. М – точка пересечения медиан 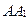 ,
,  и
и  треугольника АВС. Выразите вектор
треугольника АВС. Выразите вектор  через векторы
через векторы  .
.
3. ABCD – произвольный тетраэдр, Е – середина ребра BD. Выразите вектор  через векторы
через векторы  .
.
4. Докажите, что если 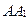 – медиана треугольника АВС, то
– медиана треугольника АВС, то 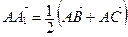 .
.
5. Докажите, что четырехугольник ABCD является параллелограммом тогда и только тогда, когда  .
.
6. Докажите векторным методом, что средняя линия треугольника параллельна основанию и равна его половине.
7. Докажите, что если A, B, C, D, E и F – середины сторон произвольного шестиугольника, то  .
.
IV. Задачи для самостоятельного решения
1. Даны векторы  . Постройте вектор
. Постройте вектор 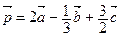 . Рассмотрите два случая: а)
. Рассмотрите два случая: а)  ; б) векторы
; б) векторы  попарно неколлинеарны.
попарно неколлинеарны.
2. ABCD – произвольный тетраэдр, М – середина ребра AD, N – середина ребра ВС. Выразите вектор  через векторы
через векторы  .
.
3. Векторы 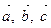 соединяют вершину пирамиды с вершинами ее основания. Векторы
соединяют вершину пирамиды с вершинами ее основания. Векторы 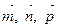 соединяют ту же вершину с серединами противоположных ребер. Докажите, что
соединяют ту же вершину с серединами противоположных ребер. Докажите, что 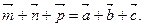
4. В плоскости взяты три точки А, В, М. На отрезке АВ взята точка С такая, что  . Выразите вектор
. Выразите вектор  через векторы
через векторы 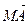 и
и 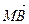 .
.
5. Докажите векторным методом, что если М – точка пересечения медиан треугольника АВС, то 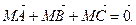
V. Задание на дом
1. 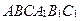 – произвольная треугольная призма, Р – середина ребра
– произвольная треугольная призма, Р – середина ребра 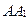 . Не выполняя дополнительных построений, найдите вектор
. Не выполняя дополнительных построений, найдите вектор 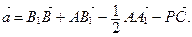
2. ABCD – параллелограмм, О – точка пересечения его диагоналей, Е – середина стороны AD. Выразите вектор  через векторы
через векторы 
3. Дан треугольник АВС и произвольная точка О пространства, М – точка пересечения медиан треугольника АВС. Докажите, что  .
.
|
|
|
4. Докажите векторным методом, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Занятие 6
Тема: «Базис. Координаты вектора в данном базисе»
Литература для самостоятельного изучения темы: [1], гл. II; [2], разд. I, гл. 2; [3], гл. 2; [4], гл. 2; [5], гл. I; [6], гл. I; [7], гл. 3; [8], гл. 3; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Дайте определение линейной комбинации векторов. Приведите пример линейной комбинации векторов.
2. Дайте определение базиса и ортонормированного базиса на плоскости и в пространстве.
3. Будут ли векторы  образовывать базис на плоскости и почему?
образовывать базис на плоскости и почему?
4. Будут ли векторы 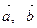 и
и  образовывать базис в пространстве и почему?
образовывать базис в пространстве и почему?
5. Дайте определение координат вектора в данном базисе.
6. Найдите координаты векторов:
а)  в базисе
в базисе  ;
;
б)  в базисе
в базисе 
7. Как выражается вектор  через базисные векторы
через базисные векторы  если он имеет в этом базисе следующие координаты:
если он имеет в этом базисе следующие координаты: 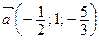 ?
?
8. Чему равны координаты суммы векторов, разности двух векторов, произведения вектора на число, линейной комбинации векторов?
9. Даны векторы  Найдите координаты следующих векторов:
Найдите координаты следующих векторов: 
10. Сформулируйте условие равенства двух векторов, заданных своими координатами.
11. Сформулируйте условие коллинеарности двух векторов, заданных своими координатами.
12. Выясните, коллинеарны ли следующие пары векторов:
а) 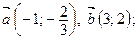
б) 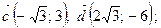
в) 
г) 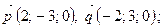
д) 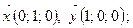
е) 
II. Типовые задачи с решениями
Задача 1. Даны три вектора 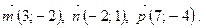 Определите координаты вектора
Определите координаты вектора  в базисе
в базисе 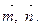
Решение. Первый способ. Пусть векторы 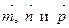 заданы в базисе
заданы в базисе  . Тогда их можно представить следующим образом:
. Тогда их можно представить следующим образом:

Обозначим через x, y координаты вектора  в базисе
в базисе 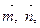 тогда
тогда 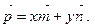 Подставляя в это равенство выражения векторов
Подставляя в это равенство выражения векторов 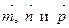 через базисные векторы
через базисные векторы 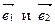 , получим:
, получим:  или
или  В левой части этого равенства стоит вектор с координатами
В левой части этого равенства стоит вектор с координатами  , в правой – вектор с координатами
, в правой – вектор с координатами  Применяя условие равенства двух векторов в координатах, получим систему:
Применяя условие равенства двух векторов в координатах, получим систему: 
|
|
|
Решая эту систему, найдем x = 1, y = – 2.
Ответ: 
Второй способ. Обозначим через x, y координаты вектора  в базисе
в базисе 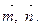 Тогда
Тогда 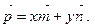
Учитывая, что каждая координата линейной комбинации двух векторов равна линейной комбинации соответствующих координат этих векторов, получим систему:
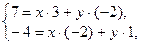 т. е.
т. е. 
Решая эту систему, найдем x = 1, y = – 2.
Ответ: 
 Задача 2. ABCD – параллелограмм, Е – середина стороны ВС, О – точка пересечения диагоналей AC и BD. Найдите координаты векторов
Задача 2. ABCD – параллелограмм, Е – середина стороны ВС, О – точка пересечения диагоналей AC и BD. Найдите координаты векторов  в базисе
в базисе 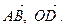
Решение. Так как 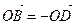 (рис. 11), то
(рис. 11), то  , следовательно,
, следовательно,  .
.



Ответ:  ,
, 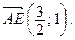
Задача 3. В треугольной призме  Р – середина ребра ВС, М – центр тяжести основания ABC. Найдите координаты вектора
Р – середина ребра ВС, М – центр тяжести основания ABC. Найдите координаты вектора  в базисе
в базисе 
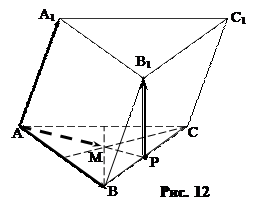 Решение. По правилу треугольника
Решение. По правилу треугольника  (рис. 12). Так как
(рис. 12). Так как 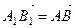 , то
, то 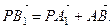
 По свойству центра тяжести треугольника
По свойству центра тяжести треугольника 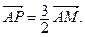 Тогда
Тогда 
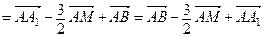
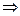
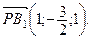
Ответ: 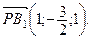
Задача 4. Даны векторы 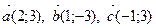 . При каком значении m векторы
. При каком значении m векторы  коллинеарны?
коллинеарны?
Решение. Найдем координаты векторов  :
:
 т. е.
т. е. 
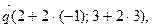 т. е.
т. е.  Для того, чтобы векторы
Для того, чтобы векторы  были коллинеарны, необходимо и достаточно, чтобы первая координата вектора
были коллинеарны, необходимо и достаточно, чтобы первая координата вектора  также была равна 0, т. е.
также была равна 0, т. е. 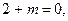 откуда
откуда 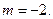
Ответ:  при
при 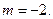
|
|
|


