 |
III. Задачи для упражнений. IV. Задачи для самостоятельного решения. V. Задание на дом. Занятие 9. Тема: «Векторное и смешанное произведения векторов»
|
|
|
|
III. Задачи для упражнений
1. Даны три вершины параллелограмма ABCD:  . Найдите координаты четвертой вершины и точки О пересечения диагоналей.
. Найдите координаты четвертой вершины и точки О пересечения диагоналей.
2. Докажите, что точки  лежат на одной прямой. Какая из этих точек лежит между двумя другими?
лежат на одной прямой. Какая из этих точек лежит между двумя другими?
3. Отрезок прямой, ограниченный точками  и
и 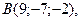 разделен точками C, D, E, F на пять равных частей. Найдите координаты этих точек.
разделен точками C, D, E, F на пять равных частей. Найдите координаты этих точек.
4. Докажите, что точки  и
и  являются вершинами квадрата.
являются вершинами квадрата.
5. Даны координаты двух вершин 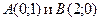 равностороннего треугольника. Найдите координаты третьей вершины.
равностороннего треугольника. Найдите координаты третьей вершины.
6. Даны две точки  на оси абсцисс найдите такую точку Р, чтобы угол MPN был прямым.
на оси абсцисс найдите такую точку Р, чтобы угол MPN был прямым.
IV. Задачи для самостоятельного решения
1. Определите, есть ли тупой угол среди внутренних углов треугольника с вершинами 


2. Середины сторон треугольника АВС находятся в точках  . Найдите координаты его вершин.
. Найдите координаты его вершин.
3. Вершины треугольника находятся в точках  . Найдите длину биссектрисы его внутреннего угла при вершине А.
. Найдите длину биссектрисы его внутреннего угла при вершине А.
4. Даны координаты двух смежных вершин квадрата ABCD: 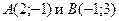 . Найдите координаты остальных вершин.
. Найдите координаты остальных вершин.
5. На прямой, проходящей через точки  найдите точку С, лежащую в плоскости а) Oxy; б) Oxz; в) Oyz.
найдите точку С, лежащую в плоскости а) Oxy; б) Oxz; в) Oyz.
6. Точки 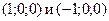 являются вершинами правильного тетраэдра, основание которого лежит в плоскости Oxy. Найдите координаты остальных вершин.
являются вершинами правильного тетраэдра, основание которого лежит в плоскости Oxy. Найдите координаты остальных вершин.
V. Задание на дом
1. Докажите, что точки 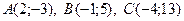 лежат на одной прямой.
лежат на одной прямой.
2. N – середина отрезка АВ, Р – середина отрезка NB. Найдите, в каком отношении точка А делит направленный отрезок  .
.
3. Докажите, что четырехугольник ABCD является трапецией (а не параллелограммом), и найдите длину ее средней линии, если 
4. На оси Ox найдите точку В, расстояние от которой до точки 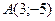 равно
равно  .
.
5. Даны две противоположные вершины квадрата 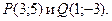 Вычислите его площадь.
Вычислите его площадь.
|
|
|
Занятие 9
Тема: «Векторное и смешанное произведения векторов»
Литература для самостоятельного изучения темы: [2], разд. I, гл. 2; [3], гл. 2; [4], гл. 2, 3; [5], гл. I; [6], гл. I; [7], гл. 3; [8], гл. 3; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Дайте определение векторного произведения двух векторов.
2. Векторы  и
и 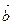 образуют угол
образуют угол  . Зная, что
. Зная, что  , вычислите
, вычислите  .
.
3. Чему равно векторное произведение векторов  и
и  ?
?
4. Пусть  . В каких границах лежит
. В каких границах лежит  ?
?
5. Пусть векторы  и
и 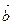 единичные. Найдите:
единичные. Найдите:
а)  , если
, если  ; б)
; б) 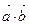 , если
, если  .
.
6. Сформулируйте свойства векторного произведения двух векторов.
7. Что вы можете сказать о векторах  и
и 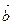 , если: а)
, если: а)  ; б)
; б)  ?
?
8. Как найти векторное произведение двух векторов в координатах?
9. Найдите координаты вектора  , если
, если 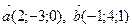 .
.
10. В чем разница между векторным и скалярным произведениями двух векторов? В чем их сходство?
11. В чем заключается геометрический смысл модуля векторного произведения двух векторов?
12. Найдите площадь параллелограмма ABCD, если 
13. Дайте определение смешанного произведения трех векторов.
14. Сформулируйте алгебраические свойства смешанного произведения трех векторов.
15. Чему равно смешанное произведение векторов  ?
?
16. Запишите формулу для нахождения смешанного произведения трех векторов, заданных своими координатами.
17. Вычислите  , если
, если 
18. В чем заключается геометрический смысл абсолютной величины смешанного произведения трех векторов?
19. Вычислите объем параллелепипеда ABCDA1B1C1D1, если 
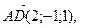
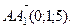
20. Установите, компланарны ли векторы  ,
, 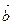 и
и 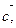 если
если  .
.
II. Типовые задачи с решениями
Задача 1. Вершины треугольника находятся в точках  Вычислите его площадь и длину высоты, проведенной из вершины В.
Вычислите его площадь и длину высоты, проведенной из вершины В.
 Решение. Воспользуемся формулой
Решение. Воспользуемся формулой 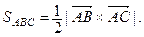
Найдем координаты векторов 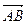 и
и 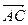 :
: 
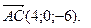
Сначала найдем координаты вектора 

 т. е.
т. е. 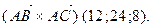
Затем найдем длину вектора 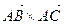 :
:
|
|
|
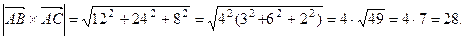
Тогда  (кв. ед. ).
(кв. ед. ).
Чтобы найти высоту ВН (рис. 22), воспользуемся формулой 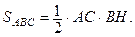
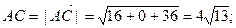 тогда
тогда 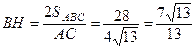 (ед. ).
(ед. ).
Ответ: 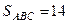 кв. ед.,
кв. ед.,  ед.
ед.
Задача 2. Найдите объем и длину высоты параллелепипеда ABCDA1B1C1D1 (рис. 23), если 

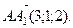
Решение.  ;
;


 Тогда
Тогда  (куб. ед. ).
(куб. ед. ).
Для нахождения высоты А1Н (рис. 23) воспользуемся формулой:  откуда
откуда 

 ;
; 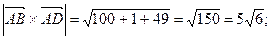
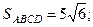

Ответ: 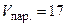 куб. ед.,
куб. ед., 
Задача 3. Докажите, что векторы  компланарны.
компланарны.
Решение. Векторы  компланарны тогда и только тогда, когда их смешанное произведение равно 0.
компланарны тогда и только тогда, когда их смешанное произведение равно 0.
 следовательно, векторы компланарны.
следовательно, векторы компланарны.
Задача 4. При каком значении x вектор  перпендикулярен вектору
перпендикулярен вектору 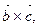 если
если 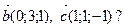
Решение. Первый способ. Найдем сначала координаты вектора 
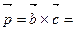
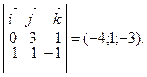 Вектор
Вектор  перпендикулярен вектору
перпендикулярен вектору  тогда и только тогда, когда
тогда и только тогда, когда 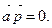 Найдем скалярное произведение
Найдем скалярное произведение 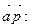
 Следовательно, получаем уравнение
Следовательно, получаем уравнение  откуда находим
откуда находим 
Второй способ. Не находя координат вектора 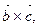 запишем условие перпендикулярности векторов
запишем условие перпендикулярности векторов  и
и 
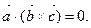 Но в левой части этого равенства стоит смешанное произведение трех векторов
Но в левой части этого равенства стоит смешанное произведение трех векторов  следовательно,
следовательно,  Подставляя в это равенство координаты векторов
Подставляя в это равенство координаты векторов  получим уравнение:
получим уравнение:
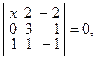 откуда
откуда  т. е.
т. е. 

Ответ: 
|
|
|


