 |
III. Задачи для упражнений. IV. Задачи для самостоятельного решения. V. Задание на дом. Занятие 8. Тема: «Аффинная и прямоугольная декартовы системы координат»
|
|
|
|
III. Задачи для упражнений
1. При каком значении m векторы 
и 
перпендикулярны?
2. Вычислите косинус угла между векторами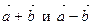 
, если 
3. Вычислите длину диагоналей параллелограмма ABCD, если 
где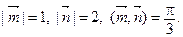 
4. Известно, что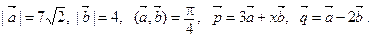 
При каком значении x векторы 
перпендикулярны?
5. Найдите вектор 
, если 
где 
6. Выясните, каким является треугольник АВС (остроугольным, прямоугольным или тупоугольным), если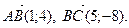 
7. В четырехугольнике ABCD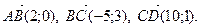 
Выясните, будут ли диагонали АС и BD взаимно перпендикулярны.
IV. Задачи для самостоятельного решения
1. Найдите числовое значение скаляра 
если:
а) 
б)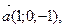 
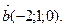
2. Найдите вектор , зная, что он перпендикулярен вектору 
где 
3. Вектор 
перпендикулярен вектору 
и вектор 
перпендикулярен вектору 
. Найдите угол между векторами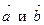 
.
4. Докажите векторным методом, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
5. Докажите векторным методом, что диагонали ромба взаимно перпендикулярны.
V. Задание на дом
1. Даны векторы 
и 
При каком значении n эти векторы перпендикулярны?
2. Вычислите скалярное произведение векторов 
и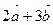 
, если 
и угол между векторами 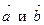равен 1200.
3. Найдите длину вектора 
если:
а) 
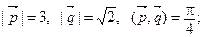б) 
4. Найдите вектор , коллинеарный вектору 
если 
где 
5. Векторы 
и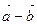 
перпендикулярны. Докажите, что 
.
Занятие 8
Тема: «Аффинная и прямоугольная декартовы системы координат»
Литература для самостоятельного изучения темы: [1], гл. III, IV; [3], гл. 1; [4], гл. 1, 2; [5], гл. I; [6], гл. I; [7], гл. 3, 4; [8], гл. 3; [9], гл. 3; [10], гл. 3, 10.
I. Контрольные вопросы и задания
1. Дайте определения следующих понятий:
а) аффинная система координат на плоскости и в пространстве;
|
|
|
б) прямоугольная декартова система координат на плоскости и в пространстве;
в) координаты точки в данной системе координат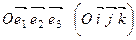 
.
2. Постройте точку 
заданную в прямоугольной декартовой системе координат 
.
3. Постройте точку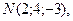 
заданную в прямоугольной декартовой системе координат 
.
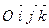4. Дана точка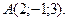 
Каковы координаты точки, ближайшей к ней и лежащей:
а) на каждой из координатных плоскостей;
б) на каждой из осей координат?
5. Найдите координаты вектора 
если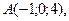 
6. В какой системе координат можно пользоваться формулой нахождения координат вектора заданного двумя точками А и В:
а) только в аффинной;
б) только в прямоугольной декартовой;
в) и в аффинной, и в прямоугольной декартовой?
7. Вектор 
имеет начало в точке 
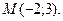Найдите координаты его конца.
8. Дайте определение деления отрезка в данном отношении.
9. Напишите формулы деления отрезка в данном отношении в координатах.
10. Найдите координаты точки С, делящей направленный отрезок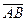 
в отношении 
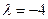, если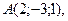 
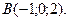
11. Найдите координаты середины отрезка с концами 
и 
12. Даны один конец отрезка (1; 1) и его середина (2; 2). Найдите второй конец отрезка.
13. В какой системе координат можно пользоваться формулами деления отрезка в данном отношении?
14. Запишите формулу для нахождения расстояния между двумя точками, заданными своими координатами.
15. Даны точки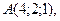 
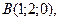
Найдите расстояние между этими точками, взятыми попарно.
16. В какой системе координат можно пользоваться формулой расстояния между двумя точками?
17. Даны точки 
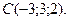Какая из них ближе всего к началу координат? К каждой из координатных плоскостей? К каждой из координатных осей?
II. Типовые задачи с решениями
Задача 1. Точки C и D лежат между точками А и В так, что AC = CD = DB. Найдите, в каком отношении:
а) точка С делит направленный отрезок ;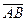
б) точка А делит направленный отрезок 
.
|
|
|
Решение. а) Пусть точка С делит направленный отрезок 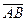в отношении l, т. е. 
. Тогда по определению деления отрезка в данном отношении
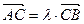. (1)
По чертежу (рис. 16) находим:
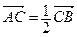. (2)
 |
Сравнивая правые части равенств (1) и (2), получаем:
.
Ответ: 
.
б) Пусть точка А делит направленный отрезок в отношении m, т. е. 
. Тогда по определению деления отрезка в данном отношении:
. (3)
По чертежу (рис. 16) находим:
. (4)
Сравнивая правые части равенств (3) и (4), получаем: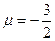 
.
Ответ: 
.
Задача 2. Постройте точки, делящие данный направленный отрезок 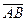(рис. 17) в отношении:
а)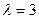 
; б) 
; в)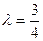 
.
Решение. а) Пусть точка С делит направленный отрезок 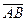в отношении 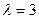. Тогда 
.
Так как l> 0, то 
, следовательно, точка С лежит внутри отрезка АВ.
Так как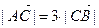 
, то отрезок АВ надо разделить на четыре равные части, и третья точка деления будет искомой точкой С (рис. 18).
 |
По чертежу (рис. 18) делаем проверку векторного равенства
.
б) Пусть точка D делит 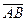в отношении . Тогда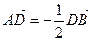 
.
l< 0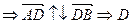 
не лежит внутри отрезка АВ.
Так как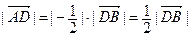 
, то точка D такова, что А лежит между D и В, причем А – середина DB (рис. 19).
 |
По чертежу (рис. 19) проверяем, что
.
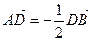в) Пусть точка Е делит 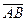в отношении 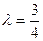. Тогда 
.
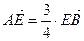l> 0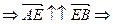 
точка Е лежит внутри отрезка АВ.
Так как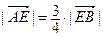 
, то отрезок АВ надо разделить на 7 равных частей, и третья точка деления будет искомой точкой Е (рис. 20).
 |
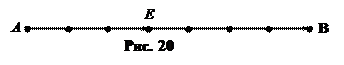По чертежу (рис. 20) проверяем справедливость векторного равенства
.
Ответ: точки C, D и E – искомые (рис. 18, 19, 20).
Задача 3. Найдите координаты точки пересечения медиан треугольника с вершинами в точках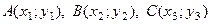 
.
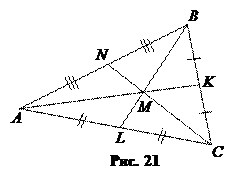Решение. Пусть 
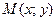– точка пересечения медиан AK, BL, CN треугольника АВС (рис. 21). Так как L – середина отрезка АС, то она имеет координаты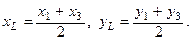 
Так как 
, то точка М делит направленный отрезок 
в отношении 
. Тогда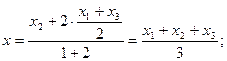 
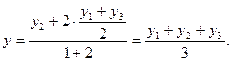
Итак, если известны координаты вершин треугольника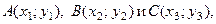 
то координаты точки пересечения его медиан определяются по формулам:
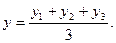Ответ: 
.
Задача 4. Докажите, что треугольник с вершинами 
прямоугольный.
|
|
|
Решение. Первый способ. Найдем координаты векторов 
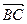и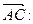 
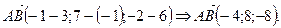Аналогично находим, что 
.
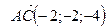Выясним, будут ли векторы 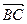и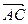 
попарно взаимно перпендикулярны:
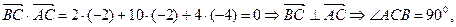т. е. 
– прямоугольный.
Второй способ. Воспользуемся теоремой, обратной теореме Пифагора. Для этого найдем квадраты длин сторон DАВС:
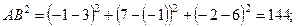
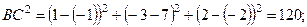
Тогда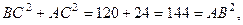 
следовательно, DАВС – прямоугольный ( 
).
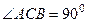Задача 5. На оси Оy найдите точку, равноудаленную от точек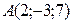 
и 
.
Решение. Пусть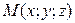 
– искомая точка. Так как 
, то ее абсцисса и аппликата равны нулю, т. е. x = 0 и z = 0. Следовательно, 
.
Так как М равноудалена от точек А и В, то АМ = ВМ, откуда получаем уравнение: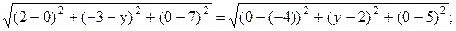 
После возведения в квадрат и упрощения получаем: 
т. е. 
.
Ответ: .
|
|
|
