 |
III. Задачи для упражнений. IV. Задачи для самостоятельного решения. V. Задание на дом. Занятие 7. Тема: «Скалярное произведение векторов»
|
|
|
|
III. Задачи для упражнений
1. Даны три вектора  . Найдите координаты вектора
. Найдите координаты вектора  в базисе
в базисе 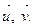
2. АА1, ВВ1, СС1 – медианы треугольника АВС, М – его центр тяжести. Найдите координаты векторов  в базисе
в базисе 
3. Р – точка пересечения диагоналей произвольного параллелепипеда 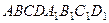 . Найдите координаты вектора
. Найдите координаты вектора 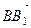 в базисе
в базисе 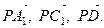
4. Среди векторов 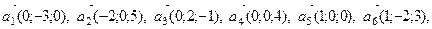
 заданных в базисе
заданных в базисе  укажите векторы, компланарные с
укажите векторы, компланарные с  . Ответ поясните.
. Ответ поясните.
5. Даны векторы 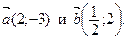 При каких значениях t будут коллинеарны векторы
При каких значениях t будут коллинеарны векторы 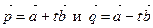 ?
?
IV. Задачи для самостоятельного решения
1. В базисе  даны векторы
даны векторы 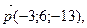


 Представьте вектор
Представьте вектор  как линейную комбинацию векторов
как линейную комбинацию векторов 
2. ABCDEF – правильный шестиугольник, О – его центр. Найдите координаты векторов  в базисе
в базисе 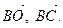
3. В равнобокой трапеции ABCD AB – нижнее основание (AB > DC), угол BAD равен 600. Найдите координаты векторов  в базисе
в базисе 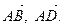
4. Дан произвольный параллелепипед 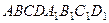 . Найдите координаты векторов
. Найдите координаты векторов 
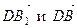 в базисе
в базисе 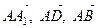 и представьте вектор
и представьте вектор 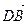 в виде линейной комбинации векторов
в виде линейной комбинации векторов 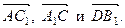
V. Задание на дом
1. Даны векторы 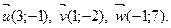 Найдите координаты вектора
Найдите координаты вектора 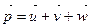 в базисе
в базисе 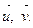
2. М – точка пересечения медиан 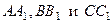 треугольника АВС. Найдите координаты вектора
треугольника АВС. Найдите координаты вектора  в базисе
в базисе 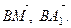
3. О – центр основания ABCD правильной четырехугольной пирамиды PABCD. Найдите координаты вектора  в базисе
в базисе 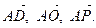
4. При каком значении m векторы  коллинеарны?
коллинеарны?
Занятие 7
Тема: «Скалярное произведение векторов»
Литература для самостоятельного изучения темы: [1], гл. IV; [2], разд. I, гл. 2; [3], гл. 2; [4], гл. 2; [5], гл. I; [6], гл. I; [7], гл. 3; [8], гл. 3; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Дайте определение угла между двумя векторами.
2. В каких пределах находится величина угла между двумя векторами: от 0 до p, от 0 до 2p или от 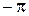 до p?
до p?
|
|
|
3. Дайте определение скалярного произведения двух векторов.
4. Дайте определение скалярного квадрата вектора.
5. Каков знак скалярного произведения двух векторов, если угол между ними:
а) острый; б) тупой?
6. Сформулируйте свойства скалярного произведения векторов.
7. Векторы 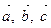 единичные,
единичные, 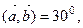
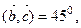
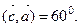 Вычислите:
Вычислите:
а) 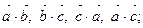 б)
б) 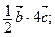 в)
в) 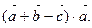
8. Сформулируйте необходимое и достаточное условие перпендикулярности (ортогональности) двух векторов.
9. Чему равно скалярное произведение двух векторов, заданных координатами?
10. Найдите скалярное произведение векторов 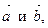 если:
если:
а) 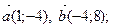 б)
б) 
11. Выясните, перпендикулярны ли векторы:
а)  б)
б) 
12. Чему равна длина вектора, заданного координатами?
13. Найдите длину вектора  если:
если:
а)  б)
б) 
14. Напишите формулу для вычисления косинуса угла между двумя векторами.
15. Вычислите угол между векторами 
16. Докажите, что векторы 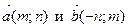 либо перпендикулярны, либо равны нулевому.
либо перпендикулярны, либо равны нулевому.
17. Возможно ли для трех ненулевых векторов соотношение 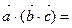


II. Типовые задачи с решениями
Задача 1. Вычислите  где
где 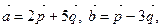 если:
если:
а) 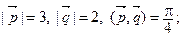 б)
б) 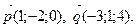
Решение. а) Воспользуемся свойствами и определением скалярного произведения векторов:


б) Найдем координаты векторов  и
и 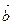 :
: 

Затем воспользуемся формулой для нахождения скалярного произведения векторов в координатах: 
Ответ: а) 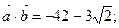 б)
б) 
Задача 2. Найдите координаты единичного вектора, ортогонального вектору  и вектору
и вектору 
Решение. Пусть  искомый вектор. По условию задачи имеем:
искомый вектор. По условию задачи имеем: 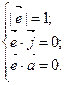
Учитывая, что  получили систему трех уравнений с тремя неизвестными:
получили систему трех уравнений с тремя неизвестными:

 Решая систему, получим:
Решая систему, получим: 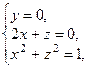
 откуда
откуда 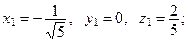

Таким образом, существует два вектора 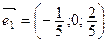 и
и 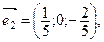 удовлетворяющих условию задачи (они являются противоположными) (рис. 13).
удовлетворяющих условию задачи (они являются противоположными) (рис. 13).
Ответ: 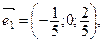

Задача 3. Найдите вектор  , коллинеарный вектору
, коллинеарный вектору  если
если 
Решение. Так как векторы  и
и  коллинеарны, то их координаты пропорциональны, поэтому можно записать:
коллинеарны, то их координаты пропорциональны, поэтому можно записать:  где t – некоторое действительное число. Найдем t.
где t – некоторое действительное число. Найдем t.
|
|
|
Так как 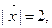 то
то 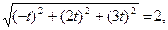 т. е.
т. е. 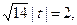 откуда
откуда 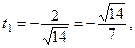
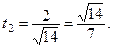 Тогда
Тогда 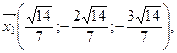
 т. е. задача имеет два решения.
т. е. задача имеет два решения.
Эти векторы являются противоположными (рис. 14).
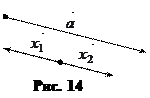 Ответ:
Ответ: 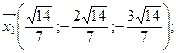
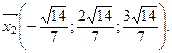
Задача 4. Найдите длину диагонали АС ромба ABCD, у которого длины сторон равны 1 и угол BAD равен 300.
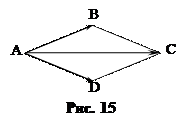 Решение. По правилу параллелограмма
Решение. По правилу параллелограмма 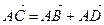 (рис. 15).
(рис. 15).
Найдем  :
:
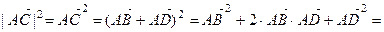

 откуда находим
откуда находим 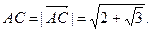
Ответ: 
Задача 5. Длины ненулевых векторов  и
и 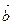 равны. Найдите угол между этими векторами, если известно, что векторы
равны. Найдите угол между этими векторами, если известно, что векторы  перпендикулярны.
перпендикулярны.
Решение. Так как  , то
, то 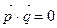 , т. е.
, т. е.  .
.
Воспользуемся свойствами скалярного произведения: 

По определению скалярного произведения 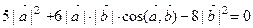 , откуда при
, откуда при 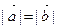 получаем:
получаем: 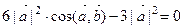 ,
, 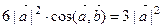 .
.
Поскольку  , то находим
, то находим  .
.
Следовательно, угол между векторами 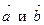 равен
равен  .
.
Ответ:  .
.
|
|
|


