 |
III. Задачи для упражнений. IV. Задачи для самостоятельного решения. V. Задание на дом. Занятие 3. Тема: «Ранг матрицы». I. Контрольные вопросы и задания
|
|
|
|
III. Задачи для упражнений
1. Вычислите определители второго порядка:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
2. Вычислите определители третьего порядка:
а) 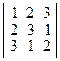 ; б)
; б)  ; в)
; в) 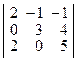 .
.
3. Как изменится определитель, если ко всем его строкам, начиная со второй, прибавить первую строку?
4. Как изменится определитель, если все его столбцы написать в обратном порядке?
5. Путем разложения по элементам четвертой строки вычислите определитель 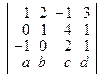 .
.
6. Вычислите коэффициент при х в разложении определителя 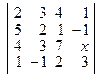 .
.
7. Вычислите определители:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
8. Найдите матрицы, обратные данным:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 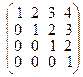 .
.
IV. Задачи для самостоятельного решения
1. Вычислите определители:
а)  ; б)
; б)  ;
;
в) 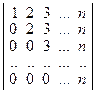 ; г)
; г) 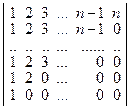 .
.
2. Пользуясь определением определителя, вычислите коэффициенты при  и
и 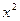 в выражении f(x) =
в выражении f(x) =  .
.
3. Числа 104, 143, 231 делятся на 13. Докажите, что делится на 13 определитель 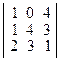 , не вычисляя этого определителя.
, не вычисляя этого определителя.
4. Найдите матрицы, обратные данным:
а)  ; б)
; б)  ; в)
; в)  .
.
V. Задание на дом
1. Разложите по элементам третьего столбца и вычислите определитель:
 .
.
2. Вычислите определители:
а)  ; б)
; б) 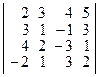 ; в)
; в) 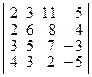 ;
;
г)  ; д)
; д) 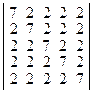 .
.
3. Найдите матрицы, обратные данным:
а)  ; б)
; б)  ; в)
; в) 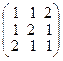 ; г)
; г)  .
.
Занятие 3
Тема: «Ранг матрицы»
Литература для самостоятельного изучения темы: [5], гл. 5; [6], гл. VI; [7], гл. 1; [8], гл. 2.
I. Контрольные вопросы и задания
1. Что называют минором k-го порядка матрицы Аmxn?
2. Найдите миноры второго и третьего порядков матрицы  .
.
3. Дайте определение ранга матрицы.
4. Каким числом может выражаться ранг матрицы Аmxn?
5. В каком случае ранг матрицы равен нулю?
6. В каком случае квадратная матрица k-го порядка имеет rang=k?
7. Перечислите свойства ранга матрицы.
8. При помощи каких преобразований ранг матрицы не меняется?
|
|
|
9. На чем основан метод окаймляющих миноров?
10. Найдите ранг матрицы: 
11. Дайте формулировку теоремы Кронекера-Капелли.
12. Что называют базисным минором матрицы?
II. Типовые задачи с решениями
Задача 1. Найдите ранг матрицы А с помощью элементарных преобразований, если 
Решение. Применив элементарные преобразования, приводим данную матрицу к треугольному виду: 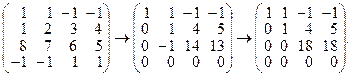
Вторая матрица получена из первой путем поочередного умножения первой строки на (–1), (–8), 1 и прибавления ко второй, третьей и четвертой строкам; третья получена из второй путем прибавления второй строки к третьей.
Ранг последней матрицы равен трем, так как имеется отличный от нуля минор третьего порядка этой матрицы.  , а определитель самой матрицы (определитель четвертого порядка) равен нулю. Следовательно, ранг исходной матрицы равен трем.
, а определитель самой матрицы (определитель четвертого порядка) равен нулю. Следовательно, ранг исходной матрицы равен трем.
Ответ: rangA = 3.
Задача 2. Вычислите методом окаймляющих миноров ранг матрицы 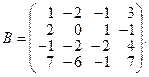
Решение. Очевидно, что матрица В имеет ненулевые миноры первого и, по крайней мере, второго порядка: 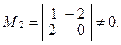
Максимальный порядок минора матрицы В равен 4. Следовательно, 
Составим и вычислим последовательно миноры третьего порядка, окаймляющие найденный минор второго порядка.



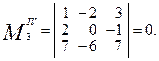
Все миноры третьего порядка, окаймляющие минор второго порядка, равны нулю, значит, ранг матрицы В равен 2.
Ответ: rangB = 2.
Задача 3. Определите с помощью теоремы Кронекера-Капелли совместность систем и решите их:
а)  б)
б) 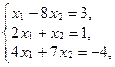
Решение.
а) Основная расширенная матрица данной системы имеет вид: 
Найдем ранг этой системы, приводя ее матрицу к ступенчатому виду: 
Ранг основной матрицы совпадает с рангом расширенной матрицы и равен 2, значит, система совместна, но так как ранг основной матрицы меньше числа неизвестных (n = 3), то множество ее решений является бесконечным.
В матрице минор 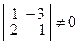 , ему соответствует система уравнений
, ему соответствует система уравнений  , в которой
, в которой 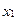 и
и  – базисные неизвестные,
– базисные неизвестные, 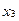 – свободная неизвестная. Выразим
– свободная неизвестная. Выразим 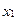 и
и  через
через 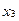 , получим:
, получим: 
|
|
|
Ответ:  , где
, где 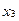 – любое действительное число.
– любое действительное число.
б) Основная расширенная матрица данной системы имеет вид: 
Найдем ранг этой системы: 
Ранг основной матрицы равен двум, а ранг расширенной – трем, следовательно, система несовместна.
Ответ: система несовместна.
|
|
|


