 |
III. Задачи для упражнений. IV. Задачи для самостоятельного решения. V. Задание на дом. Занятие 10. Тема: «Различные уравнения прямой на плоскости.
|
|
|
|
III. Задачи для упражнений
1. Вычислите синус угла, образованного векторами  и
и 
2. Вычислите площадь треугольника, вершины которого находятся в точках 

3. Найдите длину высоты ВН параллелограмма ABCD, проведенной к основанию AD, если 

4. Вычислите объем треугольной пирамиды, вершины которой находятся в точках 


5. Даны вершины тетраэдра 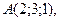

 Найдите длину его высоты, опущенной из вершины D.
Найдите длину его высоты, опущенной из вершины D.
6. Будут ли компланарны векторы:
а)  ; б)
; б)  ?
?
7. Выясните, лежат ли точки 
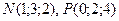 и
и 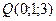 в одной плоскости.
в одной плоскости.
8. При каком значении y вектор  перпендикулярен вектору
перпендикулярен вектору 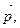 если
если 

IV. Задачи для самостоятельного решения
1. Площадь треугольника АВС равна 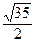 кв. ед. Две его вершины находятся в точках
кв. ед. Две его вершины находятся в точках  и
и  Найдите координаты третьей вершины С, если она лежит на оси Oz.
Найдите координаты третьей вершины С, если она лежит на оси Oz.
2. Вектор  перпендикулярен к векторам
перпендикулярен к векторам 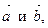 угол между
угол между 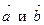 равен 300. Зная, что
равен 300. Зная, что 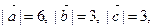 вычислите
вычислите 
3. Дан параллелепипед ABCDA1B1C1D1, построенный на векторах 
 и
и 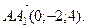 Найдите: а) косинус угла между гранями
Найдите: а) косинус угла между гранями 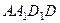 и
и 
б) объем параллелепипеда;
в) площади граней;
г) длину высоты, проведенной из вершины А1 на грань 
4. Объем тетраэдра V = 5, три его вершины находятся в точках 

 Найдите координаты четвертой вершины D, если известно, что она лежит на оси Oy.
Найдите координаты четвертой вершины D, если известно, что она лежит на оси Oy.
V. Задание на дом
1. Даны точки 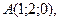
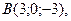
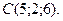 Вычислите площадь треугольника АВС.
Вычислите площадь треугольника АВС.
2. Даны вершины треугольника 
 и
и 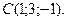 Вычислите длину его высоты, опущенной из вершины В на сторону АС.
Вычислите длину его высоты, опущенной из вершины В на сторону АС.
3. В треугольной призме 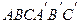
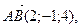
 и
и 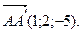 Вычислите: а) объем призмы;
Вычислите: а) объем призмы;
б) площади граней;
в) длину высоты призмы.
4. Объем треугольной пирамиды равен 9. Три его вершины находятся в точках 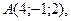

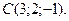 Найдите координаты четвертой вершины D, если она находится на оси Oz.
Найдите координаты четвертой вершины D, если она находится на оси Oz.
Занятие 10
Тема: «Различные уравнения прямой на плоскости.
|
|
|
Взаимное расположение двух прямых на плоскости»
Литература для самостоятельного изучения темы: [1], гл. V; [2], разд. I, гл. 1; [3], гл. 1; [4], гл. 1; [5], гл. II; [6], гл. II; [7], гл. 5; [8], гл. 5; [9], гл. 3; [10], гл. 3.
I. Контрольные вопросы и задания
1. Напишите следующие уравнения прямой:
а) каноническое; б) векторное; в) параметрические.
2. Составьте каноническое и параметрические уравнения прямой, заданной точкой 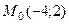 и направляющим вектором
и направляющим вектором 
3. Напишите параметрические уравнения прямой 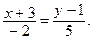
4. Напишите каноническое уравнение каждой из данных прямых:
а) 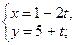 ; б)
; б)  ; в)
; в) 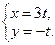
5. Напишите уравнение прямой, проходящей через две точки 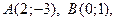 и найдите координаты направляющего вектора этой прямой.
и найдите координаты направляющего вектора этой прямой.
6. Постройте прямую:
а)  б)
б) 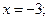 в)
в)  г)
г) 
7. Напишите общее уравнение прямой. Каков смысл коэффициентов А и В в общем уравнении этой прямой, заданной в аффинной системе координат?
8. Найдите координаты направляющего вектора каждой из данных прямых:
а) 7x + 2y – 1 = 0; б) 3x – 4 = 0; в) y + 5 = 0; г) x + 10 = 0.
9. Составьте уравнение прямой, проходящей через точку  параллельно прямой:
параллельно прямой:
а)  б)
б) 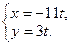
10. Запишите уравнение прямой с угловым коэффициентом. Каков геометрический смысл коэффициентов этого уравнения?
11. Составьте уравнение прямой с угловым коэффициентом, проходящей через точку 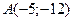 если
если 
12. Напишите уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом.
13. Найдите уравнение прямой, проходящей через точку 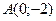 и имеющей угловой коэффициент
и имеющей угловой коэффициент 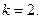
14. Найдите коэффициенты k и b прямой 
15. Составьте уравнение прямой, проходящей через начало координат и составляющей с положительным направлением оси Ox углы: а)  б)
б) 
16. Под каким углом к положительному направлению оси Ох наклонены прямые 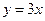 и
и 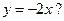
17. Найдите угловой коэффициент прямой, проходящей через точки 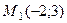 и
и 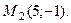
18. Найдите координаты точек пересечения прямой 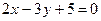 с осями координат.
с осями координат.
|
|
|
19. Каковы условия пересечения, параллельности и совпадения прямых?
20. Укажите взаимное расположение следующих пар прямых (в случае пересечения найдите их общую точку):
а)  и
и  б)
б) 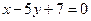 и
и 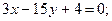
в)  и
и  г)
г) 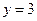 и
и 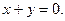
|
|
|


