 |
Принцип управления по возмущению (принцип компенсации)
|
|
|
|
Принцип управления по отклонению (принцип обратной связи).
Если в автоматической системе управляющее воздействие x(t) вырабатывается на основе информации об отклонении управляемой величины u(t) от требуемого значения, то система построена на основе принципа управления по отклонению, или принципа обратной связи. Для реализации этого принципа в УУ необходимо осуществлять давление действительного значения управляемой величины с требуемым (предписанным) значением и управлять ОУ в зависимости от результатов этого сравнения.
Принцип управления по возмущению (принцип компенсации)
Если управляющее воздействие в САУ x(t) вырабатывается в зависимости от результатов измерения возмущения, действующего на объект, то такая система построена на принципе компенсации. Системы, построенные по этому принципу, работают по разомкнутой цепи, т. е. не имеют обратной связи.
Принцип разомкнутого управления:
САУ с разомкнутой цепью воздействий называется система, в которых управляющее воздействие вырабатывается в функции задающего воздействия, а в общем случае - в функции общих воздействий одновременно. В системах, использующих этот принцип, управление осуществляется на основе заданного алгоритма функционирования и не контролируется выходным и возмущающими воздействиями.
Недостатком такого принципа является слабая защищенность от возмущающих воздействий.
3 Основные законы регулирования САУ.
Под законом управления понимается алгоритм или функциональная зависимость, в соответствии с которыми УУ формирует управляющее воздействие 
.
Закон пропорционального регулирования выражается функциональной зависимостью.
|
|
|
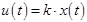где k - коэффициент усиления системы.
Пропорциональное регулирование позволяет уменьшить ошибки в объекте. Регулирование в этом случае является статическим, так как при любом конечном значении коэффициента усиления ошибка будет отлична от 0.
Закон дифференциального регулирования выражается функциональной зависимостью:
Дифференциальное регулирование используется в переходных процессах и в качестве вспомогательного средства, так как позволяет учитывать не только наличие ошибки, но и тенденцию к росту или уменьшению ошибки.
Закон интегрального регулирования выражается функциональной зависимостью:
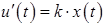
Таким образом, законы регулирования (управления) позволяют выбрать алгоритм или функциональную зависимость, в соответствии с которыми УУ формирует управляющее воздействие
4 Составление дифференциальных уравнений элементов автоматической системы.
В основе построения САУ лежит одна главная задача – преобразовать входное воздействие 
в выходную величину 
(рис.1): 
, где 
- оператор преобразования воздействий.
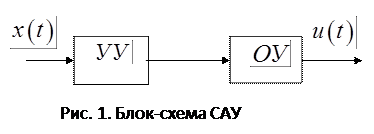Для составления д.у. САУ требуется на основе её принципа действия разработать структурно-функциональную схему в виде взаимосвязанных элементов, каждый из которых выполняет свою функцию (рис. 1). Для каждого элемента системы составляется д.у., связывающее выходную величину с входной.
Уравнения, связывающие входное, выходное и возмущающие воздействия, а также их производные называются уравнениями динамики, которые имеют следующий вид:
(1); где 
- функциональная зависимость; 
- выходное воздействие и его производные;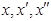 
- входное воздействие и его производные; 
- возмущающее воздействие.
Уравнение динамики описывает поведение системы в неустановившемся (переходном режиме).
Если входное воздействие станет постоянным (установившимся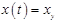 
) и система перейдет в установившийся режим 
), то такое состояние САУ описывается уравнением статики. Уравнение статики связывает входное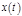 
и выходное воздействие 
при их установившемся состоянии и имеет следующий вид:
|
|
|
(2); где 
- функциональная зависимость;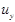 
- выходное установившееся воздействие; 
- входное установившееся воздействие; 
- возмущающее воздействие.
Для описания САУ каждый ее элемент описывается д.у. динамики. Количество д.у.должно равняться числу зависимых (регулируемых) переменных. Исключаются промежуточные переменные из-за связи между элементами системы: выходная величина одного элемента является входной величиной для другого элемента. Получают одно д.у., в котором независимыми переменными являются внешние воздействия и время, а зависимыми переменными являются управляемые величины или ошибка системы.
5 Операторный метод решения линейных дифференциальных уравнений. Преобразования Лапласа.
Сущность операторного метода заключается в том, что посредством интегрального преобразования осуществляется переход от д.у. к вспомогательному алгебраическому уравнению, которое решается обычными способами. Решения алгебраического уравнения путем обратного преобразования превращают в исходное д.у.
В качестве интегрального преобразования часто используют преобразование Лапласа. Прямое интегральное преобразование Лапласа выражается следующим выражением:
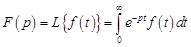
где 
– изображение функции 
; 
– оригинал (исходная, заданная функция); 
– символический оператор дифференцирования (комплексная переменная вида 
; 
– вещественная часть; 
– множитель при мнимой единице 
).
Формы записи: 
Обратный переход из изображений к оригиналу осуществляется на основе обратного преобразования Лапласа:
Символика обозначений 
.
|
|
|
