 |
Основные теоремы (свойства) преобразования Лапласа
|
|
|
|
1. Свойство линейности, т.е. 
где 
в общем случае комплексные константы.
2. Теорема подобия.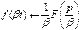 
. При умножении аргумента оригинала на положительный множитель аргумент соответствующего изображения и само изображение делится на этот множитель.
3. Теорема смещения. 
, где 
– комплексная константа.
4. Теорема об изображении производной оригинала.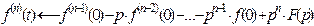 
при условии, что существуют производные оригинала до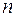 
-го порядка включительно.
5. Теорема запаздывания. 
, где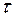 
– положительная константа.
Замечание: 
.
6. Теорема свертывания (свертки). Пусть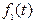 
и 
– оригиналы, тогда справедливо следующее выражение 
= 
,
где 
.
Замечание. Интеграл в средней части называется сверткой двух оригиналов и обозначается 
.
Свойства сверток:
а) если 
и 
– оригиналы, то 
тоже оригиналы по Лапласу;
б) Свертка не зависит от порядка сомножителей 
.
На основе определения преобразования Лапласа и приведенных теорем можно получить изображения для часто встречающихся оригиналов.
6 Передаточные функции САУ в операторной форме.
Облегчение расчетов наступает с использованием передаточных функций (ПФ). ПФ характеризуют динамические и статические свойства САУ.
ПФ – это отношение операторного изображения выходной величины 
к операторному изображению входной величины 
при нулевых начальных условиях.
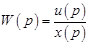, при 
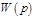является математической основой, так называемого метода передаточных функций: зная передаточную функцию, можно найти решение дифференциального уравнения с нулевыми начальными условиями по изображению.
ПФ разомкнутой системы очень часто используют в ОТУ. Если в структурной схеме САУ элементы включены последовательно, то ПФ разомкнутой САУ равна произведению передаточных функций последовательно включенных элементов. По передаточной функции САУ можно определить статические качества системы. Для оценки динамических качеств требуются дополнительные исследования самой системы.
|
|
|
Рассмотрим ПФ с позиций линейных д.у. (л.д.у.). Пусть дана САУ, которая описывается (л.д.у.) с постоянными коэффициентами:
Условно будем считать, что оператор дифференцирования 
является алгебраической величиной (алгебраический сомножитель), а выражение 
- произведение, не обладающее свойством коммутативности. Произведем замену и получим:
Введем обозначения: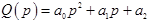 
- называется собственным оператором САУ (или ее элемента); 
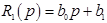- называется оператором по управляющему воздействию; 
- называется оператором по возмущающему воздействию.
Перепишем уравнение (*) с учетом введенных обозначений: 
Отношение оператора воздействия к собственному оператору системы называют передаточной функцией в операторной (символической) форме.
Передаточная функция по управляющему воздействию 
имеет вид: 
.
Передаточная функция по возмущающему воздействию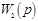 
имеет вид: 
.
Используя передаточные функции можно записать: 
Таким образом, понятие ПФ весьма удобно при анализе так называемых структурных схем. ПФ звеньев или отдельных участков схемы позволяют легко получить общее уравнение всей системы, а в дальнейшем, при необходимости, перейти к исходному д.у.
7 Передаточные функции САУ в форме изображения Лапласа.
Более строго ПФ определяется через изображения Лапласа или Карсона–Хевисайда.
Применим преобразование Лапласа к правой и левой частям исходного д.у.
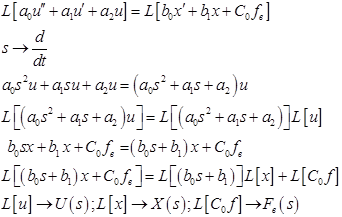
где 
– изображение выходного воздействия;
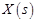– изображение входного воздействия;
– изображение возмущающего воздействия.
Передаточной функцией в форме изображения Лапласа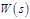 
называется отношение изображения выходного воздействия к изображению входного воздействия при нулевых начальных условиях. Если система или ее элемент имеет несколько входов, то при определении передаточной функции относительно одного из входных воздействий остальные входные величины полагают равными нулю. Так:
|
|
|
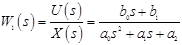- передаточная функция по управляющему воздействию;
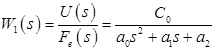- передаточная функция по возмущающему воздействию.
8 Частотные характеристики САУ
В теории автоматического управления для оценки динамики САУ широко используют амплитудно-фазовые частотные характеристики (АФЧХ), которые еще называют комплексными передаточными функциями или комплексными коэффициентами усиления.
(АФЧХ) – это отношение выходной величины САУ ко входной при условии, что входная величина изменяется по гармоническому закону с различными частотами в интервале 
, т.е. 
, где 
- амплитуда входного воздействия; 
- частота входного воздействия; 
- фаза входного воздействия.
Для линейных систем справедлив принцип суперпозиции, который заключается в следующем: реакция САУ на несколько одновременно действующих воздействий равна сумме реакций на каждое отдельное воздействие. Принцип суперпозиции позволяет рассматривать САУ с одним входом. Для САУ, описываемой линейным д.у. второго порядка 
имеем
ПФ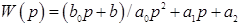 
.
Частотной передаточной функцией системы называют функцию 
, которая получается из ПФ 
путем замены оператора дифференцирования 
на комплексный аргумент 
:
АФЧХ – комплексная величина, поэтому для замкнутой системы её можно представить в виде:
где 
- действительная часть передаточной функции;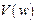 
- мнимая часть передаточной функции;
- амлитудно - частотная функция, может быть определена по формуле:
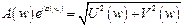
- фазовая частотная функция САУ, может быть определена по формуле:
Графики амплитудной частотной (АЧФ) и фазовой частотной функций (ФЧФ) называют амплитудной частотной (АЧХ) и фазовой частотной характеристиками (ФЧХ).
При гармоническом воздействии на систему выходное воздействие после окончания переходного процесса будет также подчиняться гармоническому закону. Амплитуда и фаза выходного воздействия будет отличаться от амплитуды и фазы входного воздействия. Рассмотрим эти отличия.
Отношение амплитуд выходного и входного воздействий равно амплитудной функции:
|
|
|
,
где 
- амплитуда (модуль) выходного воздействия; 
- амплитуда (модуль) входного воздействия.
Разность фаз выходного и входного воздействий равно фазовой функции системы:
где 
– фаза выходного воздействия;
– фаза входного воздействия.
9 Весовые функции САУ.
Весовой w2(t) называется функция, описывающая реакцию САУ на единичное импульсное воздействие, поданное на его вход.
Единичный импульс можно представить, как узкую полосу с единичной площадью. Единичный импульс (функция) описывается дельта – функцией δ(t), свойства которой мы и рассмотрим (рис. 2).
 |
1. Функция имеет площадь, равную единице, т.е.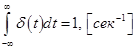 
;
2. 
;
3. 
;
4. 
.
Функция веса (ФВ) САУ связана с ее ПФ преобразованием Лапласа: ПФ есть отображение ФВ и связана с ней интегральным преобразованием:
Доказательство: исходное д.у.
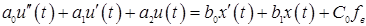перепишем в форме изображения Лапласа:
Если на вход системы (элемента системы) подать единичное импульсное воздействие, то с ее выхода можно снять сигнал, описываемый весовой функцией, т.е. если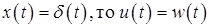 
;
Таким образом, весовая функция – обратное преобразование Лапласа от ПФ.
10 Переходные функции систем автоматического управления.
Переходной 
называется функция, описывающая реакцию САУ на единичное ступенчатое воздействие, поданное на её вход.
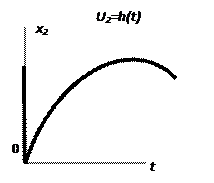Входное воздействие называется единичной ступенчатой функцией 
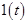, свойства которой мы и рассмотрим.
 |
1. 
Предполагается, что единица имеет ту же размерность, что и физическая величина на входе САУ.
2. 
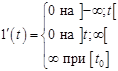
Если входное воздействие представляет собой не единичную ступенчатую функцию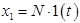 
то выходная величина будет равна 
.
Переходная функция 
- это отношение выходной величины САУ 
к высоте ступенчатого скачка 
на выходе системы, т.е. 
.
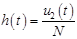Размерность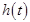 
соответствует размерности ПФ САУ.
Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот валика следящей САУ.
|
|
|
Умножение какой-либо функции времени 
на единичную ступенчатую функцию 
означает, что функция времени 
будет существовать только при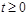 
, а при 
она обращается в нуль.
Переходная функция свяана с ПФ преобразованием Карсона, т.е. имеет место интегральное преобразование
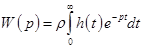
Нетрудно установить связь между функциями переходной и весовой. Если на вход САУ подать единичное ступенчатое воздействие, то с ее выхода можно снять сигнал, описываемый переходной функцией, т.е. если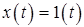 
, то 
.
По свойству преобразования Лапласа имеем: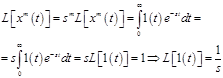 
Тогда
На основании последних уравнений получим:
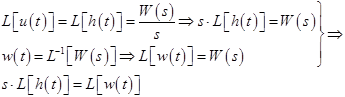
Т.к. при нулевых начальных условиях (н.н.у.) умножение изображения на s соответствует дифференцированию оригинала, то получим
Т.к. при нулевых начальных условиях умножение изображения на 
соответствует дифференцированию оригинала то получим
Отметим важные соотношения:
1. 
; 2. 
11 Правила построения структурных схем САУ.
Изучение любой САУ начинается с составления ее структурно - функциональной схемы (СФС).СФС – это графическое изображение элементов САУ и связи между ними.
СФС составляется на основе принципиальной схемы
Таким образом, СФС – «укрупненная и огрубленная» модель принципиальной схемы. СФС или блок схема простейшей динамической САУ показана на рис. 1.
 |
На примере блок-схемы (рис. 1) рассмотрим правила построения СС (рис. 2).
1. Нарисуем динамические звенья направленного действия с известными ПФ: они изображаются прямоугольниками, внутри которых записываются операторы преобразования сигналов (ПФ).
2. Связи (соединения звеньев) обозначается линиями со стрелками, указывающими направление передачи воздействий, различают прямые и обратные связи.
3. Сумматоры, в которых складываются или вычитаются воздействия, обозначаются в виде окружности, разделенной на четыре сектора. Если воздействия вычитаются, то сектор внутри окружности зачеркивается.
4. Разветвления, в которых воздействия расходятся на два или более направлений – обозначаются зачерненными точками.
По СС (рис. 2) можно получить д.у. САУ и, наоборот, по д.у. можно построить СС. Уравнения САУ могут быть представлены в различной форме: операторной или дифференциальной. Для представления уравнений в дифференциальной форме необходимо осуществить переход от 
и 
к 
и 
, а оператор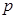 
и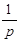 
соответственно заменить знаками производной и интегралом.
При любых видах соединений линейных звеньев, полученная в результате соединений САУ, будет линейной. Рассмотрим передаточные функции типовых соединений звеньев.
|
|
|
В образованной цепи воздействия передаются последовательно от одного звена к другому. Как найти ПФ САУ?
Для первого звена, в соответствии с определением ПФ, имеем: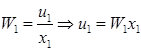 
Для второго звена: 
Для третьего звена: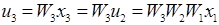 
Так как 
и 
, то можно записать
(**) 
?
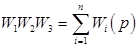Из выражения (**) следует, что ПФ САУ последовательно соединенных звеньев равна произведению ПФ всех звеньев, входящих в соединение.
Суммирующим звеном (сумматором) называется звено с одним или более входом и одним выходом, а выходное воздействие – равно сумме или разности входных воздействий.
В САУ имеет место сравнивающее звено – это звено с двумя входами и одним выходом. Выходное воздействие равно одному из входных воздействий: если 
и равно нулю в обратном случае.
Параллельным (согласным) называется такое соединение звеньев, при котором входные воздействия всех звеньев одинаковы, а их реакции алгебраически суммируются.
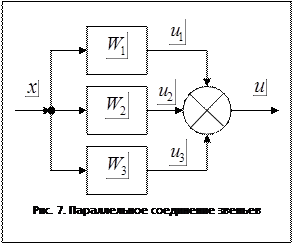Параллельное соединение звеньев показано на рис. 7. На вход системы подается воздействие 
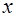; на выходе получаются воздействия равные:
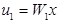
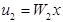
При параллельном соединении ПФ равна сумме ПФ звеньев.
Обратная связь. Понятие обратная связь имеет фундаментальное понятие в теории управления. Обратная связь может быть как положительной, так и отрицательной. Обратной связью называются цепь передачи воздействий с выхода САУ (звена) на ее вход.
Говорят, что звено охвачено обратной связью, если его выходное воздействие через какое-либо другое звено подается на его вход, где складывается с (вычитается из) входным воздействием (рис. 8).
Если входной сигнал 
складывается с сигналом обратной связи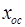 
,то обратная связь называется положительной, если из входного сигнала 
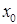вычитается сигнал обратной связи 
, то обратная связь называется отрицательной: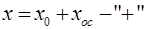 
Для САУ с положительной обратной связью (рис. 8) справедливы следующие соотношения:
1. На вход первого звена в прямой цепи подается сигнал, равный алгебраической сумме:
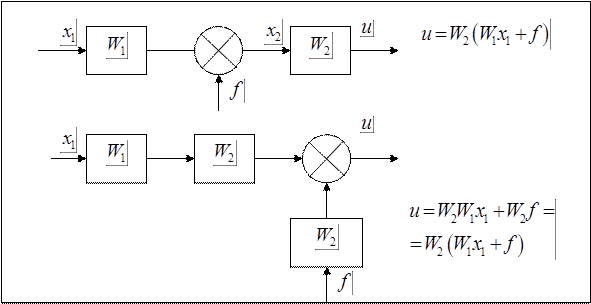
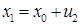или 
(1) – уравнение замыкания системы (контура);
2. 
(2) – уравнение прямой цепи;
3. 
(3) – уравнение цепи обратной связи;
4. Рассматривая совместно уравнения (1), (2) и (3) получим: 
.
5. В соответствии с общим определением искомая ПФ САУ с обратной связью 
равна отношению изображения выходного сигнала к изображению входного сигнала по Лапласу при нулевых начальных условиях.
Имеем: 
Для САУ с отрицательной обратной связью справедливы соотношения:
1. Уравнение замкнутой САУ: 
;
2. Уравнение прямой цепи 
;
3. Уравнение цепи обратной связи 
;
4. 
5. ПФ САУ с обратной связью 
равна 
Таким образом, ПФ САУ, охваченной обратной связью, равна частному, в числителе которого стоит ПФ охватываемого звена, а в знаменателе – сумма (разность) единицы и произведения ПФ охватываемого звена на ПФ звена обратной связи.
12 Правила преобразования структурных схем САУ.
При преобразовании СС наибольшее применение находят правила переноса сумматора и узлов.
При переносе сумматора по ходу сигнала (рис. 9) в СС необходимо добавить звено с ПФ, равной ПФ звена, через который переносится сумматор.
При переносе сумматора против хода сигнала (рис. 10) в структурную схему добавляется звено ПФ, обратной ПФ звена, через который переносится сумматор.
При переносе узла по ходу сигнала (рис. 11) в СС добавляется звено с ПФ обратной ПФ звена, через который переносится узел.
При переносе узла против хода сигнала (рис. 12) в СС добавляется звено с ПФ, равной ПФ звена, через которое переносится узел.
Понятие устойчивости.
Возмущенным называется движение, при котором координаты отличаются от координат при невозмущенном движении.
Устойчивым называется движение, у которого после приложения внешнего воздействия координаты точки не будут отличаться от заданных координат на заранее заданное значение величины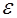 
, т.е. 
.
Примером устойчивого движения может служить прохождение корабля по фарватеру при наличии сноса или дрейфа. Опытный рулевой удерживает курс корабля на створе.
САУ называется устойчивой, если после окончания действия на нее внешних сил выходное воздействие 
не будет превосходить невозмущенное воздействие на величину :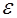 
.
Разность между текущим значением напряжения на входе ИУ и заданным значением напряжения, взятая по модулю, называется отклонением САУ и обозначается:
Заданный диапазон изменения выходного воздействия 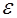называется точность САУ.
Если выполняется условие 
(предел отклонения 
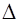стремится к нулю при 
), то система называется асимптотически устойчивой.
ВЫВОД: система будет устойчивой при выполнении следующего условия: 
.
|
|
|
