Квантовых систем во времени

При сопоставлении рассмотренных картин эволюции прежде всего следует заметить, что если в начальный момент времени t₀=0 в координатном представлении имеем и , т.е. совпадают как волновые функции, так и операторы физических величин в картинах движения Шредингера и Гейзенберга, то в последующие моменты времени обнаруживаются две различные ситуации: в представлении Шредингера зависимость от времени перенесена на волновую функцию , а в представлении Гейзенберга - на операторы .

Эквивалентность обоих методов описания следует и из равенства матричных элементов эрмитовых операторов в шредингеровской и гейзенберговской картинах временной эволюции.

Действительно, в картине эволюции Шредингера в координатном представлении матричный элемент оператора A для любых двух состояний и равен:

(15.4)

Используя унитарное преобразование (14.4), запишем

(15.5)

где и 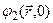- волновые функции соответственно тех же двух состояний в гейзенберговской картине эволюции системы во времени.

С учетом выражений (15.5) матричный элемент (15.4) преобразуется к виду:

(15.6)

т.е.

(15.6`)

Матричные элементы операторов определяют физически наблюдаемые величины, поэтому не могут быть различными в эквивалентных представлениях (о чем свидетельствует вывод уравнения (14.5)). Другими словами, физические результаты должны входить в математический аппарат квантовой механики как унитарные инварианты.

Таким образом, требование унитарной инвариантности соответствующих результатов может служить дополнительным критерием правильности сформулированных ранее (глава 2, §5) основных постулатов (аксиом), положенных в основу квантовой механики.

Гейзенберговская картина эволюции обладает тем преимуществом, что позволяет выявить математическую аналогию квантовой механики и классической механики. Именно в представлении Гейзенберга квантовомеханические соотношения имеют вид классических соотношений, в которых физические величины заменены соответствующими операторами. Особенно широко применяется гейзенберговское представление в квантовой теории поля.

Для практических расчетов удобнее всего пользоваться шредингеровской картиной эволюции, в которой операторы A, сопоставляемые классическим динамическим переменным, не зависят от времени. Всю информацию о временном развитии системы несет волновая функция , удовлетворяющая волновому уравнению Шредингера (14.6). В большинстве случаев решить дифференциальное уравнение (14.6) значительно легче, чем найти решение матричных уравнений Гейзенберга.

Помимо гейзенберговского и шредингеровского представлений часто применяется представление взаимодействия, введенное Дираком. В представлении Дирака в общем случае операторы и векторы состояний явно зависят от времени.

Это представление удобно, когда в гамильтониане H задачи можно выделить малую часть V так, что

(15.7)

где не зависит от времени; оператор V, называемый оператором возмущения, может зависеть и от времени.

В конкретных расчетах оператор описывает, например, систему невзаимодействующих частиц (электронов в атоме гелия), а оператор V учитывает их взаимодействие. Это представление очень удобно при использовании одного из приближенных методов квантовой механики - теории возмущений (стационарной, когда , и нестационарной - ). Очень часто представление взаимодействия используется в квантовой электродинамике.

Наиболее же общая форма описания состояния квантовых систем (гейзенберговская картина эволюции) основана на использовании оператора матрицы плотности , удовлетворяющего уравнению фон Неймана (15.3). Преимущество этого метода описания состоит в единообразном рассмотрении чистых и смешанных состояний квантовых систем.

 

Принцип причинности

К числу основных принципов в физике принадлежит и принцип причинности, согласно которому начальное состояние системы при известном взаимодействии между ее частицами определяет состояние системы в любой последующий момент времени.

В классической механике Ньютона состояние системы однозначно задается каноническими переменными: обобщенными координатами и обобщенными импульсами. Зная характер полей, в которых движется система, с помощью основных дифференциальных уравнений динамики по состоянию системы () в начальный момент времени можно однозначно определить состояние системы () в любой последующий момент времени.

Таким образом, состояние системы в момент времени t₀ и закон взаимодействия ее частиц между собой и с внешними телами могут рассматриваться как причина, а состояние системы в последующий момент t времени - как следствие. В этом заключается существо представлений о динамической или однозначной причинности, получившей название классического детерминизма. Классический детерминизм, не учитывающий элементов случайности, приводит к динамическим закономерностям.

Квантовая механика принципиально статистическая теория, которая в любом представлении позволяет вычислять распределение вероятностей значений любой физической величины, характеризующей систему. Так, например, в шредингеровской картине временной эволюции квантовой частицы ее состояние полностью определяется волновой функцией (координатное представление), квадрат модуля которой равен плотности вероятности нахождения частицы в точке с координатами x,y,z в момент времени t:

Зная волновую функцию, можно вычислить распределение вероятностей значений любой динамической переменной: для этого достаточно разложить в ряд по собственным функциям эрмитова оператора соответствующей величины, при этом квадраты коэффициентов разложения представляют собою вероятности дозволенных значений этой физической величины.

Волновая функция удовлетворяет квантовому уравнению движения Шредингера (14.6), которое позволяет определить в любой момент времени t по заданной начальной функции , если известен гамильтониан H, зависящий от взаимодействия частиц системы.

Следовательно, при заданном гамильтониане H начальное состояние системы, характеризующееся волновой функцией , можно рассматривать как причину, а состояние в произвольный момент времени t с волновой функцией - как следствие. Вероятностный смысл волновых функций, причинно связанных уравнением движения Шредингера (14.6), позволяет сделать вывод о наличии новой формы причинности, которая получила название вероятностной причинности.

Математическим выражением вероятностной причинности в различных представлениях является соответствующее квантовое уравнение эволюции системы во времени (13.7; 14.6; 15.3). Понимание причинности остается прежним: состояние системы в данный момент времени при известном гамильтониане определяется прошлым системы, но способ самого описания состояния становится вероятностным, что приводит к статистическим законам.

Статистические закономерности с присущей им вероятностной формой причинности более глубоко отображают объективные связи в природе, чем классический детерминизм и динамические закономерности.

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: