 |
Спектр значений энергии гармонического осциллятора.
|
|
|
|
Основная задача заключается в определении спектра значений энергии гармонического осциллятора. Исходным является уравнение:
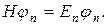(17.1)
Потенциальная энергия гармонического осциллятора равна 
, где 
-собственная частота колебаний, а кинетическая энергия есть 
. Следовательно, гамильтониан осциллятора запишется в виде:
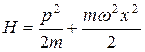(17.2)
Поскольку потенциальная энергия обращается в бесконечность при 
, то гармонический осциллятор может совершать лишь финитное движение (в ограниченной области пространства). В соответствие с этим энергетический спектр осциллятора дискретен.
Из вида операторов 
и 
следует, что 
.
Существует несколько способов решения данной задачи:
1) координатное представление;
2) импульсное представление;
3) матричный метод;
4) операторный метод.
Из всех перечисленных подходов к решению задач операторный метод является наиболее общим, позволяющим перейти к описанию квантованных полей. В операторном методе для определения спектра значений энергии гармонического осциллятора используются лишь перестановочные соотношения для канонически сопряжённых переменных 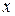и 
:
.
Универсальность теории гармонического осциллятора и её независимость от физической природы станет очевидной после перехода к безразмерным переменным 
и 
:
Заметим, что для гармонического осциллятора частоты имеется единственная величина, имеющая размерность энергии 
, а так как 
имеет размерность энергии, то 
Найдём вид оператора 
. 
имеет размерность энергии, т.е. 
, откуда можно записать, что 
или
(17.3)
Аналогично 
, откуда
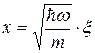(17.4)
Гамильтониан такой системы будет иметь вид:
(17.5)
Тогда оператор примет вид: 
.
Запишем уравнения осциллятора для переменных и :
|
|
|
Откуда 
, 
или 
. Эта переменная подчиняются дифференциальному уравнению первого порядка, т.к.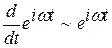 
.
Целесообразно ввести новую переменную b(t): 
. В квантовой механике ей соответствует оператор:
(17.6)
Сопряжённый ему оператор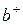 
имеет вид:
(17.7)
Оператор не эрмитовский. Покажем это. Установим перестановочные соотношения для вновь введённых переменных b и 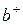и запишем гамильтониан гармонического осциллятора в этих переменных.
т.е.
(17.8)
Т.к. ,то 
. Подставив полученный результат в (17.8) получим:
. (17.9)
Выразим и через 
и 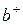. Получим:
(17.10)
. (17.11)
Откуда определим гамильтониан гармонического осциллятора:
Из соотношения (17.9) следует соотношение
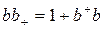, (17.12)
учитывая которое гамильтониан примет вид
или
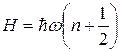, (17.13)
где оператор n есть
. (17.14)
Обозначим собственные значения оператора n через 
и рассмотрим следующие уравнения на собственные функции и собственные значения:
.
Откуда, учитывая (17.12), получим
. (17.15)
Таким образом, наша задача свелась к нахождению собственных значений оператора n.
Прежде всего докажем, что не могут быть отрицательными. Для этого рассмотрим уравнение:
.
Умножая скалярно левую и правую части равенства на 
и учитывая условие нормировки для векторов , получим:
.
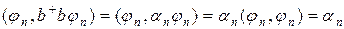С другой стороны, учитывая, что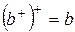 
:
.
Таким образом, 
.
Далее установим две вспомогательные леммы.
Лемма1: Если - собственные вектора с собственными значениями , то вектор 
также является собственным вектором оператора с собственным значением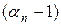 
, т.е.
. (17.16)
Доказательство: Учитывая равенства (17.12), (17.14), (17.15) запишем
Таким образом, лемма доказана.
Лемма2:Если - собственный вектор оператора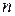 
с собственным значением , то вектор 
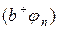также является собственным вектором оператора 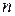с собственным значением 
, т.е.
(17.17)
Доказательство: Учитывая равенства (17.14), (17.12), (17.15) получим
что и требовалось доказать.
Отсюда имеем собственные вектора состояния 
, которым соответствует минимальное собственное значение 
, т.е. 
. Согласно лемме1, 
также является собственным вектором оператора :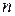
|
|
|
,
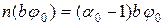но - минимальное собственное значение оператора и 
. Следовательно, 
, откуда 
или 
.
Так как собственные значения , согласно леммам 1 и 2, отличаются друг от друга на единицу, то =0,1,2,…n. Обозначим и запишем леммы 1 и 2 с учётом вновь введённого обозначения:
(17.16`)
(17,17`)
Откуда следует, что 
и 
можно записать в следующем виде:
и 
найдём из условия нормировки:
Рассмотри скалярное произведение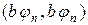 
:
.
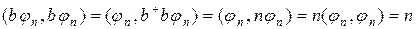С другой стороны,
Таким образом, 
и
. (17.18)
Аналогичным образом находим , откуда
. (17.19)
Таким образом, собственные значения оператора Гамильтона примет вид:
, (17.20)
где n=0,1,2,…
Из соотношения (17.20) следует, что минимальное значение энергии гармонического осциллятора отлично от нуля 
и спектр энергии гармонического осциллятора эквидистантен.
Применим полученный результат к некоторым примерам, рассмотренным в начале параграфа.
1). Электромагнитное поле эквивалентно совокупности независимых гармонических осцилляторов. Для любого такого осциллятора спектр значений энергии имеет вид:
.
Так как осцилляторы независимы, то спектр значений энергии свободного электромагнитного поля равен сумме возможных значений энергий гармонического осциллятора:
где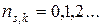 
Выясним физический смысл оператора n. Монохроматической волне 
ставится в соответствие кванты поля 
. Тогда в выражении для энергии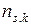 
приобретает смысл числа фотонов в состоянии 
, при этом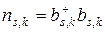 
есть оператор числа фотонов в состоянии . Из соотношений же
следует, что 
есть оператор уничтожения фотона в состоянии 
, а 
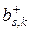-оператор рождения фотона в состоянии .
2). Колебания кристаллической решётки есть совокупность независимых гармонических осцилляторов. Таким образом, 
, где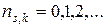 
. Упругой волне в кристалле ставится в соответствие квант-фонон. Тогда 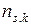- оператор числа фононов.
|
|
|
