 |
Стационарные состояния гармонического осциллятора. Координатное, импульсное и матричное представления.
|
|
|
|
Проанализируем особенности стационарных состояний гармонического осциллятора в различных представлениях.
Координатное представление.
Для нахождения стационарных состояний гармонического осциллятора воспользуемся стационарным уравнением Шредингера:
.
Введём безразмерные переменные 
и 
. Откуда, согласно (17.6):
. (18.1)
Используя равенство (17.19), найдём 
, а затем 
:
Аналогично:
(18.2)
Определим вид собственной функции 
, для чего воспользуемся соотношением:
(18.3)
Постоянную C найдём из условия нормировки:
Откуда
и согласно выражению (18.3)
. (18.4)
Воспользуемся соотношением (18.1) для нахождения вектора 
:
т.е.
(18.5)
где 
- полином Чебышева-Эрмита:
(18.6)
или в развёрнутом виде:
(18.6`)
Из последних соотношений очевидно, что состояния гармонического осциллятора могут быть как чётными, так и нечётными.
Импульсное представление.
По аналогии с выше рассмотренным представлением, определяя операторы 
и 
следующим образом:
,
, (18.7)
получим следующие выражения для волновых функций стационарных состояний гармонического осциллятора в импульсном представлении:
(18.8)
Матричное представление.
Согласно (17.4) и (17.10):
. (18.9)
Найдём матричные элементы оператора 
.
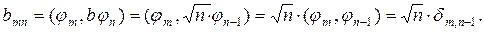
Откуда,
.
Найдём минимальное n: n-1=0, n=1.
Таким образом, матрица оператора b примет вид:
(18.10)
Матрица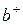 
получится путём транспонирования, т.е. путём замены строчек на столбцы:
(18.11)
Подставляя (18.10) и (18.11) в (18.9) находим вид оператора координаты в матричном представлении:
(18.12)
Аналогично, используя соотношения (17.3), (17.11), можно получить вид оператора импульса в матричном представлении.
Глава VII. Квантовая теория момента.
Наряду с энергией и импульсом момент количества движения относится к фундаментальным физическим величинам, связанным с наиболее общими свойствами пространства-времени. Из однородности пространства-времени следует сохранение энергии-импульса для замкнутой системы. Изотропность пространства (симметрия относительно вращения) приводит к сохранению момента количества движения.
|
|
|
В квантовой механике моменту количества движения отводится особое место в силу его специфических квантовых свойств.
Общие свойства и особенности квантового момента.
При построении квантовой теории момента количества движения воспользуемся принципом соответствия, согласно которому каждой физической величине ставится в соответствие линейный эрмитов оператор
Следовательно, соотношения между физическими величинами в классической теории должны перейти в соотношения между операторами физических величин в квантовой механике. В частности, классическим скобкам Пуассона
(19.1)
ставится в соответствие квантовые скобки 
:
(19.2)
Это своеобразное применение принципа соответствия между классической и квантовой механиками оказалось очень плодотворным.
Учитывая выражение момента импульса
,
с помощью (19.1) можно получить следующие классические соотношения:
Откуда, согласно принципу соответствия, сопоставив классическим скобкам Пуассона квантовые, получаем следующие соотношения для квантово-механического момента импульса 
т.е. согласно (19.2)
(19.3)
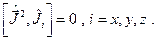(19.4)
Из соотношений (19.3) и (19.4) следует, что одновременно измеримыми величинами являются квадрат момента и одна из его проекций. В качестве последней примем 
:
.
Геометрически это можно представить с помощью так называемого «конуса состояния» (рис. 1).
Рис. 1. «Конус состояния». Одновременно точные значения могут иметь лишь величины и 
.
|
|
|
