Законы сохранения (интегралы движения) в квантовой механике

В классической механике при исследовании движения систем частиц важную роль играют первые интегралы движения. Среди них есть несколько таких интегралов движения, постоянство которых имеет глубокое происхождение, связанное с симметрией времени и пространства - их однородностью и изотропностью. Эти интегралы движения, имеющие вид

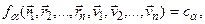(16.11)

(где 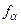- некоторая функция радиусов-векторов и векторов скоростей 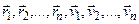частиц свободной механической системы, 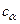- константа), выделяют в особую группу и называют законами сохранения. Помимо связи законов сохранения с симметрией пространства и времени есть еще ряд причин, выделяющих эти интегралы движения в особую группу. Во-первых, все сохраняющиеся величины типа (16.11) обладают свойством аддитивности, т.е. значения указанных величин для системы невзаимодействующих между собой частиц равно сумме тех же величин для каждой частицы в отдельности. Во-вторых, если любые первые интегралы движения можно записать лишь на основе анализа дифференциальных уравнений движения, то о законах сохранения для механической системы можно судить по наиболее общим признакам (принадлежность системы к определенному классу механических систем). К ним прежде всего относятся законы сохранения энергии, импульса, момента импульса. Эти физические величины называются универсальными динамическими переменными и широко используются в физике при рассмотрении разнообразных явлений.

В классической физике указанные законы сохранения получают с помощью теории об изменении со временем энергии, импульса, момента импульса. С помощью этих теорем рассматриваются специальные условия, при которых данные величины не изменяются во времени, т.е. сохраняются. Такими условиями, например, служат замкнутость (изолированность) изучаемой системы или симметрия внешнего силового поля.

В квантовой механике подход к законам сохранения основывается на квантовых уравнениях движения (13.7):

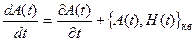
Из него следует, что при выполнении условия

(16.12)

среднее значение величины A(t) сохраняется во времени:

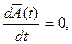(16.13)

т.е. - интеграл движения.

Особый интерес представляет случай, когда оператор физической величины явно не зависит от времени:

(16.14)

Тогда (16.12) принимает вид:

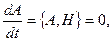(16.15)

т.е. физическая величина 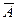будет являться интегралом движения, если ее оператор A коммутирует с гамильтонианом H системы.

Рассмотрим условия сохранения определенного значения физической величины. Если для оператора физической величины A выполняется условие (16.12) и одна из собственных функций 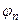этого оператора совпадает с функцией состояния, в котором находится система, то определенное значение A_n этой системы сохраняется. В этом случае из формулы для среднего и условия (16.13) получаем:

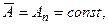(16.16)

т.е. определенное значение A_n физической величины является интегралом движения.

Закон сохранения энергии.

Для энергии E - одной из универсальных динамических переменных - опратором является гамильтониан H, который может зависеть явно от времени, но может и не зависеть от него. В случае стационарных полей . Кроме того, очевидно, что квантовые скобки Пуассона в этом случае всегда равны нулю:

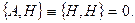(16.17)

Следовательно, 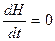, т.е. .

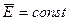Если функция состояния системы, находящейся в стационарном поле, является собственной для гамильтониана H, то энергия имеет определенное сохраняющееся значение. Такие состояния, как известно, называются стационарными.

Таким образом, энергия микрочастицы в стационарном поле сохраняется.

В случае свободной частицы гамильтониан ее 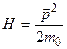явно не зависит от времени и t, откуда следует: энергия свободно движущейся частицы сохраняется.

Важным случаем является замкнутая система. Замкнутость системы означает, что потенциальная энергия взаимодействующих между собой частиц ее зависит только от расстояний между ними. Но гамильтониан системы явно не содержит времени, поэтому энергия замкнутой системы микрочастиц сохраняется.