 |
Законы сохранения в квантовой механике
|
|
|
|
Пусть 
не содержит обращения во времени и является преобразованием симметрии. Представим, что есть сколь угодно малое значение 
, которое определяет :
,
где 
- эрмитовский оператор.
Если разложить значение оператора 
в ряд, то получится:
,
т.е. преобразование отличается от тождественного на бесконечно малую величину. - унитарное преобразование и для него выполняется два условия симметрии, отсюда следует, что – преобразование симметрии.
Рассмотрим теорему.
Теорема: Если имеется сколь угодно малое преобразование симметрии, то имеется сохранение величины 
.
Доказательство:
.
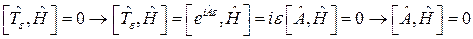Имеет место также обратная теорема.
Теорема обратная: Пусть - интеграл движения, тогда мы можем построить унитарный оператор симметрии.
Доказательство:
.
Рассмотрим примеры.
Пусть имеется замкнутая система, в которой интегралами движения являются энергия 
, обобщенный импульс 
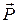, момент количества движения 
. Тогда мы можем сделать вывод о том, что время в системе однородно, а пространство однородно и изотропно.
Покажем это.
1) - интеграл движения и 
- преобразование симметрии, т.е. 
однородность во времени;
2) 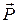- интеграл движения и 
- преобразование симметрии, т.е.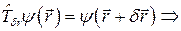 
однородность в пространстве;
3) - интеграл движения и 
- преобразование симметрии, т.е. 
изотропность в пространстве.
А теперь рассмотрим, как используется симметрия для решения конкретных задач.
Трансляционная симметрия кристаллических тел.
Функции Блоха
Вся квантовая механика инвариантна относительно унитарных операторов. Некоторые из них оставляют инвариантными уравнения движения. Эти операторы есть преобразования симметрии.
Если преобразования симметрии не затрагивают время, то симметрии этой физической системы означает инвариантность гамильтониана системы, т.е. 
.
|
|
|
В физике кристаллические тела обладают повышенной симметрией. Для них характерен определенный порядок в кристалле.
Выделим в кристалле направление 
, где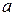 
- период решетки. При трансляции на вектор 
, где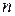 
- целое число, кристалл совмещается сам с собой.
Все спектры энергии возбуждения кристалла определяются трансляционной симметрией.
Рассмотрим простейшую ситуацию одномерного кристалла. Состояние системы определяется уравнением Шредингера: 
. Введем оператор симметрии 
(кристалл не меняется при трансляции на период решетки 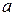), т.е. 
.
А так как оператор трансляции и гамильтониан коммутируют, т.е. 
, следовательно, они имеют полную систему общих собственных векторов:
Нужно найти собственные вектора и собственные значения оператора симметрии для того, чтобы подставить их в уравнение Шредингера и найти оттуда спектр энергии 
в кристалле.
Обратим внимание на то, что 
комплексная функция, и поэтому ее можно представить в виде:
,
где 
- действительные функции.
Рассмотрим, чему равна плотность вероятности 
:
,
так как трансляция на вектор не меняет кристалл. Это возможно тогда и только тогда, когда 
- периодическая функция, т.е. 
.
Мы ищем решения в виде:
.
Подставляем это решение в уравнение 
:
.
Отсюда следует, что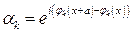 
.
Представим 
в виде ряда:
,
в определенной системе отсчета можно задать 
.
Подставляя значение 
в выражение для собственного значения оператора трансляции , получаем:
где 
- действительное число, 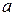- период решетки.
- функция периодическая:
,
где 
- вектор обратной решетки.
Квантовое число можно задать в пределах этого периода: 
, называемого элементарной ячейкой обратной решетки.
Таким образом, собственное значение оператора трансляции есть периодическая функция с периодом обратной решетки.
|
|
|
Исходя из этого, можно сделать вывод, что энергия в кристалле тоже периодическая функция с периодом обратной решетки:
.
При данном значении могут быть, вообще говоря, несколько значений энергии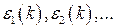 
.
При трансляционной симметрии в таком кристалле состояние описывается формулами Блоха, которые определяются произвольной периодической функцией и выражаются через период решетки или через квазиимпульс:
или 
.
Функция Блоха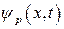 
запишется так:
.
Учтем тот факт, что энергия в кристалле есть периодическая функция 
и четная относительно обращения во времени 
.
[1] Стефан установил этот закон в 1879г. на основании опытных данных, а в1884г. Больцман получил этот закон, исходя из второго начала термодинамики.
[2] На опыте обычно измеряют не, а энергию, излучаемую в 1с черным телом с 1 см2 его поверхности в одну сторону, в этом случае, откуда, т.е. зная, вычисляют.
[3] Предложенный первоначальный вывод формулы Планка страдает рядом недостатков. При рассуждениях непоследовательно соединялись противоречивые понятия осцилляторов и стоячих волн в полости
[4] За работы по вопросам квантовой механики М. Борну в 1954 г. присуждена Нобелевская премия.
[5]Сложность эксперимента обусловлена тем, что дебройлевская длина волны электронов существенно меньше длин волн видимого света.
[6] Система собственных векторов является ортогональной и полной не только для эрмитова оператора, но и для операторов более широкого класса.
[7] Плоские монохроматические волны де Бройля (5.1), описывая состояние идеализированного объекта (свободной частицы), являются векторами унитарного пространства, т.к. их норма не равна 1; но суперпозиция таких векторов даёт волновые пакеты, представляющие векторы Г–пространства.
1 Как уже отмечалось, в квантовой механике используются векторы Г-пространства с расширением, т.е. векторы, норма у которых равна 1, и векторы, которые нормируются на d-функцию Дирака.
1 Для случая частицы, движущейся с заданным вектором импульса, волновая функция
[8] По определению сопряжённого оператора, если то
[9] Термин «представление» здесь используется в более широком смысле: в смысле картины эволюции во времени квантовой системы. Этот термин часто используется в более узком смысле: координатное, импульсное, энергетическое и т.д. представления.
|
|
|
[10] Оператор матрицы плотности зависит от некоторых переменных, например, в координатном представлении от координат. В связи с этим при дифференцировании по времени использован знак частной производной.
|
|
|
