Главная | Обратная связь | Поможем написать вашу работу!

Самостоятельная работа № 37

Уравнение касательной

Цель: решить задачи на уравнение касательной

Источники информации:

1. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студ. Учреждений сред. Проф. Образования. – М.: Издательский центр «Академия», 2016. – 256с.

2. Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачёва и др. Алгебра и начала математического анализа 10-11 классы. – 16-е изд., перераб. – М.: Просвещение, 2010.- 464с.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ

Касательной к графику функции f(x) в точке х_о называется прямая, заданная уравнением y = f(x_о) + f ꞌ(x_о)(x-x_o), f ꞌ(x_o) = k = tg α.

Значение производной функции в точке х_о равно угловому коэффициенту касательной к графику функции в этой точке.

Пример:

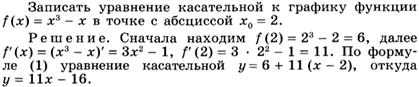
Задание

Пользуясь методическими рекомендациями, выполнить задания.

Дана функция y=f(x). Найдите:

1) угловой коэффициент касательной к графику этой функции в точке с абсциссой х_о;

2) точки, в которых угловой коэффициент касательной равен k;

3) напишите уравнение касательной к графику функции в точке с абсциссой х_о:

1.		5.
2.		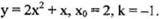6.
3.		7.
4.		8.

Формат выполнения: решение упражнений

Форма сдачи отчетности: решённые задания

Самостоятельная работа № 38

Правила дифференцирования

Цель: решить задачи на применение правил дифференцирования

Источники информации:

2. Ш..А. Алимов, Ю.М. Колягин, М.В. Ткачёва и др. Алгебра и начала математического анализа 10-11 классы. – 16-е изд., перераб. – М.: Просвещение, 2010.- 464с.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ

Для нахождения производной функции необходимо воспользоваться:

- таблицей производных;

- правилом нахождения производной сложной функции;

- основными формулами (производная суммы, произведения, частного).

Пример: Найти производную функции

Решение:

Задание

Пользуясь методическими рекомендациями, выполнить задания.

Найдите производную функции:

1.		7.
2.		8.
3.		9.
4.		10.
5.		11.
6.		12.

Формат выполнения: решение упражнений

Форма сдачи отчетности: решённые задания

Самостоятельная работа № 39

Промежутки монотонности и экстремумы функции

Цель: решить задачи на промежутки монотонности и экстремумы функции

Источники информации:

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ

Для решения неравенств f ꞌ(x)>0 и f ꞌ(x)<0 удобно пользоваться обобщением метода интервалов (теорема Дарбу): точки, в которых производная равна 0 или не существует, разбивают область определения функции f(x) на промежутки, в каждом из которых f ꞌ(x) сохраняет постоянный знак.

Для нахождения точек максимума и точек минимума удобно пользоваться упрощённой формулировкой признака:

- если в точке х_о производная меняет знак с минуса на плюс, то х_о есть точка минимума;

- если в точке х_о производная меняет знак с плюса на минус, то х_о есть точка максимума.

Пример:

1.	: ^:
2.

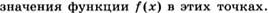
Задание

Пользуясь методическими рекомендациями, выполнить задания.

Найдите промежутки монотонности функции:
1.		4.
2.		5.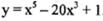
3.		6.
Найдите точки экстремума функции:
7.		10.
8.		11.
9.		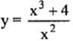12.