 |
Математический диктант (зрительный на карточках).
|
|
|
|
5:5, 20:5, 36:6, 81:9, 64:8, 49:7, 5*1, 2*5, 21:7, 2*1.
Задания: 1) работа в парах – взаимопроверка;
2) Работа с числовым рядом.
1, 2, 3, 4,5, 6, 7, 8, 9, 10.
- проблемный вопрос: могут ли эти числа составить натуральный ряд? (да)
- на какие группы можно разбить эти числа? (четные – нечетные, однозначные – двузначные)
У.М. Мне бы очень хотелось узнать названия этих чисел на английском.
Повторение количественных числительных 1-10.
Игра с мячом, составляем словосочетания вида – количественное числительное + существительное во множественном числе. Слова: a cat, a pig, a hen, a pen, a rabbit, a fox, a pencil-box, a ruler, a rubber, a bag, a cow, a cockerel, a stick, a pencil.
6. Чтение - Reading (учебник, с.79, у.3,4 – найдите словосочетания и предложения с числами).
Следующий урок – PE. (физкультминутка)
One, one, one – little dogs run.
Two, two, two – cats see you.
Three, three, three – birds in a tree.
Four, four, four – rats on the floor.
Работа с интерактивной доской.
Найди значение выражения:
| 6 * 2 + (13 – 5) = (40) 36: 6 + 24: 6 = (30) 4 * 2 + 8 * 4 = (20) 6 * 6 – 18: 3 = (10) | 27: 1 - 2 * 3 = (21) 5 * 6 – 21: 3 = (23) 5 * 9 - 4 * 5 = (25) |
- работа по цепочке, расставить порядок действий и записать значения выражений на интерактивной доске;
- выявление закономерностей – что общего в значениях выражений каждого столбика? (в первом столбике круглые числа, записаны в порядке возрастания, во втором столбике двузначные числа, записаны в порядке убывания; количество десятков равняется двум).
У выражений появляются английские буквы: S R U N M B E. Задание: запиши ответы в таблицу в порядке возрастания. (Получается слово NUMBERS).
У.М. Ребята, объясните происхождение названий двузначных чисел в русском языке.
У.А. А я вас хочу познакомить с названиями этих чисел в английском языке.
|
|
|
Работа с модулями.
- модуль – введение новой лексики
- модуль – игра на закрепление слов (угадай слово)
Итог урока.
На «страницу дневника» вывешиваются красные пятерки за пройденные «уроки».
У.М. В каких жизненных ситуациях нам пригодятся знания, полученные на уроке? Все ли предметы в школе связаны между собой? Есть ли связь между английским языком и математикой?
«Решение треугольников» 9 класс
Авторы: Братищева А.С., учитель математики
Копылова Л. А., учитель английского языка
Ход урока.
1 этап.
Организационный момент.
Ребята, сегодня у нас необычный урок – урок математики и английского языка. Мы будем повторять решение треугольников и узнаем о выдающихся ученых Великобритании и их вкладе в развитие математики.
В начале краткая историческая справка о том, чем вызвано «решение треугольников».
Начиная с древних времен, людей интересовало решение треугольников, т.е. вычисление одних элементов треугольника по другим его элементам.
Для решения треугольника необходимо иметь три независимых соотношения между его элементами.
В Евклидовой геометрии одно из них выражается равенством 
.
Помимо этого равенства используется теорема синусов и теорема косинусов. Теорема косинусов была доказана еще в «Началах» Евклида, в которой обобщается теорема Пифагора. Однако впервые теорема косинусов была сформулирована (словесно) в 16 веке французским математиком Франсуа Виетом.
Жак Лагранж вывел в 1779 году теорему синусов из теоремы косинусов. Эти две теоремы и равенство позволяют решить любой треугольник.
Все эти вычисления были вызваны запросами астрономии, географии, мореплавания, архитектуры, топографии, геодезии, измерительными работами на местности.
|
|
|
В настоящее время вычисления находят применение для нахождения расстояния до недоступной точки, вычисления угла попадания мяча в ворота, измерения высоты предмета; в физике – для нахождения величины равнодействующей силы и т.д.
2 этап.
Устное задание.
Look at these mathematical signs and say what they mean
| + | - | ± | · | : | = | ≠ | ≈ | > | < | ≥ | ≤ | √ |
3 этап.
Решите тестовые задания, выберите правильный ответ и узнайте фамилию великого английского ученого. Прочтите эту фамилию, заполнив таблицу.
1) В треугольнике PQR PQ=7,2 см, QR=3,6 см, RP= 4,9 см. Какой угол треугольника наибольший? P) 
QPR C) 
PQR R) QRP
2) В треугольнике ABC A=46 
, B=75 
. Какая сторона треугольника наименьшая? H) AB D) CA E) BC
3) В треугольнике BC = a, CA=b и S - площадь этого треугольника. Тогда: K) S=absinС T) S=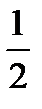 
abcosС C) S= 
absinС
4) В треугольнике KMP KM=4, MP=5, а его площадь равна 5. Найдите синус угла М. O) G) 2 A) 
.
5) Пусть R – радиус окружности, описанной около треугольника ABC. Тогда: K) BC=2RsinB R) BC=2RsinA E) DC=RsinA
6) Треугольник ABC вписан в окружность. Известно, что BC = 2, CAB =30 . Определите радиус окружности. D) 2 L) T) 4.
7) Пусть в треугольнике ABC AB = c, BC= a, CA= в. Тогда:
O) 
A)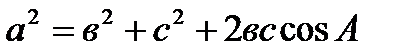 
E) 
Заполнение таблицы:
| №1 | №2 | №3 | №4 | №5 | №6 | №7 |
| QRP
| BC | S= absinС
|
| BC=2RsinA | 2 |
|
| R | E | C | O | R | D | E |
4 этап.
Решите устно по-английски (См. рисунок)
Ответ:
Нет решений,
треугольник со сторонами 2,3,6 не существует,
т.к. 2+3<6.
5 этап.
Следующий этап – работа творческих групп на просторах страны «Решение треугольников».
Всего 3 группы, задания дифференцированы по степени сложности.
Группа 1.
1. Стороны треугольника 3см, 4 см и 6 см. Определите вид этого треугольника.
2. Стороны треугольника 7см, 8 см и 10 см. Определите вид этого треугольника.
3. Стороны треугольника 7см, 9 см. Может ли угол, противолежащий стороне 7 см, быть тупым?
4. В треугольнике АВС АВ=8 см, ВС=12 см. Может ли синус угла С равняться 0,8?
Варианты ответов:
1. остроугольный
2. прямоугольный
3. тупоугольный
4. может
5. не может
Группа 2.
1. Стороны треугольника 7см, 8 см и 10см. Найдите косинус наибольшего угла этого треугольника.
2. В треугольнике АВС АВ=5, АС=12, С=30 . Найдите синус угла В.
3. В треугольнике АВС СВ=4, АС=2, В=50 , А=70 . Найдите АВ.
|
|
|
4. Стороны треугольника равны 0,2 см, 0,39 см и 0,48 см. Синус угла, противолежащего большей стороне, равен 0,2. Найдите радиус описанной окружности.
Варианты ответов:
1. 
2. 
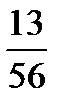
3. 1,2
4. нет решений
5. 3√2
6.18
7. 2√3
Группа 3.
В треугольнике АВМ стороны АВ, ВМ и АМ равны соответственно 6,8 и 10. точка К – середина стороны ВМ, точка С – середина стороны АМ, точка Е – середина ВС.
1. Найдите косинус угла ВСК.
2. Найдите косинус угла ЕСК.
3. Найдите радиус окружности, описанной около треугольника ВСА.
4. Найдите площадь треугольника ЕСА.
Варианты ответов:
1. 0,8
2. 0,6
3. 6
4. 0,28
5. 0,96
6. 3,125
7. 6,25
6 этап.
Учитель математики проверяет самостоятельные работы, а учитель английского языка предлагает выполнить задание по чтению.
Прочитайте небольшие сообщения и переведите их на русский язык.
Предлагаются тексты на английском языке. (См. Приложение №1)
7этап.
А сейчас «Весёлая минутка». Выполните задание №1:
Три слога в слове. Первый слог – большой снеговика кусок.
Осуществляют слог второй слоны, придя на водопой.
А третий слог зовётся так, как раньше звался твёрдый знак.
Соедини все три как надо. Получишь ЭВМ в награду.
Ответ: Ком-пьют-ер.
Выполните задание №2: What is the longest word in English?
Ответ: SMILES (because there is a mile between the letters s) [10].
8этап.
Домашнее задание.
Подготовьте сообщение на английском языке (на выбор):
- о Франсуа Виете;
- о Жаке Лагранже.
9этап.
Итоги урока
– Что связывает математику и иностранный язык?
– Нужны ли знания, которые мы получаем по математике, при изучении иностранного языка?
– Мы учим язык, на котором говорили учёные, которые совершили так много открытий в математике.
Рефлексия.
У каждого ученика в начале урока лежали на столах смайлики. В конце урока они сдали учителю тот смайлик, который соответствовал их настроению.
| Мне всё понятно. Вопросов нет. | Мне ничего не понятно. | У меня есть вопросы. |
|
| 
|
Приложение №1
– Every country is proud of its people who made the country famous and brought it glory. Great Britain is one of such countries. Its outstanding writers and poets, statesmen and politicians, musicians and scientists are well-known all over the world. Now we are going to read about Britain’s famous scientists who made their contribution into mathematics.
Task 1: read the texts and complete the chart.
Task 2: read the texts again and say which two scientists the sentences refer to.
|
|
|
Robert Recorde was born in Tenby, Wales in 1510. Unfortunately we know little about his childhood. As a young adult he studied at Oxford, then at Cambridge where he graduated in medicine. Recorde wrote many books in mathematics. He first used the symbols (+) and (–). Recorde is credited for developing the (=) equal sign. Recorde died in the
King’s Bench Prison in 1558, where he was committed for debt [6].
Isaac Newton, one of the greatest scientists of all times was born in 1642 in a little village in Lincolnshire, England. After school he studied maths at Cambridge University and received his degree in 1665. Newton made three great discoveries – the discoveries of the differential calculuses; the nature of the white light and of the law of gravitation. Newton died at the age of 84 and buried in Westminster Abbey [6].
Thomas Harriot (1560–1621) was an English scientist and mathematician.
He was born in Oxfordshire, England, in 1560. Little is known about his parents. In 1557 Harriot entered the University of Oxford.
He studied optics, astronomy and geometry. Thomas Harriot invented the signs for “greater than” (>) and “less than” (<) in use today [7,8].
Which two scientists do the sentences refer to?
-They studied at Oxford.
- They were born in England.
-Little is known about their childhood.
- They studied physics.
Complete the chart
| Mathematician | Year and plage of birth | Plage of study | Contribution into maths |
| Robert Recorde | 1510 | Oxford | He was the first to use the sumbols (+) and (-). He developed the (=) equal sign. |
| Isaac Newton | 1642 | Cambridge | He discovered the differential calculuses. |
| Thomas Harriot | 1560 | Oxford | He invented the signes for “greater than” (>) and “less than” (<) |
«Арифметическая прогрессия» 9 класс
Ход урока
Учитель математики - Здравствуйте!
Учителя английского языка –Good morning!
Сегодня у нас нетрадиционный урок- урок английского языка и математики.
- We are glad to see you at the lesson.Good luck and be at your best.
Учитель математики - Тема нашего урока «Арифметическая прогрессия»
(Демонстрируется слайд)
Не расслабляйтесь как эти котята, мы будем двигаться вперед к познанию нового, ведь «Прогрессия – это движение вперед»
Цели урока
The objectives of the lesson
Повторение материала по теме
«Арифметическая прогрессия»
revision of mathematical terms
использование математических и лингвистических навыков в нестандартных ситуациях
enlargement of mental outlook
involving you into learning process communicating with each other
Учитель английского языка –You know the rule of arithmetical progression in Russian. Now, you’ll get acquainted with the rule in English. You have been given the envelopes with the sentences. The sentences are in disorder. Arrange the sentences in the right order to make up the rule of arithmetical progression in English.
(Учащиеся составляют в группах разрезанный на части текст)
Arithmetic Progression
An arithmetic progression is a sequence in which each term (after the first) is determined by adding a constant to the preceding term. This constant is called the common difference of the arithmetic progression. An arithmetic progression can be defined as follows:
The arithmetic progression { an } = a1, a2, a3,...., an,
where n = 1, 2, 3,...
Its terms are determined by the equation:
an = a1 + (n - 1)d, where
a1 is the first term of the arithmetic progression
an is the nth term of the arithmetic progression
n is the term number
d is the common difference of the arithmetic progression
The sum of the first n terms of an arithmetic progression is
calculated as
Sn = n (a1 + an) / 2
|
|
|
or
Sn = n (2a1 + (n - 1)d) / 2 where an = a1 + (n - 1)d
Учитель английского языка – Let’s check the result of our work. Read the text that you’ve made up.(учащиеся читают текст).Translate the text into Russian(учащиеся переводят текст)
Учитель математики - Вы повторили правила. Теперь заполните таблицу, которая находиться на ваших столах.
(ученики заполняют таблицу и проверяют правильность заполнения при помощи слайда)
Учитель английского языка - Arithmetical progression is closely connected with the name Carl Gauss(демонстрируется слайд)
Now you‘ll be given the text about Carl Gauss. Read the text, be attentive and get ready to complete the tasks after reading the text.
(учащиеся читают текст’ Carl Gauss’)
Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, analysis, differential geometry, geodesy, magnetism, astronomy and optics. Sometimes known as “the prince of mathematicians” and “greatest mathematician since antiquity”, Gauss had a remarkable influence in many fields of mathematics and science and he is one of the most influential mathematicians.
He discovered several important mathematical concepts. He invented modular arithmetic, simplified manipulations in number theory, determined the solution of quadratic equation and his name is connected with arithmetical progression.
A study of his personal diaries reveal that he had discovered several important mathematical concepts, but he never published them. He felt them incomplete. Gauss was a perfectionist and a hard worker. Every concept was later discovered and proved by other mathematicians.
He was a great man and his achievements won’t be forgotten.
Gauss was a child prodigy. He was an only son of uneducated lower-class parents. His father was a brick –layer and wanted his son to follow in his footsteps. Despite hard living conditions Gauss showed his brilliant mind at a young age.
According to the legend, Carl was three when he corrected, in his head, an error his father had made on paper while calculating finances.
Another famous story has it that in primary school his teacher, J.G Buttner tried to occupy the pupils by making them add up the integers from 1 to 100. While his classmates toiled\ усиленно трудиться\ over the addition, Carl sat and pondered \размышлять\the question. The young Gauss produced the correct answer to the astonishment of his teacher and classmates. He invented the shortcut formula on the spot, and wrote down the correct answer.
Учитель английского языка - Now complete the sentences according to the text.
Work individually.
(каждый учащийся в группе получает индивидуальное задание)
Complete the sentence according to the text
1. Gauss contributed significantly to many fields, including…
He is known as…
He discovered several important mathematical …
2.Complete the sentence according to the text
A study of his personal diaries reveal, that he…
several important mathematical concepts, but he ….
He felt them …
Gauss was a perfectionist and…
Complete the sentence according to the text
3. Gauss was a child… His father was…and he wanted his son….Despite hard living conditions…According to the legend Carl was three when…
Complete the sentence according to the text
4. Another famous story has it that in primary school his
teacher JG. Buttner ….While his classmates… Carl… He
… on the spot. He produced…
Учитель английского языка – Numbers one come here.Form a group
Numbers two join each others here. Discuss your tasks in the groups.
(Учащиеся, которые выполняли задание 1 собираются вместе и обсуждают свои ответы, то же делают учащиеся, которые выполняли задания 2, 3, 4)
Учащиеся группы 1 –We’ve discussed the tasks in the group. We have completed the sentences in such a way
Gauss contributed significantly to many fields, including number theory, analysis, differential geometry, geodesy, magnetism, astronomy and optics. …
He is known as… “the prince of mathematicians” and “greatest mathematician since antiquity”,
He discovered several important mathematical … concepts. He invented modular arithmetic, simplified manipulations in number theory, determined the solution of quadratic equation and his name is connected with arithmetical progression.
( Группы 2, 3, 4 рассказывают как они выполнили задание)
Учитель математики -А как же Гаусс решил эту задачу?
Задача очень непроста:
Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Пять первых связок изучи;
Найдешь к решению ключи!
1+ 100=101
2+ 99= 101
3+ 98= 101
4+ 97= 101
5+ 96= 101
Давным-давно сказал один мудрец,
Что прежде надо
Связать начало и конец у числового ряда. 5050
Учитель математики – Давайте, и мы с вами попрактикуемся решать задачи. Справившись с заданием, вы получите математические термины на английском языке.
(ученики в группах решают задачи и заполняя таблицы получают математические термины на английском языке)
1. What is the seventeenth term of the arithmetical progression19, 15,…?
2. Calculate the sum of the first seventeen terms of this progression?
3. The arithmetical progression an has a1=-12 and d =3.
Work out the number of the term that is equal to 0.
4. What is the common difference of the arithmetical progression an if a1=28 and a21=4?
5. The arithmetical progression is defined by the two first terms 3.7; 2.5;…calculate a3, a4
6. The term of the arithmetical progression yn equals 29.4 work out n(the number of the term) if y1=10.2 and d=0.4
7. Work out the sum of the first 10 terms of the arithmetical progression(an) if a1=- 32 and d=5.
Ученики заполняют таблицы
1) a1=19? d=4 a17= 19-4∙16=-45
2) S17=-45+19\2∙17=-221
3) 0=-12+3(n-1)? 12+3=3n? n=5
4) 4=28+20d? d=-1,2
5) d=2,5-3,7=-1,2; a3=1,3; a4=0,1
6) 29,4=10,2+0,4(n-1), n=49
7) S10=(-32∙2+5∙9\2)10=-95
(учитель английского языка – Group number one what word have you got?-(ученики отвечают- equation
Number two- sequence
Number three-constant
Учитель математики - Как мы можем представить суммы записанные в первом столбике строке в виде квадрата числа?
Учащиеся-В первой строке записана сумма арифметической прогрессии.
Представим сумму в виде квадрата чисел 1= 1 в квадрате
1+ 3 = 2 в квадрате
1+ 3+ 5= 3 в квадрате
1+ 3+ 5+ 7= 4 в квадрате
Учитель математики -Как мы можем представить суммы записанные во втором столбике в виде куба числа
Учащиеся 1 это 1 в кубе
3+ 5 = 6 –это 2 в кубе
7+ 9+ 11= 27 – это 3 в кубе
13+15+ 17+ 19= это 4 в кубе
Демонстрируется слайд
Большой популярностью в даже в наши дни пользуются магические квадраты. Это квадраты в каждую клетку которых вписаны числа так,что сумма числа вдоль горизонтали, вертикали, и диагонали равны.
Демонстрируется слайд Учитель английского языка – Look at the screen. you can see the engraving ‘Melancholia’
by Albrecht Durer the famous German artist. In his engraving you can see a genius who suffers
from melancholia, which means depression. And Durer placed a magic square in his engraving.
Here it is
How many numbers are there in every row?-4
Yes it’s a square of 4. we can also call it 4by 4 square. In the bottom row of the square you can see the mumbers 15 and 14.
Now each student of the group will get a part of the text about magic squares. You are to read your part of the text and be ready to share the information you will learn from your part with the students of your group.
And I hope you’ll find out why Durer placed a magic square of 4 in his engraving and what the numbers 15 and 14 in the bottom row of the square mean.
(учащимся раздаются части текста о магических квадратах)
| The magic square mathematical game has existed throughout history and in many different parts of the world. Magic squares have been studied for at least three thousand years, the earliest recorded appearance dating to about 2200 BC, in China. In the 9th century, Arab astrologers used them in calculating horoscopes, and by 1300 AD, magic squares had spread to the West. Arab horoscopes гороскопы |
| Magic squares were greatly popular in West Africa. Magic squares were interwoventhroughout the culture of West Africa. The squares held particular spiritual importance and were inscribed on clothing, masks, and religious artifacts. They influenced the design and building of houses. evident очевиден interwoven переплетен throughout повсюду spiritual духовный were inscribed были начертаны artifacts. памятники материальной культуры |
| An engraving by the German artist included a magic square. In the engraving you can see a genius, who suffers from melancholia, which we call depression. The square of 4 is the square of Jupiter and it was thought to bring down the influence of the planet Jupiter. The planet Jupiter was considered beneficial, and helped to cure depression. In the bottom row of his 4 X 4 magic square you can see that Albrecht Dürer placed the numbers "15" and "14" side by side to show he date of his engraving. engraving гравюра Dürer Дюрер Jupiter Юпитер beneficial благотворный, целебный genius дух melancholia меланхолия |
Because the concept of a magic square is so easily understood, magic squares have been particularly attractive to puzzlers and amateur mathematicians. Even Benjamin Franklin was fond of magic squares, and an  magic square with some very interesting properties is attributed to him.
amateur любитель
puzzlers человек, увлекающийся головоломками
properties свойства
attributed приписываются
|
Учитель английского языка-Now students 1 2
3 
4 share the information
Now students who read the parts 1 2
3 
4 turn to each other and share your information
Thank you now students 1 2 3 4
(учащиеся по очереди пересказывают друг другу тот отрывок текста, который они прочитали, затем меняются партнерами и пересказывают им содержание своего отрывка)
And now let’s complete the sentences according to the contents of the text. Work in group
(учащиеся выполняют задание в группах, затем учитель проверяет правильность выполнения фронтально)
Complete the sentences choosing the right variant
1. Arab astrologers used magic squares
a) on clothing b) in calculating horoscopes c) in religious artifact
2. According to the text magic squares were greatly popular in
a) North America b) West Africa c) South America
3. The square of 4 is the square of….
a) Venus b) Mars c) Jupiter
and it is considered to be able to
a) to help to cure depression
b) to attract money
c) to bring good luck
4. Durer placed the numbers “15 “ and “14” in the bottom row of his magic square
| a) to show the year when he was born b) to show the date of his engraving c) without any reason | a) An 8 by 8 b) A 6 by 6 c) A16 by 16 |
magic square with some interesting properties attributed to
a) Benjamin Franklin
b) George Washington
c) Abraham Lincoln
Учитель английского языка- And now you can also try to solve such magic squares
(учащимся раздаются магические квадраты на разноцветных листах бумаги. Ученики в группе берут карточки с квадратами разного цвета и заполняют их, затем объединяются в группы по цвету квадратов и заполняют один большой квадрат. Правильность заполнения проверяют с помощью слайда)
Учитель математики- а сейчас давайте подведем итоги нашего урока при помощи синквейна. Вы знаете синквейн – это такое стихотворение в котором.
правая строка – одно слово, обычно существительное, отражающее главную идею;
вторая строка – два слова, прилагательные, описывающие основную мысль;
третья строка – три слова, глаголы, описывающие действия в рамках темы;
четвертая строка - фраза из 4 слов, показывающая отношение к теме; (вы видите у нас получилась арифметическая прогрессия)
пятая строка – слова, связанные с первым, отражающие сущность темы.
Учащиеся составляют синквейны на английском и русском языках и читают их
| Урок Необычный, увлекательный Думаем, решаем, общаемся Я умею решать задачи Интересно | Gauss Bright, clever Solved, developed, investigated He contributed so much Genius |
| Squares Magic, coloured Think, add, place I did it myself Interesting | Работа в группе Весело, увлекательно Решать, обсуждать, помогать Мне нравиться так учиться Мы вместе |
Английский язык + мировая художественная культура
«Западноевропейская художественная культура Средневековья»
Класс
(МОУ «СОШ№ 27 с углубленным изучением отдельных предметов» г.Балаково)
Авторы: Субоч Р. И., учитель русского языка и литературы,
Леонова И. В., учитель английского языка
Ход урока
1.Вступительное слово учителя МХК.
Наш урок я хочу начать с упоминания имени патриарха Всея Руси Алексия Второго, с которым недавно простился весь мир. Мы стали свидетелями того как едины были верующие разных стран и народов в проявлении уважения к человеку, посвятившему себя служению идеалам веры, добра, милосердия, терпения. Этот факт наглядно убеждает в том, что, несмотря на существующие различия в церковной и соответственно культурной практике, исходные ценности христианской религии всегда были едины. На предыдущем уроке мы говорили о художественной культуре православной традиции, а сегодня, продолжая знакомство с эпохой Средневековья, обратимся к западноевропейской художественной культуре средневекового искусства католической традиции, сформировавшей основу национальных художественных культур многих современных европейских государств, в частности Англии, поэтому мы проводим интегрированный урок МХК и английского языка. Запишем тему урока в тетради.
- Французский поэт XIX века Т.Готье писал:
В погоне за стихом, за ускользнувшим словом,
Я к замкам уходить люблю средневековым.
Мне сердце радует их сумрачная тишь,
Мне любы острый взлет их черно-сизых крыш,
Угрюмые зубцы на башнях и воротах,
Квадраты стеклышек в свинцовых переплетах.
Подъемные мосты, глубоких рвов провалы,
Крутые лестницы и сводчатые залы,
Где ветер шелестит и стонет в вышине,
О битвах и пирах рассказывает мне…
И погружен мечтой в былое, вижу вновь я
Величье рыцарства и блеск Средневековья.
Перевод А.Эфрон
Однако писатели – гуманисты XV-XVI вв. называли Средние века «темной ночью», «эпохой умственного застоя». Цель нашего урока – выяснить, справедливо ли это мнение, или все-таки прав Т.Готье отметив в стихотворении «величье рыцарства и блеск Средневековья».
Предполагаемый ответ: правы писатели-гуманисты либо они ошибаются и тогда прав Т.Готье. (Гипотеза исследования).
- В Средние века архитектура становится главным видом искусства, подчиняющим себе другие виды. В ней традиционно выделяют два стиля: романский (X-XII вв.) и готический (XIII-XV вв.). Откроем учебник на странице 149, прочитаем материал о романском искусстве (предпоследний и последний абзацы) и ответим на вопрос: какой христианский идеал существовал в романском искусстве?
- Архитектурный облик Средневековья трудно представить без феодального замка, являющегося неотъемлемой частью средневекового образа жизни. Послушаем сообщение о замке феодала и подумаем: каково же предназначение этого сооружения?
2. Сообщение ученика о замке феодала.
В это время в архитектуре получил распространение романский стиль. Романские сооружения разбросаны по всей Европе, символом этого стиля можно считать укрепленный замок феодала, который служил убежищем в период нескончаемых войн. Замок обычно возводился на вершине скалистого холма или горы, над рекой или у моря. Он окружался рвом, через который перекидывали подъемный мост, ведущий к воротам. Монолитные стены крепости увенчивались зубцами, башнями и бойницами. В центре замкового комплекса была самая крупная башня- донжон- убежище феодала.
Замок феодала – это не только жилище феодала, оборонительное сооружение, но и своеобразный центр культуры. В замке проходили рыцарские турниры, устраивались состязания певцов и музыкантов, выступали бродячие актеры.
- Каково же предназначение этого сооружения? Ответить на этот вопрос поможет и материал учебника на странице 150.
3. Учитель МХК.
В XI-XII веках у разных народов Европы сложилась письменная литература на родном языке.
Средневековый эпос разнообразен. У французов огромной популярностью пользовались поэмы, рассказывающие о событиях времен Карла Великого, в Германии результатом поэтической переработки старинных героических песен стала эпопея «Песнь о нибелунгах», среди кельтских сказаний выделяется поэма о рыцаре Парцифале (Парсифале), отправившегося на поиски Святого Грааля – чаши с кровью распятого Спасителя, в Англии - баллады о Робин Гуде.
Кто же такой Робин Гуд? Слово учителю английского языка.
4. Учитель английского языка: Сообщение о Робин Гуде на англ.языке.
5.Учитель МХК: Какие черты характера Робина определили его исключительность и позволили ему стать лидером?
6.Учитель англ.яз: Прочитаем балладу «Робин Гуд и король».
7.Учитель МХК: Каким предстает перед нами Робин Гуд как герой народной баллады?
При всей непохожести сюжетов в европейском эпосе разных народов много общего. В нем превозносились смелость, преданность долгу, бескорыстное служение родине и сюзерену, способность отдать жизнь во имя идеи. Причудливо переплетаются реальные исторические события, картины рыцарского и придворного быта, фантастические образы, почерпнутые из народных преданий.
Приоритетными стали темы, воспевающие высоту духовного подвига и нравственные идеалы, отвечающие христианским заповедям. Не случайно именно в этот период и появились рыцари. А как возникло рыцарство, например, в Англии?
8. Учитель англ.яз: Историческая справка об английских рыцарях (синхронный перевод).
9.Учитель МХК: Рыцарь, закованный в латы, тяжелым ударом разящий врага, стал героем письменной литературы. Английский писатель Средневековья Томас Мелори обратился именно к рыцарской теме не случайно. Познакомимся с его творчеством.
10. Сообщение на русском языке о Томасе Мелори.
11. Слово учителю англ.яз., проводится аудирование.
12. Учитель МХК: Царицей словесности стала поэзия, в которой рыцари были далеко не единственными ее героями. Прекрасной Даме, которой поклонялся рыцарь, он посвящал свои стихи и песни, воспевал красоту и добродетели своей избранницы (обычно знатной дамы или даже королевы). Ради возлюбленной рыцарь совершал свои подвиги, с ее именем на устах сражался он на военных турнирах. Предлагаем вашему вниманию фрагмент фильма, в котором воссоздана атмосфера рыцарского турнира. Это современное видение рыцарского поединка, колорит эпохи передан и благодаря воспроизведению места действия, одежды рыцарей, их снаряжения и экипировки.
Послушаем сообщение о любовной рыцарской поэзии, в учебнике этот материал вы найдете на страницах158-159.
13. Сообщение о любовной рыцарской поэзии.
С ростом городов и развитием светской замковой культуры все большее значение приобретает любовная рыцарская поэзия, получившая название куртуазной (что означает придворной). В ней воспевалась Прекрасная Дама, которой поклонялся рыцарь.
Поразительно, что изысканная куртуазная поэзия зародилась в среде рыцарей, еще совсем недавно невежественных вояк, круг интересов которых не выходил за пределы быта, оружия, крестовых походов. Превращению грубых крестоносцев в придворных аристократов способствовала новая система воспитания: молодых людей стали обучать не только военному делу, но и красивой и правильной речи, стихотворному искусству, танцам, игре на музыкальных инструментах, обходительным манерам и правилам хорошего тона. Все это и составило куртуазность, сложившуюся в XI веке.
14. Учитель МХК.
Итак, любовная рыцарская поэзия, героиней которой стала Прекрасная Дама, привлекала к себе поэтов и в более поздние века. Так, например, Альфред лорд Теннисон, английский поэт, живший в 19 веке, использовал этот средневековый образ в своем творчестве. Слово учителю английского языка.
15. Презентация о Теннисоне на русском языке, рассказ на английском языке.
16.Учитель англ.яз.
Представляем вашему вниманию стихотворение Теннисона о леди Вивьен.
17. Чтение стихотворения «Леди Вивьен».
18. Учитель МХК: Что вы можете сказать о героине этого стихотворения?
19. Предполагаемый ответ ученицы.
Понятно, что героиня названа в заглавии стихотворения, однако, наряду с этим мы можем сказать, что подлинной героиней является куртуазная любовь – трепетное обожание, возвышенное, тайное и лишенное взаимности чувство. В любовном томлении по недосягаемому идеалу поэт находит особую прелесть, очарование, умножающее полноту жизни и дарующую вдохновение.
Подведение итогов.
1.Учитель МХК: Наряду с художественной культурой православной Руси, в католическом православном мире набирала силу вторая ветвь христианской традиции. Мы познакомились с светским искусством европейского Средневековья, в результате мы должны сейчас согласиться с определением или опровергнуть мнение писателей- гуманистов, назвавших Средние века «эпохой умственного застоя», «темной ночью» или выразить свою солидарность с точкой зрения Т.Готье о «о величье рыцарства и блеске Средневековья».
Предполагаемый ответ: Нет, произведения искусства, к которым мы сегодня обратились, убедили нас в том, что средневековая культура внесла свой вклад в развитие мировой художественной культуры и заняла в ней почетное место. Художественная культура Средних веков в большей степени подчеркивала духовную сущность человека, его суровый аскетический облик, это важнейший этап художественного развития человечества, заложивший фундамент современной цивилизации.
2.Учитель англ.яз: Сегодняшнее обращение к английскому Средневековью углубило и расширило наше представление о стране, о литературе и в целом о культуре Англии. Причем звучала хорошая, правильная речь не только на русском языке, но и на языке оригинала. Думаю, что все ученики, принявшие участие в уроке заслуживают только высоких оценок.
Домашнее задание.
Предлагаем творческое задание: попробовать свои силы в качестве переводчика стихотворения Альфреда Теннисона «Леди Вивьен», а также ответить на вопрос: почему поэт 19 века обратился в своем творчестве к эпохе Средневековья.
Античный театр 10 класс
Автор: Лабазова В. Н., преподаватель английского языка
Ход урока
|
|
|
