 |
Исследование и решение произвольной системы линейных уравнений
|
|
|
|
Т. В. Тарбокова
Сборник справочных материалов
По курсу высшей математики

Томск 2006
УДК 517
Т 19
Тарбокова Т. В.
Т 19 Сборник справочных материалов по курсу высшей математики: Учебное пособие / Т.В. Тарбокова. – Томск: Изд-во ТПУ, 2006. – 79 с.
Сборник справочных материалов содержит сведения по всем разделам курса высшей математики, изучаемого в вузе, и способствует развитию творческих способностей, математического мышления студентов, активизации их познавательной деятельности и самостоятельной работы. Включает теоретические сведения, оформленные в виде структурно-логических схем, алгоритмов решения задач, крупноблочного представления материала. Для студентов всех специальностей вузов.
УДК 517
Рекомендовано к печати Редакционно-издательским
советом Томского политехнического университета
Рецензенты
Кандидат физико-математических наук,
профессор, заведующий кафедрой математики ТУСУР
Л.И. Магазинников
Кандидат физико-математических наук,
доцент кафедры математического анализа ТГУ
Л.С. Копанева
© Оформление. Издательство ТПУ, 2006
© Томский политехнический университет, 2006
 |
МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ, СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Метод окаймляющих миноров нахождения ранга матрицы

| Определение минора. | Минором  порядка k матрицы А называется любой определитель k -го порядка этой матрицы, составленный из элементов, стоящих на пересечении любых её «к» столбцов и любых её «к» строк порядка k матрицы А называется любой определитель k -го порядка этой матрицы, составленный из элементов, стоящих на пересечении любых её «к» столбцов и любых её «к» строк

|
| |||||||
| |||||||
| |||||||
| |||||||
|
|
|
|
 |

| Определение ранга матрицы. | Рангом r матрицы А называется наибольший порядок r минора этой матрицы, отличного от нуля:
  (существует минор порядка r, не равный нулю, а все миноры более высоких порядков равны нулю или не существуют).
(существует минор порядка r, не равный нулю, а все миноры более высоких порядков равны нулю или не существуют).
|
Алгоритм приведения матрицы к ступенчатому виду
Элементарными преобразованиями
Условимся называть рабочей строку, которая не изменяется на проводимом этапе элементарных преобразований (перестановке строк; умножении строки на число и сложении с соответствующими элементами другой строки; вычеркиванием всех пропорциональных строк, кроме одной из них).
Рабочая строка первая. Получим нули в первом столбце на местах всех элементов первого столбца за исключением элемента в первой строке а 11. Для этого умножим все элементы первой строки на такие числа, чтобы при сложении с элементами первого столбца остальных строк получить нули в первом столбце, за исключением элемента первой строки а 11.
Если в системе, которую Вы решаете, коэффициент при х 1 в первом уравнении не равен единице, поменяйте местами строки, записав первой ту, в которой коэффициент при неизвестном х 1 равен единице.
Если при неизвестном х 1 во всех уравнениях коэффициенты отличны от единицы, можно:
1) умножить первую строку расширенной матрицы системы на число, противоположное тому, на месте которого Вы хотите получить ноль; а строку, в которой хотите получить ноль, умножьте на коэффициент при х 1 в первой строке;
2) сложите соответствующие элементы умноженной первой строки и умноженной другой строки.






 (3) ~
(3) ~  ~
~
Далее нужно получить нули во втором столбце ниже главной диагонали.
Рабочая строка вторая. Получаем нули во втором столбце ниже элемента а22 .
Умножим третью строку на (–14) и сложим с соответствующими элементами второй строки. (Или можно было поменять местами вторую и третью строки, чтобы на главной диагонали оказалась единица (см. (*))).
|
|
|




 ~
~  ;
;



 (*)
(*) 
Замечание. Полученная в скобках матрица (*) также эквивалентна исходной матрице  , то есть имеет тот же ранг, а системы уравнений, соответствующие этим матрицам, имеют одинаковые решения.
, то есть имеет тот же ранг, а системы уравнений, соответствующие этим матрицам, имеют одинаковые решения.
Вычисление определителей
Правило треугольников для вычисления определителей третьего порядка:
|

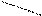














+ –
Таблица Саррюса для вычисления определителей третьего порядка:
1 2 3 1 2 ─ столбцы.



















 |  | ||||||
 | |||||||
 | |||||||
Правило разложения определителя по элементам какой-либо его строки или столбца с использованием понятия минора и алгебраического дополнения
Определение
минора  элемента
элемента  определителя
n -го порядка.
определителя
n -го порядка.
| Минором 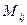 элемента элемента  определителя n- го порядка называется
определитель (n– 1 )- го порядка, полученный из данного определителя вычеркиванием элементов i- й строки и j- го столбца. определителя n- го порядка называется
определитель (n– 1 )- го порядка, полученный из данного определителя вычеркиванием элементов i- й строки и j- го столбца.
|
Определение алгебраического дополнения  элемента элемента  определителя n -го порядка. определителя n -го порядка.
| Алгебраическим дополнением  элемента элемента  называется минор этого элемента, умноженный на называется минор этого элемента, умноженный на  : :

|
В соответствии со свойствами определитель порядка n может быть представлен в виде разложения этого определителя по элементам i- й строки:

 .
.
То есть определитель квадратной матрицы А порядка n равен сумме произведений элементов какой-либо i-й его строки на алгебраические дополнения этих элементов.
Аналогичным образом можно разложить этот же определитель по элементам любого его столбца.
Так для определителя третьего порядка формула разложения определителя по элементам второго столбца получится следующей:

 =
=
=  .
.
Определители второго порядка получаются, если вычеркнуть в определителе третьего порядка второй столбец и, соответственно, первую, потом вторую, потом третью строки.
Действия над матрицами
| Определение суммы двух матриц. | Суммой двух матриц  и и  с одинаковым количеством m строк и с одинаковым количеством m строк и  столбцов называется матрица столбцов называется матрица  , элементы которой равны сумме соответствующих элементов слагаемых матриц: , элементы которой равны сумме соответствующих элементов слагаемых матриц:  . Обозначение: . Обозначение: 
|

 =
=  =
=  .
.
|
|
|
| Определение произведения матрицы на число. | Произведением матрицы  на число на число  называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы  на число на число  : :
 . .
|
Например.  .
.
| Определение произведения матрицы-строки на матрицу-столбец. | Произведением матрицы-строки, имеющей  столбцов, на матрицу-столбец, имеющий столько же строк, называется матрица, состоящая из одного элемента, который равен сумме произведений соответствующих элементов перемножаемых матриц: столбцов, на матрицу-столбец, имеющий столько же строк, называется матрица, состоящая из одного элемента, который равен сумме произведений соответствующих элементов перемножаемых матриц:  , ,
|
|
 .
.  .
.
| Условие существования произведения двух матриц. | Произведение матриц  существует только в тех случаях, когда число столбцов матрицы существует только в тех случаях, когда число столбцов матрицы  равно числу строк матрицы равно числу строк матрицы  , то есть , то есть  . При этом матрица-произведение имеет число строк матрицы . При этом матрица-произведение имеет число строк матрицы  и число столбцов матрицы и число столбцов матрицы  . .
|
| Определение перестановочных матриц. | Квадратные матрицы, произведение которых коммутативно:  , называются перестановочными. , называются перестановочными.
|
| Определение произведения матриц. | Произведением матрицы  , имеющей , имеющей  строк и строк и  столбцов, на матрицу столбцов, на матрицу  , имеющую , имеющую  строк и строк и 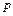 столбцов, называется матрица столбцов, называется матрица  , имеющая , имеющая  строк и строк и 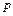 столбцов, у которой элемент столбцов, у которой элемент  равен сумме произведений элементов равен сумме произведений элементов  -й строки матрицы -й строки матрицы  и и  -го столбца матрицы -го столбца матрицы  , ,
|
то есть  .
.
Произведение матриц обозначается  .
.
Замечание. Правило умножения матриц можно легко запомнить, если сформулировать его в следующем виде: элемент  матрицы
матрицы  , стоящий на пересечении
, стоящий на пересечении  -й строки и
-й строки и  -го столбца, есть скалярное произведение
-го столбца, есть скалярное произведение  -й вектор – строки матрицы
-й вектор – строки матрицы  и
и  -го вектор – столбца матрицы
-го вектор – столбца матрицы  .
.
 =
=  .
.
| Определение единичной матрицы. | Квадратная матрица, на главной диагонали которой все элементы равны единице, а все остальные элементы нули, называется единичной матрицей и обозначается буквой  . .
|
| Определение обратной матрицы. | Обратной для матрицы  называется такая матрица называется такая матрица  , что их произведение равно единичной матрице: , что их произведение равно единичной матрице: 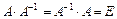 . .
|
| Теорема существования обратной матрицы. | Для любой квадратной матрицы  , определитель которой не равен нулю , определитель которой не равен нулю  , существует единственная обратная матрица , существует единственная обратная матрица  . .
|
|
|
|
| Определение невырожденной и вырожденной матриц. | Матрица, определитель которой не равен нулю, называется невырожденной. Матрица, определитель которой равен нулю, называется вырожденной. |
Чтобы найти обратную для  матрицу
матрицу  , можно действовать следующим образом:
, можно действовать следующим образом:
1. Вычислить определитель матрицы 
 .
.
Если  , то матрица
, то матрица  не имеет обратной
не имеет обратной  .
.
2. Составить союзную матрицу из алгебраических дополнений соответствующих элементов матрицы  :
:  .
.
3. Транспонировать союзную матрицу, то есть заменить строки на столбцы с такими же номерами:  .
.
4. Разделить транспонированную союзную матрицу на определитель матрицы  :
:  .
.
Например.
1.  . 2.
. 2.  . Вспомните, что
. Вспомните, что  .
.
3.  4.
4.  .
.
Проверим, правильно ли найдена обратная матрица:
 =
=  =
=  .
.
| Определение линейной зависимости (независимости) системы | Система строк (столбцов, векторов, решений)  называется линейно зависимой, если линейная комбинация называется линейно зависимой, если линейная комбинация  , когда не все коэффициенты линейной комбинации , когда не все коэффициенты линейной комбинации  ─ нули,
и называется линейно независимой, если линейная комбинация ─ нули,
и называется линейно независимой, если линейная комбинация  , когда все коэффициенты линейной комбинации , когда все коэффициенты линейной комбинации  ─ нули. ─ нули.
|
Исследование и решение произвольной системы линейных уравнений
| Определение базисного минора и базисных неизвестных. | Любой, не равный нулю минор, имеющий порядок ранга основной и расширенной матриц системы, называется базиснымминором, а неизвестные, коэффициенты при которых вошли в базисный минор – базисными неизвестными. |
| Определение свободных неизвестных. | Неизвестные, коэффициенты при которых не вошли в базисный минор, называются свободными. |
| Определение СОЛУ. | Система линейных уравнений называется однородной, если свободные члены во всех уравнениях этой системы равны нулю. AX = 0 – матричная запись СОЛУ. |
Система однородных линейных уравнений всегда совместна, поскольку имеет так называемое тривиальное решение, когда все неизвестные равны нулю: X = 0,  . Ранги основной и расширенной матриц системы однородных линейных уравнений всегда равны, так как вычеркивание нулевого столбца свободных членов не изменяет ранга матрицы, поэтому по теореме Кронекера-Капели СОЛУ всегда совместна.
. Ранги основной и расширенной матриц системы однородных линейных уравнений всегда равны, так как вычеркивание нулевого столбца свободных членов не изменяет ранга матрицы, поэтому по теореме Кронекера-Капели СОЛУ всегда совместна.
| Определение ФСЧР СОЛУ. | Фундаментальной системой частных решений системы однородных линейных уравнений называется система линейно независимых частных решений, число решений в которой равно числу свободных неизвестных системы. |
Если n – число неизвестных системы, r – её ранг, то ФСЧР СОЛУ должна содержать k = n – r линейно независимых частных решений.
Фундаментальную систему частных решений получают обычно, последовательно приравнивая свободные неизвестные элементам строк единичной матрицы  порядка
порядка  .
.
|
|
|
Замечание. ФСЧР СОЛУ можно получить также, приравнивая свободные неизвестные элементам строк произвольной квадратной матрицы А порядка k = n – r, если  .
.
|
|
|


