Дифференциальное исчисление функции нескольких переменных (фнп)

Определениечастной производной. Если в точке М (х, у) существует предел отношения частного приращения ФНП z = f (x,y) по одному из ее аргументов к приращению этого аргумента при стремлении приращения аргумента к нулю, то этот предел называется частной производной ФНП по этому аргументу в точке М (х, у): ; . Правило.Чтобы найти частную производную ФНП по одному из ее аргументов, надо все остальные аргументы ФНП считать постоянными и применять правила дифференцирования и таблицу производных функции одного аргумента, по которому берется частная производная	Градиент функции : Градиент функции в точке характеризует направление и величину максимальной скорости возрастания этой функции в данной точке.	Экстремум функции двух переменных 1. Необходимое условие существования экстремума. Если функция f (x,y) имеет в точке М0 (х0,у0) экстремум и имеет в точке М0 частные производные первого порядка, то в этой точке частные производные первого порядка равны нулю, т. е. . 2. Достаточные условия существования экстремума. Пусть . Тогда а) если D> 0, то в точке М0 функция имеет экстремум, причем при – локальный максимум, при – локальный минимум; б) если D<0, то в точке М0 экстремума нет; в) если D=0, то требуются дополнительные исследования.
Производная по направлению Вектор направления ; Орт направления: ; Производная по направлению равна скалярному произведению градиента на орт направления:
Производные сложных функций ; u, v – промежуточные аргументы, x,.y – основные аргументы.	Уравнение касательной плоскостик поверхности F (x,y,z) =0 в точке М0 (х0,у0,z0) Скалярное произведение , или	Алгоритм нахождения наибольшего и наименьшего значений функции двух переменных в ограниченной замкнутой области 1. Найти точки, принадлежащие области, в которых частные производные первого порядка равны нулю или не существуют. Вычислить значения функции в этих точках. 2. Заменить одну из независимых переменных из уравнения границы области и найти наибольшее и наименьшее значения получившейся функции одного аргумента на отрезке изменения этого аргумента: вычислить значения функции в критических точках первого порядка и на концах отрезка. 3. Из всех полученных значений функции выбрать наибольшее и наименьшее.
Производные неявно заданных функций F (x,y,z) = 0, Û z = f (x,y). .	Уравнение нормалик поверхности F (x,y,z) =0 в точке М0 (х0,у0,z0)   векторное произведение 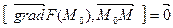, или
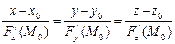
Полный дифференциал ФНП . Полный дифференциал ФНП равен сумме ее частных дифференциалов: .

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Интегралы от скалярной функции

	Определенный	Двойной	Тройной	Криволинейный I рода	Поверхностный I рода
W	M Î R 1 W:{" x Î[ a,b ]} отрезок оси О Х	M Î R 2 W-область D в плоскости X O Y S-площадь D	M Î R 3 W – область трехмерного пространства. V -некоторый объем.	M Î R 3 W-дуга кривой l в R 3	M Î R 3 W-часть поверхности s в R 3
D W М i	DW=Dx M i=xiÎD x i	DW=D S =D x D y M i(xi,hi)Î∆ S i	DW=DV=DxDyDz M i(xi,hi,zi)Î∆ Vi	DW=D l- элемент дуги кривой M i(xi,hi,zi)ÎD li	DW=Ds-элемент поверхности M i(xi,hi,zi)ÎDsi
Определение, обозначение инт-ла
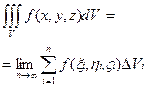
Геометрический и физический смысл.	S – площадь криволинейной трапеции	Уравнение поверхности: z = f(x,y) D Mi(xi,hi)	f (x,y,z) – плотность в т. М тела V m телаV	f (x,y,z) – плотность в т. М кривой l = m кривой l	s f (x,y,z) – плотность в т. М поверхности s =mповерхности f (x,y,z)=1Þ