|
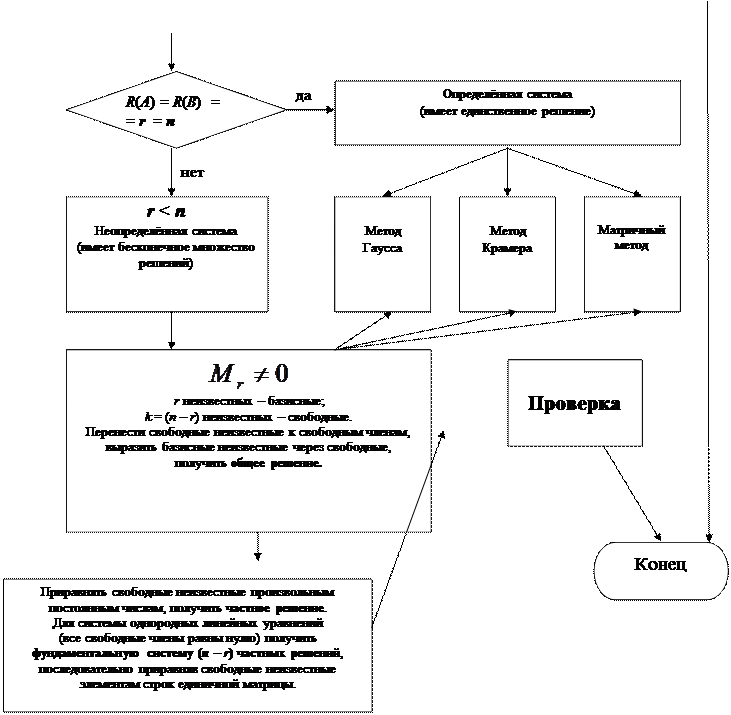
Блок-схема исследования и решения произвольной системы линейных уравнений
|
|
|
|
 R (А) – ранг основной матрицы системы;
R (А) – ранг основной матрицы системы;
 R (В) – ранг расширенной матрицы системы;
R (В) – ранг расширенной матрицы системы;
М r – базисный минор;
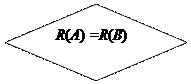
|
| |||||||||
 | |||||||||
 | |||||||||
 |  | ||||||||

ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Координаты вектора  находят, вычитая из координат точки
находят, вычитая из координат точки 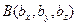 , являющейся концом вектора, соответствующие координаты точки
, являющейся концом вектора, соответствующие координаты точки  , являющейся началом вектора.
, являющейся началом вектора.
 =
=  .
.
Косинус угла между векторами  и
и  равен отношению скалярного произведения этих векторов к произведению длин этих векторов:
равен отношению скалярного произведения этих векторов к произведению длин этих векторов:  .
.
Скалярное произведение двух векторов в ортонормированном (декартовом) базисе равно сумме произведений одноименных координат этих векторов: если  , то
, то  .
.
Длина вектора 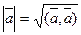 в ортонормированном базисе равна корню квадратному из суммы квадратов координат этого вектора. Например, если
в ортонормированном базисе равна корню квадратному из суммы квадратов координат этого вектора. Например, если  то
то 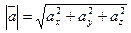 .
. 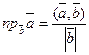 – проекция вектора
– проекция вектора  на вектор
на вектор  .
.
В ортонормированном базисе векторное произведение находят, раскладывая определитель, в первой строке которого – орты  декартовой системы координат, во второй строке – координаты левого из перемножаемых векторов, а в третьей строке – координаты правого из перемножаемых векторов.
декартовой системы координат, во второй строке – координаты левого из перемножаемых векторов, а в третьей строке – координаты правого из перемножаемых векторов.
 Например,
Например, 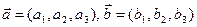 , тогда векторное произведение этих векторов в декартовой системе координат можно найти так: Свойства векторного произведения
, тогда векторное произведение этих векторов в декартовой системе координат можно найти так: Свойства векторного произведения
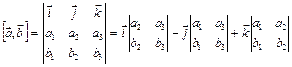 .
. 
| Геометрический смысл векторного произведения. | Модульвекторного произведениячисленно равенплощади параллелограмма,построенного на перемножаемых векторах как на двух смежных сторонах. Обычно векторы приводят к общему началу. Половина модулявекторного произведениячисленно равнаплощади треугольника,построенного на перемножаемых векторах как на двух смежных сторонах этого треугольника. Обычно векторы приводят к общему началу. |
|
|
|
| Определение и условие компланарности векторов. | Векторы, лежащие в одной или параллельных плоскостях, называются компланарными. Смешанноепроизведение ненулевых компланарныхвекторов равно нулю. |
Смешанное произведение трех векторов получают, умножая векторное произведение двух векторов на третий вектор скалярно.
В ортонормированном базисе смешанное произведение равно определителю, строками или столбцами которого являются координаты перемножаемых векторов. Обычно первой строкой определителя записывают координаты первого вектора, второй строкой – координаты второго вектора, а третьей строкой – координаты третьего вектора, если считать векторы слева направо.
Полезно помнить такие свойства смешанного произведения: 1) при перестановке двух любых соседних векторов смешанное произведение меняет знак на противоположный; 2) при циклической перестановке (последний вектор ставится впереди первого) смешанное произведение не изменяется, поскольку при этом два раза переставляются соседние векторы.
| Геометрический смысл смешанного произведения. Деление отрезка в отношении λ. | Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах как на ребрах. Обычно векторы приводят к общему началу. Объём пирамиды, построенной на векторах  , , 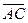 и и 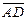 , равен одной шестой объёма параллелепипеда, построенного на этих же векторах как на ребрах , равен одной шестой объёма параллелепипеда, построенного на этих же векторах как на ребрах
 : :  . .
|
ГЕОМЕТРИЯ ПРЯМЫХ И ПЛОСКОСТЕЙ В ТАБЛИЦАХ
Уравнения плоскости Р в трехмерном пространстве R 3 и уравнения прямой L
в двухмерном пространстве R 2
Таблица 1
| Уравнения плоскости Р в R 3 в координатной форме | Векторная форма уравнений P, L в R 3 и R 2 | Уравнения прямой L в R 2 в координатной форме | ||||||||
| I R 3 Уравнения P и L, проходящих через данную точку М 1 R 2I перпендикулярно данному вектору N | ||||||||||
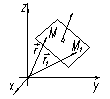 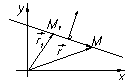 N =(A, B, C)
r = (x,y,z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1 ,z 1)Î P
" M (x,y,z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0 N =(A, B, C)
r = (x,y,z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1 ,z 1)Î P
" M (x,y,z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0
| r-r 1 = M 1 M M 1 M ^ N (P) M 1 M ^ N (L) (r-r 1, N) = 0 (M 1 M, N) = 0 Условие ортогональности векторов | N = (A,B) r = (x,y) r 1 = (x 1, y 1) M (x 1, y 1) Î L " M (x,y) Î L A (x-x 1)+ B (y-y 1) = 0 | ||||||||
| II R 3 Общие уравнения R 2 II | ||||||||||
| Ax + By + Cz + D = 0 D = -Ax 1 - By 1 - Cz 1 | (r,N) + D = 0 D = – (r1, N) | Ax + By +D = 0 D = -Ax 1 -By 1 | ||||||||
| III R3 Через n фиксированных точек M R2 III | ||||||||||
| n = 3 | n = 2 | |||||||||
M 1(x 1 ,y 1, z, 1)Î P, М 1 М Î Р
M 2(x 2, y 2, z 2)Î P, М 2 М 1Î Р
M 3(x 3, y 3, z 3)Î P, М 3 М 1Î Р
" M (x,y,z)Î P  

| M 1 Î P, L M 2 Î P, L " M Î P, L M 3 Î P | M 1(x1,y1) Î L,
M 2(x2,y2) Î L
" M (x,y) Î L
М 1 М çç М 2 М 1
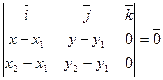

| ||||||||

| (M 1 M, M 1 M 2, M 1 M 3)=0 Условие компланарности векторов | [ M 1 M, M 1 M 2] = 0 Условие коллинеарности векторов | ||||||||


| A =y 2 -y 1; B = – (x 2 -x 1), Û A (x-x 1) + B (y-y 1) = 0 (1. I.) | |||||||||
| IV R 3 Уравнения в отрезках R 2 IV | ||||||||||
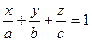 y= 0, z= 0 Þ x=a
x= 0, z= 0 Þ y=b
x= 0, y= 0 Þ z=c
y= 0, z= 0 Þ x=a
x= 0, z= 0 Þ y=b
x= 0, y= 0 Þ z=c
| r = xi+yj+zk t = i/a +j/b +k/c (r,t) = 1 t = (1 /a, 1 /b, 1 /c) ç r ç cos (r,t) = 1/ ç t ç |

 y= 0 Þ x=a
x= 0 Þ y=b y= 0 Þ x=a
x= 0 Þ y=b
| ||||||||
|
|
|
Уравнения прямой L в трехмерном пространстве R 3 и в двухмерном пространстве R 2
Таблица 2
| Уравнения прямой L в R 3 в координатной форме | Векторная форма уравнений прямой L в R 2 и R 3 | Уравнения прямой L в R 2 в координатной форме | ||||
| I Канонические уравнения прямой L I | ||||||
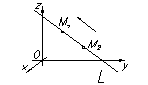  l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L
 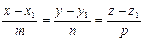
| r-r 1= M 1 M çç l r 2- r 1= M 1 M 2 çç l [ r-r 1, l ]=0 [ M 1 M, l ]=0 | l =(m,n)
l =(m,n) çç L
M 1(x 1, y 1)Î L
M 2(x 2, y 2)Î L
" M (x, y)Î L
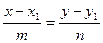
| ||||
| II Параметрические уравнения прямой L II | ||||||
 " t Î R 1 " t Î R 1
 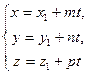

| r-r 1 çç l, " t Î R 1 M 1 M çç l r-r 1= M 1 M = tl r=r 1+ tl [ M 1 M, tl ]=0 |
 " t Î R 1 " t Î R 1
  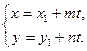
| ||||
| III Уравнения прямой L, проходящей через две данные точки M 1 и M 2 III | ||||||
l çç L, l=(m,n,p), lt = M 1 M 2
m=x 2– x 1, n=y 2– y 1, p=z 2– z 1
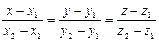
| M 1 M çç M 1 M 2 çç l M 1Î L, M 2Î L, " M Î L [ M 1 M, M 1 M 2]=0 |
l çç L, l =(m,n), tl = M 1 M 2
m=x 2– x 1, n = y 2-– y 1
.


| ||||
| IV Общие уравнения прямой L в R 3 (P 1Ç P 2) | Уравнение прямой L с угловым коэффициентом k в R 2 V | |||||
 N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0. N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0.
|
A x+ B y+ D =0, B ¹0
ß

 y = kx + b y = kx + b 
 a³0 a³0
| |||||
таблица 2 а (продолжение таблицы 2)
| Связь между уравнениями прямой L в R 3 | Связь между уравнениями прямой L в R 2 |
Общие(2.IV)
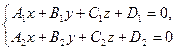
 Þ z0=0 Þ z0=0
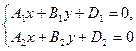 Þ M 0(x 0, y 0,0)Î L
или Þ M 0(x 0, y 0,0)Î L
или 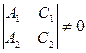 Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или  Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p) Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p)
 – канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß – канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß
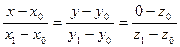 – через две
точки M 0Î L, M 1Î L (2.III) – через две
точки M 0Î L, M 1Î L (2.III)
 – общие(2.IV) – общие(2.IV)
| С угловым коэффициентом: (2.V)
y = kx+b  ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.
ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.

 через точки M 1Î L и M 2Î L
(1. III) (2.III) через точки M 1Î L и M 2Î L
(1. III) (2.III)
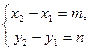 Þ Þ 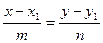 – канонические(2.I)
ß
ì n (x-x 1)= m (y-y1)
í n (x-x 1)- m (y-y 1)=0,
î n = A; –m = B;
A (x-x 1)+ B (y-y 1)=0 M 1(x 1, y 1)Î L
N =(A, B)^ L (1.I)
ß
- Ax 1– B y1= D
Ax + By + D =0 – общее(1.II)
– канонические(2.I)
ß
ì n (x-x 1)= m (y-y1)
í n (x-x 1)- m (y-y 1)=0,
î n = A; –m = B;
A (x-x 1)+ B (y-y 1)=0 M 1(x 1, y 1)Î L
N =(A, B)^ L (1.I)
ß
- Ax 1– B y1= D
Ax + By + D =0 – общее(1.II)
|
Взаимное расположение плоскостей P в трёхмерном пространстве R 3
и прямых L в двухмерном пространстве R2
ТАБЛИЦА 3
| I Обозначения, принятые в таблице 2, {P1,P2} в R3 | I | Обозначения, принятые в I таблице 2, {L1,L2} в R2 | |||
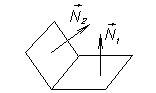 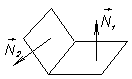  N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)
N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)
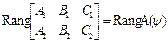

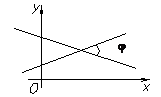
| R3 cos j =  N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2
N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2
N 1 =(A 1, B 1) N 2 =(A 2, B 2)
| a)  N1=(A1,B1);N2=(A2,B2)
N1=(A1,B1);N2=(A2,B2)

 б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j =
б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j = 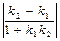 ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) =
ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) = 
| |||
| II Признаки взаимного расположения плоскостей {P1, P2} и прямых {L1, L2} II | |||||
| плоскости { Р 1, Р 2} в R n; n =3 | Как расположены P и L | Прямые { L 1, L 2} в R n; n =2 | |||
P 1 Ç P 2 (пересекаются)
cos j=  ¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y) ¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y)
|   N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
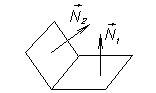 cos j ≠ ± 1 cos j ≠ ± 1
| L 1Ç L 2 (пересекаются)
a) 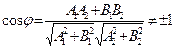 L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j=
L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j=  ¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c) ¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c)
| |||
P 1ïï P 2 (параллельны)
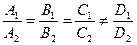 cos j = ±1
cos j = ±1
|  N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
| L 1ïï L 2 (параллельны)
а)  cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
| |||
P 1º P 2 (совпадают)
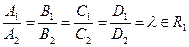 cosj = ±1
cosj = ±1
|  N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
| L 1º L 2 (совпадают)
а) 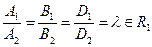 cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
|
Расстояния d(P 1, P 2) между плоскостями P 1 и P 2 и d (L 1, L 2) между прямыми
|
|
|
L 1 и L 2 в R 3, пересечение { P Ç L } плоскости P и прямой L в R 3
ТАБЛИЦА 4
| I P 1 || P 2, L 1 || L 2 в R 3 координатная форма | P 1 || P 2, L 1 || L 2,  векторная форма
векторная форма
| L 1 || L 2 в R 2II координатная форма | |
 Ü
Ü
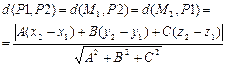
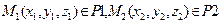
| 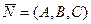 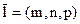
  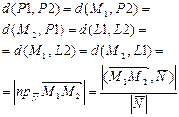
| 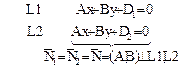 Þ
Þ
 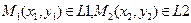
| |
 
|  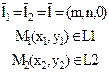
| ||
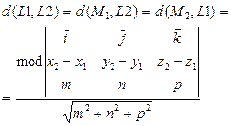 Ü Ü
|  h – высота треугольника h – высота треугольника
| Þ 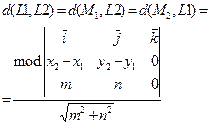
| |
| III Прямые L 1 и L 2 скрещиваются в R 3 P 1 || P 2 (L 1Ì P 1, L 2Ì P 2) | Прямая L и плоскость P пересекаются в R 3 IV { P Ç L }= M 1 | ||

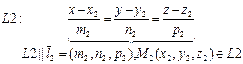
 (d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота (d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота
| 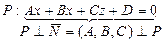
 M 0(x 0, y 0, z 0) Î L
M 0(x 0, y 0, z 0) Î L
  sin j = 0 Û L ^ P, l ïï N
sin j = 0 Û L ^ P, l ïï N
| ||
ТАБЛИЦА 4а (продолжение таблицы 4)
| VI Векторная запись условий ортогональности (P ^ L), коллинеарности (P || L) плоскости P и прямой L в R 3, пересечения P и L (P Ç L). | { P Ç L }= M 1(x 1, y 1, z 1) – координаты точкиV пересечения плоскости P и прямой L в R 3 | |||
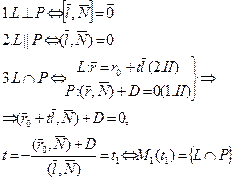
|   (2.II) Þ (2.II) Þ 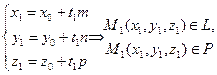
|
к -мерная плоскость Р к в точечно-векторном евклидовом n -мерном пространстве R n
ТАБЛИЦА 5
| к = n – r, Rang A = r | ||||||||||||||
AX = B

| 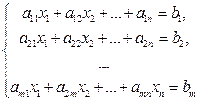
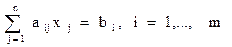
| |||||||||||||
| Система m линейных уравнений с n неизвестными | ||||||||||||||
| r = 1 гиперплоскость к = n –1 | к = 1 прямая в R r+1 n – r = 1 | к-мерная плоскость Р к0 в R n, проходящая через начало координат В =0 (СОЛУ) – система однородных линейных уравнений | Общее решение произвольной системы линейных уравнений В ¹0 (ОРСЛУ) | |||||||||||
| матричная форма | координатная форма | матричная форма | координатная форма | |||||||||||
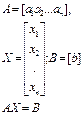
|

|
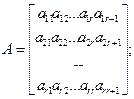
| 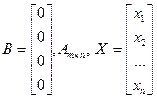
|
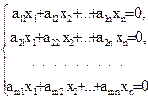
|

| |||||||||
| Плоскость в R3 n =3 | ||||||||||||||

|  Уравнение плоскости в отрезках;
Уравнение плоскости в отрезках;
|  Rang A = r = n –1
n = r + 1
AX=B
Rang A = r = n –1
n = r + 1
AX=B
| AX =0 rang A=r, x1,x2,..,xr – базисные неизвестные. Число базисных неизвестных равно r. | xr+1, xr+2,..,xn – свободные неизвестные Число свободных неизвестных равно k=n – r | Отбросить строки, не вошедшие в базисный минор, перенести свободные неизвестные в правые части уравнений, а дальше следует применить метод Гаусса, Крамера или матричный. | |||||||||
| Прямая в R 3 n =3, r =2, к =1 | Фундаментальная система частных решений СОЛУ (ФСЧР) | Частное решение произвольной СЛУ (ЧРСЛУ) | |||||
форма | координатная форма | Свободным неизвестным придать последовательно значения строк единичной матрицы Е | xr+1 = xr+2 =...= xn = 0 | ||||

|
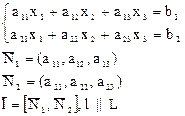
|  АХ 1 = 0 АХ 2 = 0 АХ к = 0, k=n–r.
АХ 1 = 0 АХ 2 = 0 АХ к = 0, k=n–r.
|  АС=В
АС=В
| ||||
| Прямая в R 2 n = 2, r = 1, k = 1 | Общее решение системы однородных линейных уравнений АХ 0=0 | О. Р. произвольной системы | |||||
| матричная форма | координатная форма | матричная форма | координатная форма | линейных уравнений (ОРСЛУ) АХ=В | |||
 АХ=В АХ=В
|  Уравнение прямых в отрезках
Уравнение прямых в отрезках
| 
| 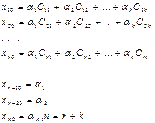
|  AX=A (X0+C)=
= AX 0+ AC= O+ B=B
AX=A (X0+C)=
= AX 0+ AC= O+ B=B
| |||
 Прямая в Rn=Rr + 1 n = r+ 1, k = 1 Прямая в Rn=Rr + 1 n = r+ 1, k = 1
| |||||||
| координатная форма | матричная форма | ||||||
 параметрические уравнения,
a 1 – параметр, свободная неизвестная параметрические уравнения,
a 1 – параметр, свободная неизвестная
| 
| ||||||
 – канонические уравнения – канонические уравнения
| |||||||
| КРИВЫЕ ВТОРОГО ПОРЯДКА | |
| Определение эллипса. | Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая расстояния между фокусами и равная 2a. |
 |
a – большая полуось эллипса;
b – малая полуось эллипса;
F1(– с,0) и F2 (с,0) – фокусы эллипса;
 , с – фокусное расстояние эллипса;
, с – фокусное расстояние эллипса;
 <1,
<1,  эксцентриситет эллипса;
эксцентриситет эллипса;
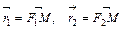 – фокальные радиусы-векторы;
– фокальные радиусы-векторы;
по определению  .
.
Прямые  называются директрисами эллипса.
называются директрисами эллипса.
Каноническое уравнение эллипса 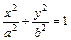 .
.
Строят эллипс, вписывая его в прямоугольник со сторонами длиной 2а и 2b и с центром симметрии в начале координат.
Уравнение эллипса со смещенным при помощи параллельного переноса в точку М0(x0, y0) центром имеет вид
 .
.
Чтобы привести общее уравнение эллипса
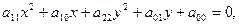 где коэффициенты
где коэффициенты  и
и 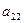
должны иметь одинаковые знаки, к каноническому виду, нужно выделить полные квадраты по переменным x и y.
Например, приведем уравнение кривой
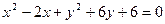
к каноническому виду:

 .
.
Полученное уравнение является каноническим уравнением окружности, радиус которой равен 2, а центр находится в точке М (1,–3).
Признак уравнения окружности:
- коэффициенты при квадратах переменных одинаковые;
- отсутствует произведение переменных.
| Определение гиперболы. | Гиперболойназывается множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами и равная 2а. |
 |
a – действительная полуось гиперболы;
b – мнимая полуось гиперболы;
F1(– с,0) и F2 (с,0) – фокусы гиперболы;
 , с – фокусное расстояние гиперболы;
, с – фокусное расстояние гиперболы;
 >1,
>1,  эксцентриситет гиперболы;
эксцентриситет гиперболы;
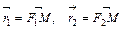 – фокальные радиусы-векторы;
– фокальные радиусы-векторы;
по определению  . Прямые
. Прямые  называются директрисами гиперболы. Уравнения асимптот гиперболы имеют вид
называются директрисами гиперболы. Уравнения асимптот гиперболы имеют вид 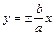 .
.
Каноническое уравнение гиперболы 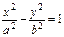 .
.
Строят гиперболу, изобразив предварительно прямоугольник со сторонами длиной 2а и 2b и с центром симметрии в начале координат, а затем вписывают ветви гиперболы в углы между асимптотами гиперболы (прямыми, на которых лежат диагонали прямоугольника), помещая вершины гиперболы в точки с координатами (– а, 0), (а, 0).
Уравнение гиперболы со смещенным при помощи параллельного переноса в точку М0(x0,,y0) центром имеет вид
 .
.
Чтобы привести общее уравнение гиперболы
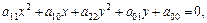 где коэффициенты
где коэффициенты  и
и  должны иметь противоположные знаки, к каноническому виду, нужно выделить полные квадраты по переменным x и y.
должны иметь противоположные знаки, к каноническому виду, нужно выделить полные квадраты по переменным x и y.
Гипербола, уравнение которой  , называется сопряженной по отношению к гиперболе, имеющей уравнение
, называется сопряженной по отношению к гиперболе, имеющей уравнение 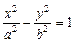 . Фокусы сопряженной гиперболы расположены на мнимой оси.
. Фокусы сопряженной гиперболы расположены на мнимой оси.
| Определение параболы. | Параболойназывается множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемойфокусом,и отданной прямой, называемой директрисой и не проходящей через фокус. |

Каноническое уравнение параболы:  .
.
Строят параболу, откладывая одинаковые отрезки от точек параболы до фокуса с координатами  и до директрисы, уравнение которой
и до директрисы, уравнение которой  . Вершина параболы находится в точке
. Вершина параболы находится в точке  .
.
Уравнение параболы со смещенной при помощи параллельного переноса в точку М0(x0, y0) вершиной имеет вид  .
.
Чтобы привести общее уравнение параболы  к каноническому виду, нужно выделить полный квадрат по переменной y и удвоенный параметр p по переменной х.
к каноническому виду, нужно выделить полный квадрат по переменной y и удвоенный параметр p по переменной х.
Парабола, уравнение которой  , называется сопряженной по отношению к параболе, имеющей уравнение
, называется сопряженной по отношению к параболе, имеющей уравнение  . Фокус сопряженной параболы расположен в точке
. Фокус сопряженной параболы расположен в точке 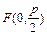 , а ее директриса имеет уравнение
, а ее директриса имеет уравнение  .
.
|
|
|






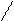 N 1 çç N 2 Û P 1Ç P 2 Û Rang
N 1 çç N 2 Û P 1Ç P 2 Û Rang