 |
Некоторые непрерывные распределения
|
|
|
|
| Название | Плотность распределения | Функция распределения | Матем. ожидание | Дисперсия | Обратная функция для функции распределения | Мода | Медиана | |
| Равномерное | 
| 
| 
| 
| 
| 
| ||
| Распределение Релея | 
| 
| 
| 
| 
| mod =σ | 
-квантиль порядка 
| |
| Гамма-распределение (Г – распределение) | 
| 
| 
| 
|
|
-квантиль порядка
| ||
| Показательное распределение (Г – распределение при α = 1) |  λ>0,
| 
| 
| 
| 
|
|
-квантиль порядка
| |
| Распределение Коши | 
| 
| _ | _ | 
| mod =a | Med=а | |
| Закон арксинуса |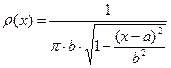 
| 
| а | 
| 
| mod =a | 
| |
| Нормальное распределение | 
| 
| а | 
| mod =a |
|
Интервальная оценка числовых характеристик
| Оцениваемый параметр | Статистика | Плотность распределения | Интегральное уравнение | Решение интегрального уравнения | Доверительный интервал | |
| Математическое ожидание а (дисперсия s2 известна) | 
| Стандартное нормальное
N(0,1)
| 
| Таблица значений функции Лапласа
γ – доверительная вероятность
2ε – длина доверительного интервала
| 
| |
| Математическое ожидание а (дисперсия s2 неизвестна) | 
| Распределение Стьюдента с k=n -1
степенями свободы
|
| Таблица квантилей распределения Стьюдента
| 
| |
| Дисперсия s2 |  с k = n –1 степенями свободы
| Распределение хи -квадрат
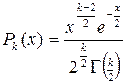с k степенями свободы
| 
|
| s2
 s
| |
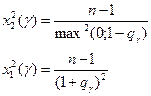
| s2
|
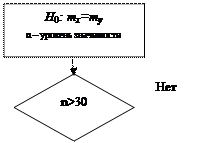
Сравнение двух средних генеральных совокупностей.
(независимые выборки)
I I
 | |||
| |||
|
 |  | ||||
 |
Сравнение двух средних генеральных совокупностей.
|
|
|
(независимые выборки)
|
 | |||||
| |||||
| |||||
 | |||||||||
|
|
|
|
|
|
|
|
|
двусторонняя односторонняя односторонняя
критическая критическая критическая
область область область
| |||||||||||
 | | ||||||||||
 |  |  | |||||||||
МЕТОДЫ ВЫЧИСЛЕНИЙ
Методы простой итерации и Зейделя решения систем линейных уравнений
Пусть дана система линейных алгебраических уравнений, записанная в виде
Допустим, что определитель основной матрицы этой системы не равен нулю, тогда система имеет единственное решение. Для нахождения этого решения можно использовать итерационные методы, в которых решение системы получается как предел последовательности приближений, вычисленных некоторым единообразным процессом.
Для получения итерационных формул метода простой итерации выразим из первого уравнения системы 
, из второго – 
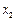, из последнего – 
. Тогда систему можно записать в матричном виде 
, где
, и итерационный процесс организовать по формуле 
.
При таком построении последовательности приближений нужно выяснить условия, при которых последовательность имеет предел. Эти условия дает следующая теорема.
Для того, чтобы процесс итераций сходился к решению системы при любом начальном векторе 
, достаточно, чтобы какая-нибудь норма матрицы В была меньше единицы 
.
Введение нормы дает легко проверяемые условия сходимости метода: 
или 
(в суммах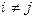 
).
Если условия сходимости не выполнены, то надо преобразовать систему так, чтобы условия выполнялись. Это можно сделать, используя эквивалентные преобразования системы или преобразования следующего вида. Обозначим 
, где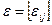 
– матрица с малыми по модулю элементами. Тогда вместо исходной системы будем иметь: 
, где 
, 
.
|
|
|
При достаточно малых 
итерационный процесс должен сходиться.
Если заданная точность вычислений по методу простой итерации w, то вычисления следует проводить до тех пор, пока не выполнится неравенство: 
.
Метод Зейделя представляет собой некоторую модификацию метода простой итерации. Идея его заключается в том, что при вычислении 
-го приближения неизвестной 
учитываются уже вычисленные ранее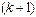 
-е приближения неизвестных 
.
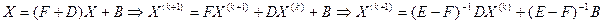
То есть итерационная формула 
, где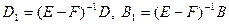 
|
|
|
