 |
Сравнение бесконечно малых функций
|
|
|
|
Пусть  (х) и
(х) и 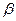 (х) – бесконечно малые функции (б. м. ф.)
(х) – бесконечно малые функции (б. м. ф.)
при х  а, то есть
а, то есть 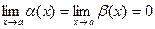 , тогда:
, тогда:
1) 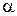 (х) – б. м. ф. более высокого порядка малости по сравнению с
(х) – б. м. ф. более высокого порядка малости по сравнению с  (х) – б. м. ф.
(х) – б. м. ф.
при х  а, если
а, если
 ;
;
2) 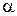 (х) – б. м. ф. более низкого порядка малости по сравнению с
(х) – б. м. ф. более низкого порядка малости по сравнению с  (х) – б. м. ф.
(х) – б. м. ф.
при х  а, если
а, если
 ;
;
3) 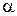 (х) и
(х) и  (х) – б. м. ф. одинакового порядка малости
(х) – б. м. ф. одинакового порядка малости
при х  а, если
а, если
 ;
;
4) 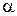 (х) и
(х) и  (х) – б. м. ф., эквивалентные при х
(х) – б. м. ф., эквивалентные при х  а, если
а, если
 a(x)~b(x);
a(x)~b(x);
5) 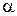 (х) – б. м. ф. k -го порядка малости по сравнению с
(х) – б. м. ф. k -го порядка малости по сравнению с  (х) –
(х) –
б. м. ф. при х  а, если
а, если
 .
.
| Теорема о первом замечательном пределе. | Предел функции 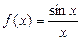 при при  существует и равен единице: существует и равен единице:  . .
|
| Теорема о втором замечательном пределе. | Предел функции  , если , если  ,
и функции ,
и функции  , если , если  , существует и равен числу , существует и равен числу 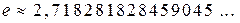 : :
 . .
|
Применение первого и второго замечательных пределов позволяет доказать справедливость формул в таблице эквивалентных бесконечно малых функций при х  а.
а.

| |||
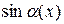 ~ ~ 
|  ~ ~ 
| ||
 ~ ~ 
| 6а |  ~ ~ 
| |
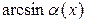 ~ ~ 
| 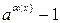 ~ ~ 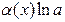
| ||
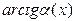 ~ ~ 
| 7а |  ~ ~ 
| |
 ~ ~ 
|  ~ ~ 
|
Замечание. В случаях, когда аргумент α(х) функции в вычисляемом пределе стремится не к нулю, а к отличному от нуля числу, например, α(х)  а, а
а, а  0, вводят новую переменную
0, вводят новую переменную
t = α(х) – а.
Тогда, если α (х)  а, то t
а, то t  0 (функция t (х) должна быть непрерывной функцией в окрестности точки t = 0).
0 (функция t (х) должна быть непрерывной функцией в окрестности точки t = 0).
Новая переменная t  0 (при α(х)
0 (при α(х)  а), и для нее легко можно использовать таблицу эквивалентных бесконечно малых функций.
а), и для нее легко можно использовать таблицу эквивалентных бесконечно малых функций.
Например, вычислим предел
 Предварительно сделаем следующие преобразования:
Предварительно сделаем следующие преобразования:


 при
при 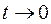
и воспользуемся результатами преобразований:
= 

Бесконечно большие функции (б. б. ф.), так же как и бесконечно малые, можно сравнивать между собой.
Если предел отношения двух бесконечно больших функций равен:
1. Бесконечности, тогда в числителе – б. б. ф. более высокого порядка роста;
|
|
|
2. Нулю, тогда в числителе – б. б. ф. более низкого порядка роста;
3. Постоянному числу, не равному нулю или единице, тогда эти бесконечно большие функции одинакового порядка роста;
4. Единице, тогда бесконечно большие функции эквивалентны.
Полезно иметь в виду, что при вычислении пределов отношений конечного числа б. б. ф. складываемых функций слагаемые более низкого порядка роста можно отбрасывать, а сумму заменять слагаемым самого высокого порядка роста.
При  самый высокий порядок роста имеет показательная функция
самый высокий порядок роста имеет показательная функция  ; степенная функция
; степенная функция  имеет порядок роста, более низкий по сравнению с показательной функцией, но более высокий по сравнению с логарифмической; логарифмическая функция
имеет порядок роста, более низкий по сравнению с показательной функцией, но более высокий по сравнению с логарифмической; логарифмическая функция  имеет самый низкий порядок роста по сравнению и с показательной функцией, и со степенной. Это обозначают так:
имеет самый низкий порядок роста по сравнению и с показательной функцией, и со степенной. Это обозначают так:
 , при
, при  .
.
Очень эффективным при вычислении пределов оказывается применение следующих правил:
Предел отношения б. м. ф. (б. б. ф.) не изменится, если заменить эти функции эквивалентными.
Разность эквивалентных б. м. ф. (б. б. ф.) есть б. м. ф. (б. б. ф.) более высокого порядка малости (роста) по сравнению с уменьшаемой и вычитаемой б. м. ф. (б. б. ф.).
Сумма конечного числа б. м. (б. б.) слагаемых разного порядка малости (роста) эквивалентна слагаемому самого низкого (высокого) порядка малости (роста).
4. Если б. м. ф. α (x) ~ α 1(x) при x → a, A =const ≠ 0, то A + α (x) ~ A + α 1(x) при x → a.
Например. 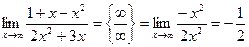 .
.
Чтобы вычислить предел  ,
,
можно воспользоваться основным логарифмическим тождеством
 .
.
Например. 
 .
.
Если же  , то есть в случае неопределенность вида
, то есть в случае неопределенность вида  ,
,
можно применить следующую последовательность тождественных преобразований:
 .
.
Например. 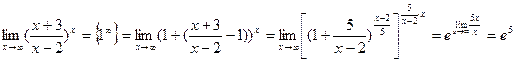 .
.
ТАБЛИЦА ПРОИЗВОДНЫХ
1. 
Степенные функции
2. 
2a. 
2b. 
2c. 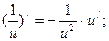
2e. 
( )
)
Показательные функции
|
|
|
3. 
3a. 
Логарифмические функции
4. 
4a. 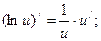
( )
)
Тригонометрические функции
5. 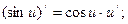
6. 
7. 
8. 
Обратные тригонометрические функции
9. 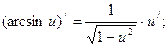
10. 
11. 
12. 
Гиперболические функции
13. 
14. 
15. 
16. 
Показательно – степенные функции
17. 
Модуль функции
18. 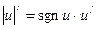 ,
,  ,
,
где  – функция знак u
– функция знак u
(сигнум u).
Правила дифференцирования
1. 
1a. 
2. 
3. 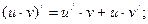
4. 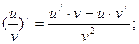
Сложная функция
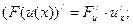
|
|
|


