 |
Интерполяционные многочлены Лагранжа и Ньютона
|
|
|
|
Задача интерполяции заключается в следующем. На отрезке [ a, b ] заданы упорядоченные n+ 1 точки и значения функции в этих точках, т. е. задана таблица значений функции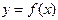 
:
| 
| 
| 
| … | 
|
| 
| 
| 
| … | 
|
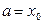
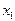
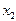
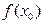
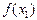
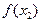
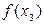
Требуется найти значения этой функции для промежуточных значений аргумента, не совпадающих с приведенными в таблице. Получить аналитическое выражение функции по таблице ее значений в большинстве случаев невозможно. Поэтому вместо нее строят другую функцию 
, которая легко вычисляется и имеет ту же таблицу значений, что и 
, т. е. 
; 
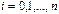Исходная функция называется интерполируемой функцией, а функция 
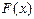– интерполяционной. Значения аргумента в таблице называются узлами интерполяции.
В общем случае полином степени n, принимающий при х = хi заданные значения yi (i= 0, 1,…, n), можно представить интерполяционной формулой Лагранжа
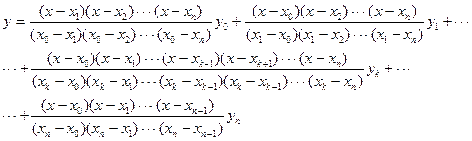
Пусть разности табличных значений аргумента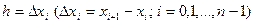 
– постоянные (шаг таблицы). Тогда значение функции y для промежуточных значений х приближенно можно найти при помощи интерполяционной формулы Ньютона
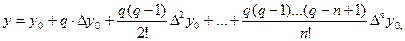
где 
последовательные конечные разности функции y.
Для удобства пользования формулой Ньютона рекомендуется предварительно составить таблицу конечных разностей.
При х = хi полином Ньютона принимает соответственно табличные значения yi.
Погрешность интерполяционной формулы Ньютона приближенно можно оценить по формуле
.
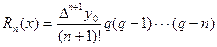Если число n можно взять любым, то его следует выбирать так, чтобы разность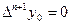 
в пределах данной точности; иными словами, разности 
должны быть постоянными в заданных десятичных разрядах.
Пример. Найти 
, пользуясь табличными данными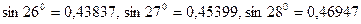 
.
| i | xi | yi | ∆ yi | ∆ 2yi |
| 260 | 0,43837 | -14 | ||
| 270 | 0,45399 | |||
| 280 | 0,46947 |
Здесь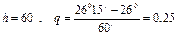 
. Применяя формулу Ньютона, используя первую горизонтальную строку таблицы, имеем 
. Причем погрешность 
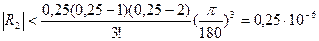. Таким образом, все полученные знаки 
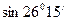─ верные.
|
|
|
Теоретическое обоснование методов хорд и касательных решения трансцендентных уравнений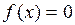 
.
Найдем координаты точки пересечения хорды, соединяющей концы дуги АВ кривой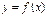 
, с осью абсцисс ОХ (
).
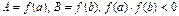Угловой коэффициент хорды АВ равен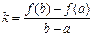 
, поэтому уравнение хорды можно записать так: 
.
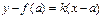В точке 
пересечения хорды с осью ОХ ордината равна нулю, следовательно,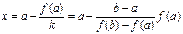 
(☺).
Аналогичным образом из уравнения 
можно получить формулу
(☺☺).
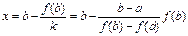Искомый корень уравнения должен находиться на отрезке, ординаты концов которого имеют разные знаки: 
.
Для доказательства сходимости процесса итерации предположим, что корень отделен, и вторая производная сохраняет постоянный знак на отрезке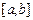 
.
Пусть для определенности 
при 
. Тогда кривая вогнута и, следовательно, расположена ниже своей хорды АВ. Возможны два случая:
1) 
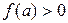и 2)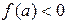 
.
|
|
Заметим, что 1) неподвижен тот конец, для которого знак функции совпадает со
знаком ее второй производной; 2) одна последовательность приближений монотонно убывает и ограничено снизу числом а, а другая – монотонно возрастает и ограничена сверху числом b, поэтому обе последовательности имеют предел, равный искомому корню x уравнения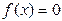 
.
Для организации итерационного процесса решения уравнений методом хорд нужно выяснить, какой конец промежутка отделения корня неподвижен, и применить соответствующую формулу (☺) или (☺☺).
Найдя какое-нибудь приближение корня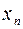 
= x,, положим x = 
и по формуле Тейлора получим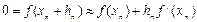 
. Откуда 
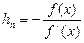. Таким образом, 
– итерационная формула решения уравнений методом касательных.
Можно показать, что погрешность вычислений w оценивается так: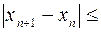 
w.
Литература
1. Араманович И.Г. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / И.Г. Араманович, Г.А. Лунц, Л.Э. Эсгольц. – М.: Наука, 1968.
|
|
|
2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры – M: Наука, 1980, 1984. – 320с.
3. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. М.: Физматиздат, (1969 и позднее).
4. Берман Г.И. Сборник задач по курсу математического анализа. – М.: Физматиздат, издание стереотипное.
5. Боровков А.А. Математическая статистика. Оценка параметров. Проверка гипотез. – М.: Наука, 1984. – 472с.
6. Буколов Э.А., Ефимов А.В., Земсков В.Н. и др. Сборник задач по математике для втузов. Специальные курсы. / Под ред. А.В. Ефимова. – М.: Наука, 1984. – 606с.
7. Бутузов В.Ф., Крутицкая Н.И., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. – М.: Высшая школа, 1993.
8. Вентцель Е.С. Теория вероятностей. – М.: Физматгиз,1962. – 564с.
9. Вентцель Е.С, Овчаров Л.А. Прикладные задачи теории вероятностей. – М.: Радио и связь, 1983. – 416с.
10. Волковыский Л.И. Сборник задач по теории функций комплексного переменного /Л.И. Волковыский, Г.А. Лунц, И.Г. Араманович. – М.: Наука, 1970.
11. Володин Б.Г., Ганин М.П., Динер И.Я. и др. Сборник задач по теории вероятностей, математической статистике и теории случайных функций / Под ред. А.А. Свешникова. – М.: Наука, 1970. – 656с.
12. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1977. – 480с.
13. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979. – 400с.
14. Гнеденко Б.В. Курс теории вероятностей. – М.: Наука,1988. – 448с.
15. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т. 1. – М.: Высш. шк., 1970. – 416 с.
16. Задачи и упражнения по математическому анализу для втузов. /Под ред. Б.П. Демидовича. – М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2004. – 495с.
17. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974. – 296с.
18. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. 1. – М.: Наука, 1971.
19. Каплан И.А. Практические занятия по высшей математике. Ч. I, II, III, Ш, IV, V. Харьков: Издательство Харьковского государственного университета, 1971.
20. Кудрявцев Л.Д. Математический анализ. T.I, Т.2, Т3 – M.: Высш. школа, 1973.
21. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. – М.: Рольф, 2001. – 576с.
|
|
|
22. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 2 курс. – М.: Айрис-пресс, 2004. – 592с.
23. Магазинников Л.И. Теория вероятностей. – Томск.: Изд-во Том. ун-та систем правления и радиоэлектроники, 2000. – 150 с.
24. Никольский С.М. Курс математического анализа. – М.: Наука, 1975.
25. Пантелеев А. В. Теория функций комплексного переменного и операционное исчисление в примерах и задачах /А. В. Пантелеев, А. С. Якимович. – М.: Высш. шк., 2001.
26. Пестова Н.Ф. Неопределенный интеграл. – Томск.: Изд-во Том. Политехнического ун-та, 1995. – 110 с.
27. Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: издание стереотипное (1960 г.и позднее).
28. Привалов И.И. Аналитическая геометрия. – М.: Наука, 1964. – 272с.
29. Пугачёв B.C. Теория вероятностей и математическая статистика. – М.: Наука, 1979. – 496с.
30. Радюк Л.Е., Терпугов А.Ф. Теория вероятностей и случайных процессов. – Томск.: Изд-во гос. ун-та, 1988. – 174с.
31. Румшиский Л.З. Элементы теории вероятностей. – М.: Наука, 1970. – 256с.
32. Севастьянов Б.А. Курс теории вероятностей и математической статистики. – М.: Наука, 1982. – 256с.
33. Тутубалин В.Н. Теория вероятностей. – М.: Изд-во МГУ, 1972. – 230с.
34. Феллер В. Введение в теорию вероятностей и её приложения. Т.1. – М.: Мир, 1964. – 498с.
35. Фукс Б.А. Функции комплексного переменного и некоторые их приложения /Б.А. Фукс, Б.В. Шабат. – М.: Наука, 1969.
36. Хапланов М.Г. Теория функций комплексного переменного/М. Г. Хапланов, – М.: Просвещение, 1965.
37. Хинчин А.Я. Краткий курс математического анализа, – М.: 1955.
38. Чистяков В.П. Курс теории вероятностей. – М.: Наука, 1982. – 256с.
39. Шилов Г.В. Математический анализ (функции одного переменного). Ч. 1-2. – М.: Наука, 1969.
40. Шипачев В.С. Высшая математика. – М.: Высш. шк., 1990. – 479 с.
41. Шнейдер В.Е. и др. Краткий курс высшей математики. Т. 1. – М.: Высш. шк., 1978. –384 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно сходящийся ряд 53, 54
Алгебраическая форма комплексного числа 55
Алгебраический многочлен 21,32
|
|
|
Алгебраическое дополнение 5
Аналитическая функция 56,57
Аргумент комплексного числа 55
Асимптота 29
—гиперболы 19
Базис 7
Бесконечно большая функция 25
— малая функция 23—25
Большая полуось эллипса 18
Вектор 9
Векторная функция43—45
Векторное поле 45
— произведение 9
Вектор-столбец 6
Вектор-строка 6
Величины случайные 62
—дискретные 62
—непрерывные 62
—взаимно независимые 62
— —зависимые 62
Вероятность 60
—безусловная 61
—доверительная 64
—, определение
—,—аксиоматическое 60
—,— геометрическое 60
—,— классическое 60
—,— статистическое 60
Вертикальная асимптота 29
Верхняя сторона поверхности 41
Вершины гиперболы 19
— эллипса 18
Вещественна часть комплексного числа 55
Возрастающая функция 30
Второй замечательный предел 81
Выпуклость вверх (выпуклость) 30
— вниз (вогнутость) 30
Гамма- функция 63, 64
Гармонический ряд 53
Гармоническое поле 45
Геометрический смысл двойного интеграла 38
------ криволинейного интеграла первого
рода 38, 42
------ определенного интеграла 38
------ производной 11
------ смешанного произведения 9
Геометрическое изображение
комплексных чисел 55
------ функции двух переменных 38
Гипербола 19
Гипотеза 61, 65, 66
Главная диагональ матрицы 6
определителя 4
Главное значение аргумента комплексного числа 55
Горизонтальная асимптота 29
Градиент 45
Граница области 54, 57
График 29, 30
Двойной интеграл 38, 39
--------, вычисление путем замены
переменной 39
--------,------- сведения к повторному 39
--------, геометрические приложения 38
--------, физические приложения 38
Двусторонняя поверхность 41
Действительная ось гиперболы 19
Деление отрезка в данном отношении 9
Дивергенция векторного поля 45
Директриса параболы 20
Директрисы гиперболы 19
— эллипса 18
Дисперсия 62
Дифференциал 27, 31, 33, 34
Дифференциальное уравнение 46—49
------- в полных дифференциалах 47
------- высших порядков 48—49
--------------,допускающее понижение порядка 48
-------------- линейное 48,49
----------------- неоднородное 47, 49
--------------------- с постоянными коэффициентами 48,49
----------------- однородное 46, 48
--------------------- с постоянными коэффициентами 48
------ первого порядка 46, 47
------------- линейное 47
----------------- неоднородное 47
----------------- однородное 46, 48
-------------, разрешенное относительно
производной 46,48,50
------ с разделяющимися переменными 46
------ n-го порядка 47, 48
Дифференцирование 26, 32
— обратной функции 26
—, основные правила 26
— простейших элементарных функций 26
— сложной функции 26
—, таблица производных простейших
элементарных функций 26
— функции, заданной параметрически 26
Длина вектора 9
— дуги 33, 35
Дробно-рациональная функция 22, 32
Доверительный интервал 64
|
|
|
Единичная матрица 6
Задача Коши 49
Знакопеременный ряд 53
Знакочередующийся ряд 53
Интегральная кривая 47
— сумма 38, 40, 41, 42
Интеграл с переменным верхним пределом 62
Интегральный признак 53
Интегрирование 27, 31—34
—линейных дифференциальных уравнений
формулами Дюамеля 59
— некоторых иррациональных функций
34 |
трансцендентных функций 31, 34
— непосредственное 27, 31
— подстановкой 27, 33, 34
— полных дифференциалов 37, 56
— по частям 31
— рациональных функций 32
Интенсивность потока 61
Интервал 29
— сходимости степенного ряда 54
Интерполяционная формула Лагранжа 69, 70
------ Ньютона 69, 70
Интерполяционный многочлен 69
Интерполяция 69
Иррациональная функция 21, 34
Испытание 61
Исход благоприятствующий 60
—элементарный 60
Каноническое уравнение
----- гиперболы 19
----- параболы 20
----- эллипса 18
Касательная
— плоскость 37
Квадратная матрица 6
Коллинеарные векторы 10
Компланарные векторы 10
Комплексная плоскость 55
Комплексно сопряженное число 56
Комплексное число 55
Композиция функций (сложная функция) 26
Конечная производная 26, 28
Конечный предел 21—25, 28,
Контур интегрирования 45, 57
Координата точки 9
Координатная плоскость 18—20
— прямая 20
Координатный угол 20
Координаты вектора 9
Коэффициенты степенного ряда 54
— тригонометрического ряда 54
— Фурье 54
Крамер Г. 8, 49
Кратность корня 32, 48
Криволинейная трапеция 35, 38
Криволинейный интеграл 38, 40—45
------- второго рода 38, 41, 43—45
-------. первого рода 38, 40, 42, 44, 45
— Критическая точка 30
Круг сходимости 54
Кусочно-непрерывная функция 54
Левосторонняя (правосторонняя) производная 30
Левая (правая) тройка векторов 9
Левосторонний (правосторонний) предел 54
Линейная функция 10—17
Линейно зависимые функции 7
— независимые функции 7
Линия второго порядка 18—20
— первого порядка 11—15
— (поверхность) уровня 45
Логарифмическая производная 26
Локальный максимум 30
— минимум 30
— экстремум 30
Лопиталь Г. 28
Максимальное значение функции 30
Малая полуось эллипса 18
Масса пластинки 38, 42
— тела 38
Математическое ожидание 62
— —дискретной случайной величины 62
— — непрерывной случайной величины 62
— — случайной функции 62
Матрица 5—7
Мгновенная скорость 26
Медиана 62
Метод вариации постоянной 47, 49
—замены переменной 31—34
—интегрирования по частям 31
—касательных 71,72
—неопределенных коэффициентов 32
— Ньютона 69, 70
— подстановки 31—34
Минимальное значение функции 30
Минор 3, 4
Мнимая единица 55
— ось 55
------- гиперболы 19
— часть комплексного числа 55
Мнимое число 55
Множество 18—20
— значений функции 29, 30
Мода 62
Модуль комплексного числа 55
— числа 26
Момент инерции пластинки 38—40, 42
------- тела 38, 39
Монотонная функция 30
Наклонная асимптота 29
Независимые испытания 61
Неопределенный интеграл 31—34
-----, основные методы интегрирования
31—34
—, —свойства 27
-----, таблица основных интегралов 27
См. также Интегрирование
Непрерывность
— функции в интервале 29, 30
--------- точке 29, 30
------------- слева, справа 29, 30
------ двух переменных 37
------------- вдоль кривой 42,43
------ на отрезке 29,30
Несобственный интеграл второго рода 35, 36
------ первого рода 53, 58
Нижний предел интегрирования 35, 36
Нижняя сторона поверхности 41,43
Нормаль 41, 43
— к поверхности 37
Нормальный вектор плоскости 10, 13, 14
Нулевой вектор 10
Область
— интегрирования 39
— критическая 65, 66
— принятия гипотезы 65, 66
— определения функции 29
— сходимости степенного ряда 54, 58.;
Обратная матрица 7
— функция 26
Обратные тригонометрические функции 26, 31
Общее решение дифференциального
уравненияг47—49
Общий член ряда 53, 54
Объем криволинейного ' цилиндра 53, 54
— — тела 53, 54
вращения 36
Односвязная область 57
Односторонняя поверхность 41, 43
Окрестность точки 29, 30
о малое 23—25
Оператор Гамильтона 45
— Лапласа 45
— «набла» 45
Определенный интеграл 35, 36
------, геометрические и физические
приложения 35, 36
Определитель Вронского 49
— второго порядка 5, 7
— системы уравнений 8
— третьего порядка 4
Ордината 29, 30
Ориентация поверхности 41, 43
Ориентируемая поверхность 41, 43
Ортогональности условия 10
Основной прямоугольник гиперболы 19 |
Особая точка 57
Остаточный член интерполяции 69
Оси гиперболы 19
— координат 10—14
— эллипса 18
Ось 20
— абсцисс 10—20
— аппликат 10—20
— ординат 10—20
— параболы 20
Отрицательное направление
обхода контура 45
Парабола 20
Параметр 11, 12, 15
— параболы 20
Параметрическое задание функции 26
Первообразная 27
Первый замечательный предел 23
Переменная интегрирования 27
Переменные интегрирования 38—45
Перестановки 60
Периодическое продолжение функции 29
Плотность распределения 62
— —, связь с функцией распределения 62
Площадь криволинейного сектора 35
— криволинейной трапеции 35? 36
— плоской фигуры 35, 36
— поверхности 40, 42
вращения 36
— треугольника 9
Побочная диагональ определителя 4, 7
Поверхностный интеграл 38—45
-------- второго рода 41, 43, 44, 45
-------- первого рода 38, 40, 42,
Погрешность 67—72
Подынтегральная функция 33, 34
Подынтегральное выражение 31,
Показательная функция 25, 26, 27
--------- комплексной переменной 55
Поле событий 60
Полная группа событий 61
Полный дифференциал 37
Положительное направление обхода контура
44, 45
Полюс 20
Полярная ось 20
— система координат 20
Полярные координаты точки 20
Полярный радиус 20
— угол 20
Порядок бесконечно большой 25
----------- малой 23, 25
Потенциал 45
Потенциальная функция 45
Потенциальное поле 45
Потенциальный вектор 45
Поток вектора через поверхность 41, 43—45
— событий 61
Правая тройка векторов 9
Правило треугольников 4
Правый предел 29, 30, 54
Произведение независимых случайных величин 62
— событий 61
Пространство элементарных событий 60
Размещения 60
Раскрытие неопределенностей 21—25
Распределение по закону арксинуса 63
— биномиальное 61
— гамма 63
— Коши 63
— нормальное 63
— показательное 63
— Пуассона 61
— равномерное 63
— Релея 63
— Стьюдента 63
Расстояние между двумя точками 9
— от точки до плоскости 14
--------------- прямой 1
Расходящийся ряд 53, 54
Рациональная функция 32, 33
-------- двух переменных 33
Рекуррентная формула 32
Решение дифференциального уравнения 46—49
— системы уравнений 50—52
—,— дифференциальных уравнений 50—52,
Ротор векторного поля 45
Ряд 53,54
— Фурье 54
------- для функций с периодом 54
----------- четных и нечетных функций 54.
Свободный вектор 9
Система трех линейных уравнений 7, 8
с тремя неизвестными 7, 8
—---------------------- однородная 7, 8
Скалярная величина 45
— функция 45
Скалярное поле 45
— произведение 9, 45
Скалярный квадрат 9
Сложная функция 26
Смешанная частная производная 37
Смешанное произведение 9
Событие достоверное 60
— невозможное 60
— простое 60
— случайное 60
События зависимые 61
— независимые 61
— в совокупности 61
— — попарно 61
— несовместные 61
— противоположные 60, 61
— совместные 61
— элементарные 60
Соленоидальное поле 45
Сопряженная гипербола 19
Сочетания 60
Сравнение бесконечно больших 25
------ малых 23—25
—--- выборочной средней с гипотетической генеральной средней нормальной совокупности 65, 66
—--- — дисперсий нормальных генеральных совокупностей 66
—--- — средних нормальных генеральных совокупностей с известными дисперсиями 65
—--- — — — — с неизвестными дисперсиями 66
Статические моменты36,
Степенная функция 26, 27
Степенной ряд 53, 54
------ с комплексными членами 54
Стокс Д. 44, 45
Столбец 4—6
Сторона поверхности 41, 43
Строка 4—6
Сумма векторов 9
— комплексных чисел 55
— матриц 5
— ряда 53, 54
Суперпозиция функций 26
Сферические координаты 39
Схема исследования графика функции 29, 30
Сходящийся ряд 53, 54
Таблица основных интегралов 27
— производных простейших
элементарных функций 26
— — изображений 59
Табличный интеграл 27
— Тейлор Б. 54
Теорема Абеля 54
— Бернулли 61
—дифференцирования оригинала59
— — изображения 59
—интегрирования оригинала 59
— — изображения 59
—Коши 57
— Лапласа интегральная 61
— — локальная 61
— Лопиталя 28
------ о замене переменной в двойном
интеграле 39
------ монотонности функции 30
------ независимости криволинейного
интеграла от пути интегрирования 47, 57
—подобия 59
---- -разложении рациональной
функции на элементарные дроби 32
----- связи между бесконечно большой и я
бесконечно малой функциями |
21, 25
------------- криволинейным и двойным
интегралами 44, 45,
------------- поверхностным и криволинейным интегралами 44, 45
------------- тройным интегралами 44, 45
—смещения в области оригиналов 59
— — — изображений 59
— об общем уравнении прямой 11
—о свертке оригиналов 59
Теоремы о бесконечно малых функциях 23—25
------- направлении выпуклости и точках
перегиба графика функции 30
------- первообразных 27
------- пределах функций 21—25
-------- разложении функций в ряд Фурье 54
-------- сведении двойного интеграла к
повторному 39
-------- свойствах решений линейных
дифференциальных уравнений 47—49
-------- свойстве эллипса и гиперболы 18, 19
-------- сходимости степенных рядов 54
------------ числовых рядов 53
— об абсолютных величинах 26
--------- интегрируемости функций 27, 31—35, 38—45
--------- экстремумах функций 30
Точка возможного экстремума 30
— локального максимума 30
минимума 30
экстремума 30
— перегиба 30
— разрыва 29
------ 1-го рода 54
------ 2-го рода 29
Трансцендентная функция 31
Тригонометрическая форма комплексного
числа 55 '
Тригонометрические функции 26, 27, 33
------- комплексной переменной 55
Тригонометрический ряд 54
Тройной интеграл 38, 39, 44, 45
-------, вычисление путем замены
переменных 39
-------,------- сведения к повторному 39
-------, приложения 38, 39, 44,45
Трубчатое (соленоидальное) поле 45
Убывающая функция 30
Угловой коэффициент 11
Угол между плоскостями 13
------- прямой и плоскостью 14
-------- прямыми 13
— наклона прямой к оси Ох 11
Узлы интерполяции 69, 70
Упорядоченная пара чисел 9
— тройка векторов 9
-------- чисел 9
Уравнение
— Лапласа 45
— линии 10—20
------------ пересекающихся прямых 13
-------- параллельных прямых 13
-------- совпавших прямых 13
— плоскости нормальное 10
общее 10
— поверхности 33
— прямой «в отрезках» 10
--------- нормальное 10
--------- общее 10
---------, проходящей через данную точку, с
данным угловым коэффициентом 11
---------,------- две данные точки 11
--------- с угловым коэффициентом 11
—с двумя переменными 37
См. также Каноническое уравнение
Уравнения линии 10—20
— прямой канонические 11
общие 11
Условие параллельности плоскостей 14, 15
------ прямой и плоскости 13, 14, 15
------ прямых 14
— перпендикулярности плоскостей 13
прямой и плоскости 13
------ прямых 13
Условия Коши 56
Условно сходящийся ряд 53, 54
Уровень значимости 65, 66
Формула Бернулли 61
— для вычисления дисперсии 62
— полной вероятности 61
— Пуассона 61
Формулы Байеса 61
Функция Гаусса 61
— кумулянтная 62
— Лапласа 61
— распределения вероятностей 62
— характеристическая 62
Фурье Ж. 54
Характеристическое уравнение 48
Целая рациональная функция 33-
—часть числа 61 j
Центр гиперболы 19 \
—линии второго порядка 18—20
—масс пластинки 36, 38
—— тела 36, 38
—эллипса 18
Цилиндрическая поверхность 38
Цилиндрические координаты 39
Циркуляция векторного поля 45
Фокальные радиусы точки 18—20
Фокус параболы 20
Фокусы гиперболы 19
— эллипса 18
Формула Грина 45
— замены переменной в неопределенном
интеграле 27
------------- определенном интеграле 35, 36
— интегрирования по частям в
неопределенном интеграле 27, 31
----------------- определенном интеграле
35, 36
— Коши 57
— Ньютона — Лейбница 35, 36
— Остроградского 44,45
— разложения 59
— Стокса 44, 45
Формулы Крамера 8, 49
— Эйлера 55
Функция
— двух переменных 37
— Дирихле 59
— n переменных 37
Частичная сумма ряда 53, 54
Частная производная 37
------ высшего порядка 37
Частное
— комплексных чисел 55
— последовательностей 53
— приращение 37
— решение дифференциального
уравнения 48, 49
Частота 60
Число е 24
Числовой ряд 53
------ с комплексными членами 54
Чисто мнимое число 55
Член ряда 53, 54
Эйлер Л. 55
Эквивалентные бесконечно малые 23—25
Эксцентриситет гиперболы 19
— эллипса 18
Элемент матрицы 4
— множества 60
— объема 38, 39
— определителя 3—5
— площади 38, 39
Элементарные множители 32
—функции 26, 27
Эллипс 18
Якобиан 39
Содержание
стр.
1. Матрицы, определители, системы линейных уравнений....................... 3
● метод окаймляющих миноров........................................................... 3
● алгоритм приведения матрицы к ступенчатому виду...................... 4
● вычисление определителей................................................................ 4
● действия над матрицами.................................................................... 5
● исследование и решение произвольной системы
линейных уравнений.......................................................................... 7
2. Элементы векторной алгебры................................................................. 9
3. Геометрия прямых и плоскостей в таблицах....................................... 10
4. Кривые второго порядка...................................................................... 18
5. Вычисление пределов............................................................................ 21
6. Таблица производных........................................................................... 26
7. Таблица интегралов.............................................................................. 27
8. Приложения производной.................................................................... 28
9. Неопределенный интеграл.................................................................... 31
10. Приложения определенного интеграла................................................ 35
11. Дифференциальное исчисление функции нескольких переменны....... 37
12. Интегральное исчисление функций нескольких переменных.............. 38
13. Дифференциальные уравнения, системы дифференциальных уравнений 46
14. Числовые и функциональные ряды...................................................... 53
15. Теория функций комплексного переменного....................................... 55
16. Операционное исчисление..................................................................... 59
17. Теория вероятностей и математическая статистика............................. 60
● соединения, определения вероятности........................................... 60
● основные теоремы теории вероятностей........................................ 61
● законы распределения случайных величин................................... 62
● некоторые непрерывные распределения........................................ 63
● интервальная оценка числовых характеристик............................. 64
● сравнение двух средних генеральных совокупностей................... 65
18. Методы вычислений.............................................................................. 67
● метод простых итераций и метод Зейделя
решения систем линейных уравнений............................................ 67
● интерполяционные многочлены Лагранжа и Ньютона................. 69
● теоретическое обоснование методов хорд
и касательных решения трансцендентных уравнений................... 71
19. Литература............................................................................................. 73
20. Предметный указатель.......................................................................... 74
Татьяна Васильевна Тарбокова
Сборник справочных материалов
по курсу высшей математики
Учебное пособие
Научный редактор
доктор физико-математических наук,
профессор К.П. Арефьев
Редактор Н.Я. Горбунова
Подписано к печати 6.06.2006 г.
Формат 60 
84/8. Бумага ZOOM.
Печать плоская. Усл. печ. л. 4,48. Уч.-изд. л. 4,05.
Тираж 150 экз. Заказ Цена свободная.
ИФП ТПУ. Лицензия ЛТ №1 от 18.07.94.
 |
Типография ТПУ. 634034, Томск, пр. Ленина, 30.
Ответ автора
учебного пособия
«Сборник справочных материалов по курсу высшей математики»
Тарбоковой Т.В.
на отзывы.
Выражаю искреннюю благодарность своим рецензентам за ценные советы и замечания, а также за доброжелательное отношение к результатам моей работы.
Компьютерные опечатки постараюсь свести к минимуму,
список литературы, состоящий из 41-го источника информации, в «Сборник справочных материалов по курсу высшей математики» добавлен, предметный указатель – тоже.
|
|
|
|
