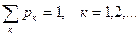 |
Теория вероятностей и математическая статистика
|
|
|
|
| Соединения, определения вероятности | ||||
| Названия, обозначения | Пояснения | Примеры | ||
| С О Е Д И Н Е Н И Я | Перестановки из n элементов Pn = n! = 1∙2∙…∙(n -1)∙ n | Соединения отличаются только порядком элементов. | Число способов поменять местами 10 студентов, стоящих в шеренгу 10! = 1∙2∙…∙10 = 3628800 | |
Перестановки с повторениями
α+β+γ=n
| Соединения из n одинаковых элементов, распределенных по подгруппам из α, β, γ элементов, отличающиеся порядком элементов. | Число способов разбить группу из 12 студентов на подгруппы по 3, 4, 5 человек 
| ||
Размещения
из n элементов по m (n ≤ m)
| Соединения отличаются хотя бы одним элементом или порядком элементов. | Число способов распределить 3 различных обязанности между 10 студентами (по одной обязанности на одного студента)
| ||
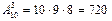
Размещения
из n элементов по m (n ≤ m)
с повторениями
| Соединения содержат любой элемент из m сколько угодно раз от 0 до m. | Число способов распределить 3 различные обязанности между 10 студентами, если один студент может выполнять любое число из них
| ||
Сочетания из n элементов по m
(m ≤ n)
| Соединения отличаются хотя бы одним элементом (порядок элементов не учитывается)
| Число способов распределить 3 студентов из 10 на три одинаковые должности
| ||
Сочетания из n элементов по m
с повторениями
(m может быть больше, чем n)
| Соединения состоят не только из m различных элементов, но и из m каких угодно и как угодно повторяющихся элементов. | Число способов выбрать 6 пирожных в кондитерской, если есть 4 разных сорта пирожных
| ||
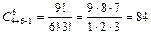
| В Е Р О Я Т Н О С Т Ь | Статистическийподход
| В серии из nk испытаний событие А появилось mk раз;
частота 
обладает свойством устойчивости.
| ||
Классическое определение
| Пространство элементарных событий Ω дискретно и состоит из конечного числа n элементарных равновозможных несовместных событий ω i, называемых случаями. Вероятность P (A) наступления события А равна числу случаев m, благоприятствующих наступлению события А, деленному на число всех возможных исходов n. | |||
Геометрическоеопределение
| Пространством элементарных событий является некоторая область, мера которой mes G, событию А соответствует область, мера которой  .
| |||
Аксиоматическое определение
| Свойства операций над событиями
|
|
|
|
| Основные теоремы теории вероятностей | |||||||||
Ω
 
| У м н о ж е н и я | Зависимыесобытия – наступление одного из них изменяет вероятность наступления другого | 
| ||||||
| |||||||||
| Независимыесобытия – наступление одного из них не изменяет вероятность наступления любого другого и всех возможных их пересечений |
| ||||||||
| |||||||||
| С л о ж е и я | Совместныесобытия содержат общие точки пространства элементарных событий Ω |  
| |||||||
| |||||||||
| Несовместныесобытия не содержат общих точек пространства элементарных событий Ω |
| |||||||
| |||||||||
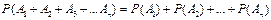
Гипотезы Н i образуют полную группу событий:
| Формула полной вероятности |
| |||||||
| Формула Байеса |
| ||||||||
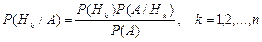
Схема испытаний Бернулли
1 – событие А наступило;
0– событие А не наступило;
 последовательность содержит m единиц и (n-m) нулей.
P (A)= p,
| Формула Бернулли | Формула Пуассона | |||||||
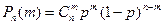Вероятность того, что событие А наступит m раз в серии из n испытаний
|  интенсивность потока λ
| 
| |||||||
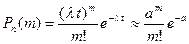
| Наивероятнейшее число m 0 наступления события А | |||||||||
| |||||||||
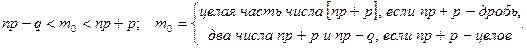
| Локальная теорема Муавра-Лапласа | |||||||||
| |||||||||
| Интегральная теорема Муавра-Лапласа | |||||||||
| |||||||||
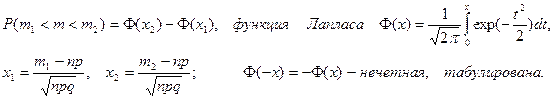
| Законы распределения случайных величин ξ(ω)(ω – случайные события) | |||||||||||||||
| Дискретныеслучайные величины ξ (ω): Ω → R | Непрерывные случайные величины ξ (ω): Ω → R | Свойства | |||||||||||||
| Функция распределения F (x) | Функция распределения F (x) | 
| |||||||||||||
 
| 
| ||||||||||||||
| Квантиль порядка p: η p | Квантиль порядка p: η p | η p существуют для любых случайных величин, обладают свойством устойчивости, легко могут быть измерены. | |||||||||||||
|
| ||||||||||||||
| Медиана – квантиль порядка 0.5 | Медиана– квантиль порядка 0.5 | ||||||||||||||
| Ряд распределения | Плотность распределения ρ (x) |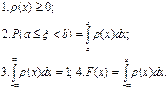 
| |||||||||||||
|
| ||||||||||||||
| Мода ξ | Мода ξ | Унимодальные распределения имеют единственный максимум, полимодальные – два и более. | |||||||||||||
| mod ξ = x (max P) | mod ξ = x (max ρ (x)) | ||||||||||||||
| Начальные моменты порядка к | Начальные моменты порядка к |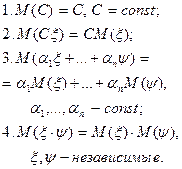 
| |||||||||||||
| 
| ||||||||||||||
| Математическое ожидание ξ: М (ξ) | Математическое ожидание ξ: М (ξ) | ||||||||||||||
| 
| ||||||||||||||
| Центральные моменты порядка к: μ к | Центральные моменты порядка к: μ к | 
| |||||||||||||
| 
| ||||||||||||||
| Дисперсия ξ: D (ξ) | Дисперсия ξ: D (ξ) | ||||||||||||||
| 
| ||||||||||||||
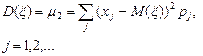
| Характеристическая функция g х(t) | Характеристическая функция g х(t) | 
| |||||||||||||
| 
| ||||||||||||||
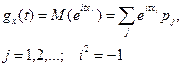
| Кумулянтная функция φ (t) | |||||||||||||||
|
|
|
|
Воспользуйтесь поиском по сайту:
©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...