| №
| Тип дифф. уравнения
|  Вид уравнения Вид уравнения
| Признак уравнения
| Метод решения уравнения
| Результат применения метода
|
|
| Уравнения с разделенными переменными
|

| Функция при  зависит только от зависит только от  , функция при , функция при  зависит только от зависит только от  . .
| Проинтегрировать каждое слагаемое в уравнении.
| Общий интеграл 
|
|
|
Уравнения с разделяющимися переменными
|
 или или
 ; ( ; ( ). ).
| Функции при дифференциалах распадаются на произведения функций, зависящих только от одной из переменных.
| Разделить уравнение на произведение 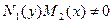 . .
| Уравнение с разделенными переменными и общий интеграл:

|
|
|
Однородные уравнения
|
 или
или
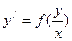 . .
|
Уравнение не изменяет своего вида при замене  и и  на на 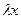 и и  . .
| Сделать замену переменной
 , ,
 , ,
 . .
|
Уравнение с разделяющимися переменными
 . .
|
|
|
Уравнения, приводящиеся к однородным
|
 ; ;
| Производная равна отношению линейных комбинаций переменных
 . .
| 

|
Однородное уравнение
 ; ;
|
|
| Уравнения,
приводящиеся к уравнениям с разделяющимися переменными
|
 ; ;
| Производная равна отношению линейных комбинаций переменных
 . .
|  


| Уравнение с разделяющимися переменными
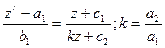
|
|
| Уравнения Лагранжа
| 
|  - известные функции от - известные функции от 
|  линейное ур-ние отн-но х
линейное ур-ние отн-но х
| 
|
|
| Уравнения Клеро
|

|  - известная функция от - известная функция от 
|
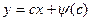
|
Общее решение
|
| №
| Тип дифф. уравнения
|  Вид уравнения Вид уравнения
| Признак уравнения
| Метод решения уравнения
| Результат применения метода
|
|
| Линейные уравнения
|
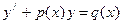

| Искомая функция и её производная входят в уравнение в первой степени и между собой не перемножаются.
| 1. Метод Бернулли
 ; ;  2.Метод вариации произвольной постоянной
2.Метод вариации произвольной постоянной
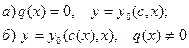
| 1.  Система двух ДУ с разделяющимися переменными
2.ДУ с разделяющимися переменными
Система двух ДУ с разделяющимися переменными
2.ДУ с разделяющимися переменными
|
|
|
Уравнения Бернулли
|
 или
или
 . .
| Левая часть уравнения – такая же, как у линейного уравнения, а правая отличается на сомножитель: искомую функцию в степени m.
| 1.Метод Бернулли
 ; ; 
 2.
2. 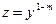 , ,
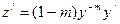
| 1.Система двух ДУ с разделяющимися переменными
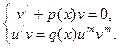 2.Линейное уравнение
2.Линейное уравнение

|
|
|
Уравнения в полных дифференциалах
|

|
Условие полного дифференциала
 . .
|
1.  .
2. .
2. 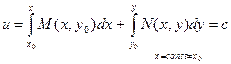 или
или
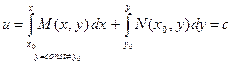
|
Общий интеграл.
|
|
| Приводящиеся к уравнению в полных диф.
|

|

| 
| 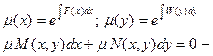 уравнение в полных дифф-лах
уравнение в полных дифф-лах
|
| №
| Тип уравнения
| Вид уравнения
| Признак уравнения
| Метод решения уравнения
|
|
| Допускает понижение порядка
| 
| Ур-ние записано явно относительно старшей производной;
в правой части ур-ния ф-ция зависит только от х.
|
Последовательное понижение порядка производной
n -кратным интегрированием

|
|
| Допускает понижение порядка
| 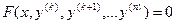
| Уравнение не содержит явно искомой функции y и её первых производных до порядка k-1 включительно
|
Понижение порядка уравнения на k единиц заменой переменной
 , ,  ,…., ,….,  . .
|
|
| Допускает понижение порядка
| 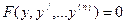
| Уравнение не содержит явно независимой переменной х
| Понижение порядка уравнения на единицу заменой переменной
 и так далее. и так далее.
|
|
| Линейное однородное уравнение с постоянными коэффициентами (ЛОДУ)
| 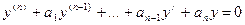
| Искомая функция и все её производные входят в уравнение в первой степени и между собой не перемножаются; правая часть уравнения равна нулю.
| Нахождение корней характеристического уравнения
 .
Каждому действительному корню k кратности r характеристического уравнения соответствует r линейно независимых частных решений ЛОДУ: .
Каждому действительному корню k кратности r характеристического уравнения соответствует r линейно независимых частных решений ЛОДУ:  Каждой паре комплексных корней
Каждой паре комплексных корней  кратности s хар-кого ур-ния соответствует 2 s линейно нез-мых Ч.Р. ЛОДУ: кратности s хар-кого ур-ния соответствует 2 s линейно нез-мых Ч.Р. ЛОДУ: 
 Если
Если  , то , то  ОР ЛОДУ
ОР ЛОДУ 
|

 Вид уравнения
Вид уравнения

 зависит только от
зависит только от  , функция при
, функция при  зависит только от
зависит только от  .
.

 или
или
 ; (
; ( ).
).
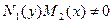 .
.

 или
или
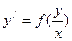 .
.
 и
и  на
на 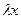 и
и  .
.
 ,
,
 ,
,
 .
.
 .
.
 ;
;
 .
.


 ;
;
 ;
;
 .
.




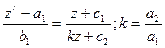

 - известные функции от
- известные функции от 
 линейное ур-ние отн-но х
линейное ур-ние отн-но х


 - известная функция от
- известная функция от 
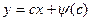
 Вид уравнения
Вид уравнения
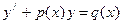

 ;
;  2.Метод вариации произвольной постоянной
2.Метод вариации произвольной постоянной
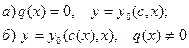
 Система двух ДУ с разделяющимися переменными
2.ДУ с разделяющимися переменными
Система двух ДУ с разделяющимися переменными
2.ДУ с разделяющимися переменными
 или
или
 .
.
 ;
; 
 2.
2. 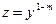 ,
,
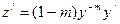
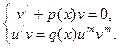 2.Линейное уравнение
2.Линейное уравнение


 .
.
 .
2.
.
2. 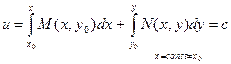 или
или
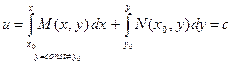



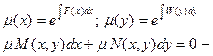 уравнение в полных дифф-лах
уравнение в полных дифф-лах


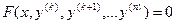
 ,
,  ,….,
,….,  .
.
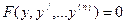
 и так далее.
и так далее.
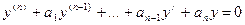
 .
Каждому действительному корню k кратности r характеристического уравнения соответствует r линейно независимых частных решений ЛОДУ:
.
Каждому действительному корню k кратности r характеристического уравнения соответствует r линейно независимых частных решений ЛОДУ:  Каждой паре комплексных корней
Каждой паре комплексных корней  кратности s хар-кого ур-ния соответствует 2 s линейно нез-мых Ч.Р. ЛОДУ:
кратности s хар-кого ур-ния соответствует 2 s линейно нез-мых Ч.Р. ЛОДУ: 
 Если
Если  , то
, то  ОР ЛОДУ
ОР ЛОДУ 


