 |
Исследования функции с применением производных
|
|
|
|
| № п/п | Цель исследования | Действия и вывод | ||||
| Найти интервалы монотонности и точки локальных экстремумов функции | 1.1.1. Найти критические точки первого порядка 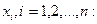
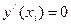 или или 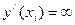 , или , или 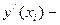 не существует
(необходимоеусловие существования экстремума функции в точке);
1.2.1. Применить первое достаточное условие существования экстремума функции в критической точке: не существует
(необходимоеусловие существования экстремума функции в точке);
1.2.1. Применить первое достаточное условие существования экстремума функции в критической точке:
| |||||

| 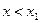
| 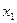
| 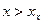
| |||
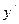
| ¾ | Критическая точка первого порядка | + | |||
| y | Функция убывает | 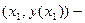 точка минимума точка минимума
| Функция возрастает | |||

| 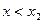
| 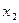
| 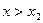
| |||
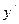
| + | Критическая точка первого порядка | ¾ | |||

| Функция возрастает | 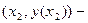 точка максимума точка максимума
| Функция убывает | |||
1.2.2. Если 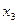 и и 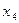 – стационарные точки (все производные до (2к –1) порядка равны нулю), можно применить второе достаточное условие существования экстремума функции в точке: – стационарные точки (все производные до (2к –1) порядка равны нулю), можно применить второе достаточное условие существования экстремума функции в точке:
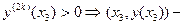 точка локального минимума; точка локального минимума;
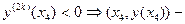 точка локального максимума; точка локального максимума;
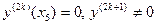 – в точке – в точке 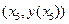 экстремума нет. экстремума нет.
| ||||||
| Найти интервалы выпуклости и вогнутости графика функции и точки перегиба | 2.1. Найти критические точки второго порядка  : :
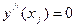 или или 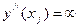 , или , или 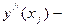 не существует
(необходимое условие существования точки перегиба графика);
2.2. Применить достаточныеусловия выпуклости и вогнутости графика и существования точек перегиба: не существует
(необходимое условие существования точки перегиба графика);
2.2. Применить достаточныеусловия выпуклости и вогнутости графика и существования точек перегиба:
| |||||

| 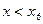
| 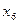
| 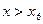
| |||
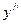
| + | Критическая точка второго порядка, точка непрерывности | ¾ | |||

| График функции вогнутый | 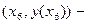 точка перегиба точка перегиба
| График функции выпуклый | |||
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Метод непосредственного интегрирования
 |



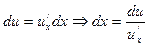
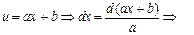
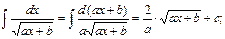
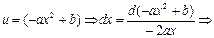
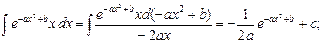
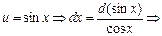
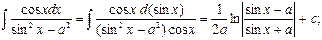
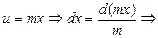
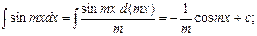
Метод интегрирования по частям
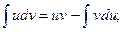
| № п/п | Интеграл | Разбиение подынтегрального выражения на части | 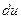
| v | Результат применения метода |
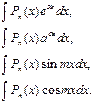
| 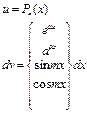
|
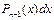
| 
| Метод применяют n раз, пока степень многочлена не понизится до нулевой | |
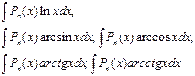
| 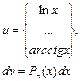
| 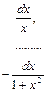
|
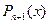
| Получают интеграл от функций степеней х | |
Циклические интегралы:
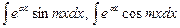
| 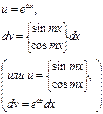
| 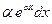
|  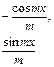
| Метод применяют 2 раза, получая уравнение относительно искомого интеграла |
|
|
|
План интегрирования рациональных дробей
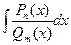 .
.
Рn (x) = a 0x n + a 1x n-1 + a2x n-2 + …….+ a n ,
Qm (x)= b0xm + b1xm-1 + b2xm-2 + ……. + bm .
 I.
I. 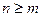 – дробь неправильная;
– дробь неправильная; 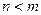 – дробь правильная
– дробь правильная  (степень Рn (x) меньше)
(степень Рn (x) меньше)
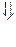 (степень n Рn (x) больше или равна степени m Qm (x))
(степень n Рn (x) больше или равна степени m Qm (x))


 Рn (x) Qm (x)
Рn (x) Qm (x) 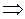
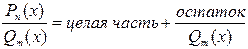
 …… целая часть
…… целая часть
rs (x) – остаток (s<m) 
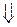
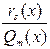 – прав. дробь.
– прав. дробь.
II. Знаменатель Qm (x) разложить на множители линейные – (x-a) и квадратичные – (x2+px+q). Правильную дробь разложить на сумму простых дробей в зависимости от множителей знаменателя.
| Вид множителя в знаменателе дроби | Сколько дробей | Сумма простых дробей, соответствующая множителю в знаменателе правильной рациональной дроби |
| (x-a) k | k | 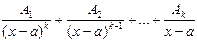
|
| (x2+px+q) w | w | 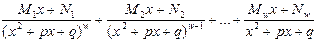
|
III. Найти неопределенные коэффициенты A, M, N, приведя сумму дробей к общему знаменателю и приравняв числители исходной правильной дроби и суммы дробей.
IV. Проинтегрировать простые дроби:
а) дроби первого типа 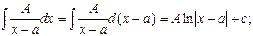
б) дроби второго типа 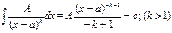
в) дроби третьего типа 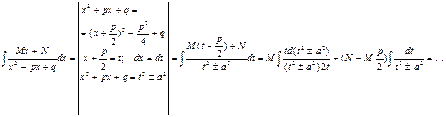
г) дроби четвертого типа 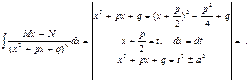
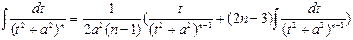 – рекуррентная формула
– рекуррентная формула
Интегрирование тригонометрических и гиперболических функций
| № п/п | Подынтегральная функция | Подстановка | Вспомогательные преобразования | Итог |
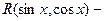 рациональная функция относительно
sin x,
cos x рациональная функция относительно
sin x,
cos x
| Универсальная
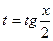
| 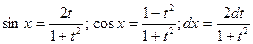
| Подынтегральная функция рациональная относительно х | |
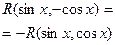 Нечетная относительно
сos x
Нечетная относительно
сos x
| 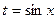
| 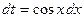
| ||
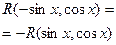 Нечетная относительно
sin x
Нечетная относительно
sin x
| 
| 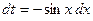
| ||
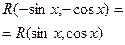 Четная относительно
сos x и sin x
Четная относительно
сos x и sin x
| 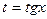
| 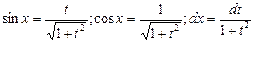
| ||
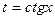
| 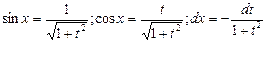
| |||
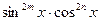 Степени четные неотрицательные
Степени четные неотрицательные
| 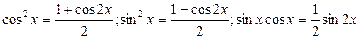
| Понижение степени | ||
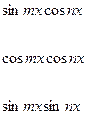
| 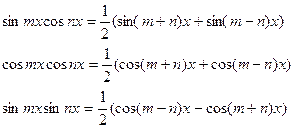
| Сумма функций | ||
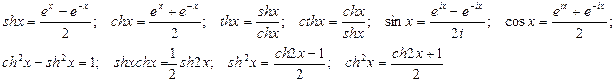 Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций
Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций
|
|
|
|
|
|
|


