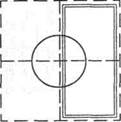
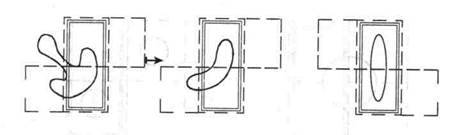
Изменения в проверяемых гипотезах при проверке карточек

1. Первый шаг решения задачи — выдвижение гипотезы. Два испы­туемых — «Флуранс» и «Брока» — сформулировали на базе первого положительного примера соответственно целостную и парциальную гипотезы. Подчеркнем, что в методике Брунера испытуемый имеет

дело (если, конечно, он правильно понял инструкцию и выполняет ее) не с объемом искусственного понятия, а с его содержанием — 4 возможными признаками. Тем самым целостная гипотеза (для при­веденного случая) будет следующей: «1 черный квадрат с 1 каемкой» (рис. 6). Парциальная же гипотеза имеет варианты, например «квадра­ты» или «1 фигура» (рис. 7). Гипотезы идеальны в смысле крайнего различия между ними: либо все поле возможных признаков, либо только один из них. После выдвижения начальной гипотезы все будущие при­меры получают для испытуемого новое измерение. Теперь они могут относиться или нет не только к задуманному понятию (и быть соот­ветственно положительными или отрицательными), но и к сформу­лированной гипотезе, т. е. подтверждать или опровергать ее. Тем са­мым, примеры могут быть положительными подтверждающими (ПП), отрицательными подтверждающими (ОП), положительными опровер­гающими (ПО), отрицательными опровергающими (00).

2. Второй шаг решения задачи — использование стратегии. Начиная со второго полученного примера, испытуемый применяет определен­ную стратегию обработки информации, которая для наших типологи­чески разных случаев определяется характером сформулированной гипотезы. Рассмотрим, какими стратегиями будет пользоваться каж­дый из испытуемых, если их способ приема и обработки информации остается неизменным.

3. Целостная гипотеза — стратегия фокусировки. Общим правилом любой стратегии будет, по-видимому, сохранение гипотезы при встрече с подтверждающим ее примером. Для целостной гипотезы такими бу­дут любые отрицательные примеры (единственным ПП-примером является первая предъявленная карточка). Изменить же свою гипотезу данный стратег вынужден при встрече с ПО-примером, скажем, «2 черных квадрата с 1 каемкой». В этом случае он сохраняет общие части гипотезы и примера, как бы «срезая» нерелевантный признак —

 

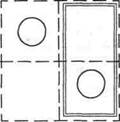
Рис. б. Пример использования при- Рис. 7. Пример использования при­
знаков в целостной гипотезе.             знаков в парциальной гипотезе.

-------- гипотеза; === понятие; ----------------- положительный пример.

 

число фигур (рис. 8). Подобным образом он будет действовать при встре­че с новым ПО-примером («1 черный квадрат с 2 каемками» — рис. 9). Данная стратегия названа «фокусировкой»: задействовав все поле воз­можных признаков, испытуемый постепенно устраняет лишние. При­меры, приводящие к изменению (уточнению) гипотезы, назовем ин­формативными: для фокусировки это ПО-примеры. Интересно, что ОО-примеров для стратегии фокусировки просто нет (ведь в целост­ной гипотезе учтены все возможности).

4. Парциальная гипотеза — стратегия сканирования. Понятно, что и здесь примеры, подтверждающие гипотезу, также не будут инфор­мативными. Для парциальной гипотезы (скажем, «квадраты») таких примеров будет больше: это ОП- (как и для целостной) и ПП-при-меры, в том числе — «2 черных квадрата с 1 каемкой» и «1 черный квадрат с 2 каемками». Данный стратег изменяет свою гипотезу толь­ко при встрече с ОО-примером, включающим угаданный релевант­ный признак в сочетании с другими, нерелевантными (напомним, что понятия конъюнктивны). Так, в ответ на пример «1 красный квад­рат с 1 каемкой» испытуемый должен соотнести его с содержанием предыдущих примеров (прежде всего положительных) и провести их логический анализ. Успешным итогом этого анализа будет расшире­ние первоначальной гипотезы — скачок (включение в нее второго релевантного признака — цвета фигур) (рис. 10). Эта стратегия назва­на «сканированием». В приводимом нами случае («черные квадраты» — понятие с 2 признаками) испытуемому нужно было сделать всего один такой «полезный» скачок. Если понятие содержит 1 признак, испытуемый имеет возможность угадать его сразу, но если этого не случится (и если признаков больше — 2 или 3), он должен удержи­вать в памяти содержание предыдущих примеров. Данному стратегу может и не повезти, когда первая гипотеза (здесь — «1 квадрат») не

Рис. 8. Уменьшение числа признаков при Рис. 9. Уменьшение числа
целостной гипотезе (встреча с ПО-приме-     признаков при встрече

ром).                                                          со вторым ПО-приме-

ром.

------ гипотеза; ^= понятие; -------- положительный пример.

Рис. 10. Включение новых признаков в   Рис. 11. Изменение парциаль-
гипотезу при сканировании (встреча       ных гипотез при встрече с

отрицательный пример.

с ОО-примером).                                   ПО-примером.

■ гипотеза; = понятие; - - положительный пример;

входит в задуманное понятие. Тогда информативными становятся ПО-примеры, скажем «2 черных квадрата с 1 каемкой», требующие отказа от нее и выдвижения новой (рис. 11). Поэтому путь к задуман­ному понятию может оказаться полным перебором всех признаков первого положительного примера с последующим отказом от нере­левантных: испытуемый должен совершить столько же «скачков», сколько релевантных признаков осталось неучтенными в первой пар­циальной гипотезе.

Обоснование оптимальной работы испытуемого. 1. Общее число ги­потез. Попробуем оценить общее число гипотез, которые могут быть у испытуемого перед началом эксперимента. Составим прежде всего полную матрицу возможных сочетаний признаков для различных се­рий эксперимента, включив в нее также и не встречающийся в дан­ном эксперименте случай понятий из четырех признаков.

Из табл. 1 видим, что существует 4 сочетания признаков по одно­му, 6 — по два, 4 — по три и 1 — по 4 признака. Всего имеются 15 сочетаний. Теперь, приняв во внимание то обстоятельство, что каж­дый из признаков независимо от других может принимать три значе­ния, нетрудно подсчитать число гипотез, соответствующих каждому из четырех наборов признаков и их общее число:

1 признак — 4-3 — 12 гипотез;

2 признака — 4-3-3 — 36 гипотез;

3 признака — 4-3-3-3 = 108 гипотез;

4 признака — 1-3-3-3-3 = 81 гипотеза. Итого: 237 гипотез.

1. Матрица возможных сочетаний признаков

(строки 1-4 для одного признака, 5-10 для двух, 11—14 для трех, 15 — для четырех признаков)

 

№ п/п	Цвет фигур	Форма фигур	Число фигур	Число каемок
	0 0	0 0 1 0	0 1 0 0	1 0 0 0
5 6 7 8 9 10	0 0 0 1 1 1	0 1 1 0 0 1	1 0 1 0 1 0	1 1 0 0 0
12 13 14	1 1 1	1 0 1 1		1 1 1

Понятно, что общее число возможных карточек-примеров в дан­ном случае равно числу всех гипотез с 4 признаками, т. е. 81. Именно столько карточек и составляет стимульный материал в методике Бру-нера. Каждому понятию с одним признаком соответствует 27 карто­чек-примеров, с двумя признаками — 9 карточек, с тремя — 3, а с четырьмя — 1.

2. Сокращение числа гипотез и информативность различных примеров. Рассмотрим теперь, каким образом будет сокращаться число возмож­ных для испытуемых гипотез о содержании задуманного эксперимен­татором понятия при последовательных встречах с различными при­мерами. Легко видеть, что первый же положительный пример (лю­бой! ) устраняет 80 гипотез с четырьмя признаками, 104 — с тремя, 30 — с двумя и 8 — с одним. Иначе говоря, выбор испытуемого после встречи с первым положительным примером ограничивается 1+4 + 6 + 4=15 гипотезами (понятно, что их число равно числу всех возможных сочетаний признаков — табл. 2). Важно также заметить, что число гипотез, остающихся после встречи с первым положитель­ным примером, не зависит от содержания задуманного понятия.

На втором шаге работы испытуемого он может встретиться как с положительными, так и с отрицательными примерами, причем — с положительными, совпадающими с первым примером по одному, двум или трем признакам, а с отрицательными — отличающимися от первого по одному, двум, трем или всем четырем признакам. Число гипотез, устраняемых в каждом из этих случаев, дано в таблице. 90

2. Число гипотез, устраняемых на втором шаге испытуемого, при встрече с различными типами примеров

 

------------------------------------------------------------------------------------- Пример	Количество устраняемых гипотез
1. Положительный, совпадающий с первым по одному признаку Отрицательный, совпадающий с первым по одному признаку
2. Положительный, совпадающий с первым по двум признакам Отрицательный, совпадающий с первым по двум признакам
3. Положительный, совпадающий с первым по трем признакам Отрицательный, совпадающий с первым по трем признакам
4. Отрицательный, различающийся с первым по четырем признакам

Из табл. 2 видно, что на втором шаге работы испытуемого различ­ные типы встречаемых им примеров существенно различаются по числу гипотез, которые они позволяют устранить при рациональной работе испытуемого. Наиболее «информативными» являются примеры пер­вого типа — такой пример позволяет устранить все гипотезы, кроме одной, и, таким образом, уже на втором шаге отгадать задуманное понятие. Наименее информативными, пустыми, оказываются отри­цательные примеры первого типа — они не позволяют устранять ни одной гипотезы. Легко заметить, что пустых или комплементарных положительных примеров быть уже не может.

На очередном, третьем шаге работы испытуемый может встретить уже только три типа примеров, совпадающих/различающихся по од­ному или двум признакам, а также пустые. Причем встреча с положи­тельным примером, совпадающим, или с отрицательным, различаю­щимся с первым по одному признаку, снова ведет к решению задачи. Наконец, на четвертом шаге испытуемый может встретиться или с пустым примером, или же с примером, совпадающим/отличающим­ся по одному признаку, и, таким образом, даже в случае наиболее неблагоприятных примеров на предыдущих шагах отгадать задуман­ное экспериментатором понятие. Иначе говоря, если не считать пус­тых примеров, рационально действующий испытуемый непременно решит задачу за четыре шага. Это и есть минимальное «логически не­обходимое» число непустых примеров, которое гарантирует уверен­ное решение задачи даже в наиболее неблагоприятном случае.

Идеальные и реальные стратегии. Из разбора шагов, ведущих к последовательному сокращению числа альтернативных гипотез, мож­но увидеть, что всегда существует некоторая идеальная (рациональ­ная) стратегия, с необходимостью приводящая к решению постав­ленной задачи. В данном случае нетрудно было опознать стратегию фокусировки. Было бы неверным, однако, считать, что это единствен-

ная идеальная стратегия, ведущая к решению задачи, или даже что она наиболее эффективна в любом случае. Применение всякой иде­альной стратегии позволяет достигать конкретных целей, которыми (в разных случаях) могут становиться: 1) максимизация получаемой информации; 2) снижение нагрузки на память и логическое члене­ние; 3) образование данного понятия за минимальное число шагов; 4) сведение к минимуму числа ошибочных, гипотез в процессе обра­зования понятия; 5) достижение субъективной уверенности в пра­вильном образовании понятия вне зависимости от числа примеров, с которыми встретился испытуемый, и др.

Понятие идеальных стратегий является средством анализа и опи­сания реальной работы испытуемого в эксперименте. Оно не только задает единицу анализа процесса образования понятия, позволяя рас­сматривать отдельные шаги этого процесса как необходимые и неса­мостоятельные моменты целого, но также открывает путь для иссле­дования разнообразных зависимостей, существующих между отдель­ными составляющими ситуации.

Типы реальных стратегий представляют собой качественные зна­чения зависимой переменной в экспериментах по образованию ис­кусственных понятий. Умение правильно идентифицировать рассмот­ренные стратегии является критерием освоения методики Брунера. Если цель достигнута, можно приступить к постановке и решению соб­ственно исследовательских вопросов о факторах, определяющих вы­бор той или иной стратегии. Пример такого использования методики в исследовательских целях дает задание № 11 в разделе «Эксперимен­тальный метод» исследовательского практикума.

Литература: 10; 15.

Задание 12. Использование теории информации
§ 14            ^в модифицированном варианте методики

образования искусственных понятий

Тема задания

Знакомство с модификацией методики образования искусствен­ных понятий, предложенной О. К. Тихомировым.

Введение

Информация как количественное понятие имеет смысл только как результат осуществления какого-либо события, имеющего некоторую вероятность. Вероятностные же свойства объектов в экспериментах Дж. Брунера не анализировались и не являлись предметом исследова-

ния. Эксперименты проводились с испытуемыми однократно. Целью их было только посмотреть, какую стратегию выберет испытуемый в зависимости от варьирования некоторых условий. В таком экспери­менте, естественно, нельзя было ставить вопрос о том, могут ли ис­пытуемые прийти к оптимальной в соответствующих условиях страте­гии в результате тренировки, какими факторами обусловливается из­менение стратегий.

Для того чтобы ответить на эти вопросы, необходимо было изме­нить методику таким образом, чтобы испытуемый находился в ситуа­ции выбора различных информативных элементов в течение длитель­ного времени, что достигается многократным предъявлением ему ог­раниченного набора задач. При таких условиях оказывается возможным выяснить, чем обусловливается его поисковая деятельность, вскрыть факторы, определяющие и регулирующие ее осуществление.

Модификация методики О. К. Тихомировым. Соответствующая ме­тодика была предложена О. К. Тихомировым. Задачей исследований О. К. Тихомирова [1969] являлось изучение закономерности самостоя­тельного решения человеком задач с неопределенностью, т. е. задач, ре­шение которых может заканчиваться различным результатом, и следо­вательно, до нахождения решения существует известная неопределен­ность относительно конечного результата задач на распознавание явлений.

Для этой цели было применено сопоставление хода реального процесса решения мыслительной задачи на классификацию с опти­мальным способом ее решения, выводимым на основании специаль­ных математических расчетов, в результате чего оказывается возмож­ным получить некоторую характеристику реального процесса.

Использованная методика была во многих отношениях сходной с методикой образования искусственных понятий в варианте Выгот­ского—Сахарова. И в том, и в другом случае задача испытуемого зак­лючается в нахождении методом последовательных проб принципа классификации, избранного экспериментатором. Если же рассматри­вать группы объектов, которые в результате классификации должен был выделить испытуемый по аналогии с образованием искусствен­ных понятий (определение каждой группы рассматривать как образо­вание искусственного понятия), то основное отличие данной методи­ки от методики Выготского—Сахарова заключается в том, что осно­вание такой классификации является переменным, — центральный момент методики О. К. Тихомирова. Именно переменный характер клас­сификации объектов позволил использовать для описания оптималь­ных способов решения задач методы теории вероятности и теории информации, так как это приводило к созданию статистической ха­рактеристики обследуемых объектов. С описанной модификацией ме­тодики Выготского—Сахарова студенты должны ознакомиться в на­стоящем задании.

Цель задания — применить использование теории информации для изучения процесса образования искусственных понятий.

Статистическая структура обследуемого поля. В методику входит весь набор стимульного материала, и указаны наборы карточек, кото­рые рекомендуется использовать в опытах.

В качестве наборов гипотез предлагается рассмотреть те 3 набора, которые представлены ниже, в разделе «Экспериментальный матери­ал» с 2, 4 и 14 объектами в группе.

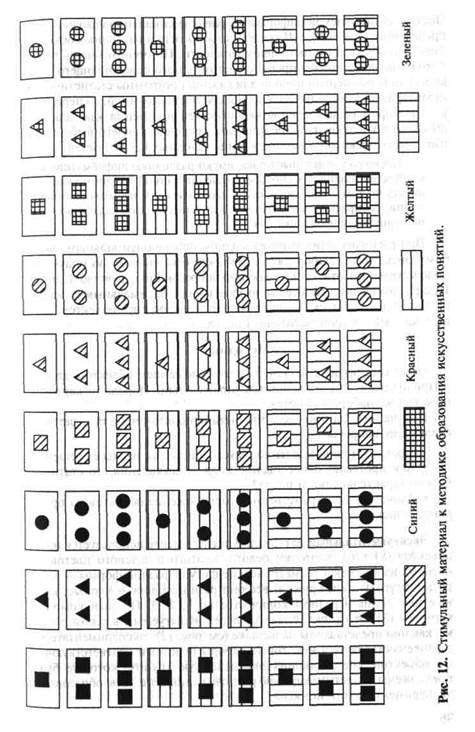
При заданных условиях в длинном ряду лредъявлений стимульных объектов (карточек) (рис. 12) каждая гипотеза может реализоваться (со­ответствовать предъявляемым карточкам) в среднем одинаковое чис­ло раз. Следовательно, вероятность реализации для каждой гипотезы равна: для I набора />, = Р₂ = '/₂; для II набора ^ = Р₂- Р_} = Р₄ = '/₄; для III набора Р= Р₂= Р_ъ=... = Р_ы= '/_м. Очевидно, что чем больше возможных исходов, предъявляемых испытуемому для распознавания гипотез, тем более неопределенен конечный исход решения. Исполь­зуя теорию информации, можно выразить неопределенность опыта более точно. В теории информации показано, что неопределенность опыта — Н, или энтропия, — является функцией числа возможных исходов и вероятности их реализации:

где Р — вероятность отдельного исхода опыта. Если исходы равнове­роятны, то Н = lg₂Af, где М — число возможных исходов опыта.

Таким образом, условия разбираемой нами задачи будут описы­ваться так: 1) Н= lg₂2 = 1 дв. ед.; 2) Я = lg₂4 = 2 дв. ед.; 3) Н— lg₂14 = = 4 дв. ед. В принятых условиях эксперимента каждый из объектов, помимо своих постоянных признаков — количества фигур, нарисо­ванных на карточках, их цвета, формы и фона (или числа каемок), приобретает совершенно определенную статистическую характерис­тику частоты, с которой этот объект оказывается входящим в иско­мую группу при многократном решении задач. Все объекты, таким образом, распределяются на две категории: объекты, которые никог­да не входят в искомую группу; объекты, которые всегда входят в группу с вероятностью больше нуля, но меньше единицы. В связи с тем что объекты помимо своих постоянных признаков в принятых условиях приобретают еще один переменный признак (вхождения или невхождения в искомую группу), каждую отдельную пробу следует рассматривать также как опыт, могущий иметь несколько различных исходов с различной вероятностью их реализации и, следовательно, характеризующийся неопределенностью:

Таким образом, процесс решения задачи выступает как процесс последовательного обследования поля, имеющего некоторую стати­стическую характеристику, а отдельные пробы могут относиться к объектам с различной энтропией появления проверяемого признака.

Поскольку получаемая информация равна уменьшению исходной нео­пределенности: / = Я, — Н₂, результаты проверки различных объектов могут различаться по их информативности. Применим теперь тот же метод к анализу второй пробы с учетом одного осложняющего усло­вия: если перед первой пробой для каждой программы статистическая характеристика обследуемого поля является постоянной, то перед вто­рым выбором распределение вероятностей получения «да» для всех объектов поля зависит от результатов предшествующего выбора, т. е. имеет место некоторое распределение условных вероятностей.

Поскольку отдельные пробы имеют различную информативность, множество различных способов решения данной задачи можно оце­нивать по тому, как соотносятся необходимая и избыточная инфор­мации, собираемые испытуемым, для решения этой задачи при при­менении различных способов.

При распознавании гипотез в одном наборе оптимальным спосо­бом поиска будет выбор любого объекта с вероятностью получения положительного ответа 0, 5, дающий информацию, равную 1 дв. ед. При распознавании гипотез во втором наборе оптимальным способом поиска будет являться последовательный выбор двух объектов, даю­щий каждый соответственно по 1 дв. ед.

Методика

Опыт состоит из 2 частей: 1) с расположением объектов, данном в Приложении; 2) с измененным (произвольно) порядком карточек, но с тем же набором гипотез.

Полученные данные должны быть использованы для ответов на следующие вопросы:

♦ Как влияет неопределенность условий задачи на ход ее решения?

♦ Как протекает обследование поля до выявления его статисти­ческой характеристики и после?

♦ Влияет ли пространственное расположение объектов на проте­кание поиска?

Экспериментальный материал. В эксперименте используется набор объектов (81 шт. ): карточки белого, желтого и зеленого цветов, на которых изображены геометрические фигуры разной формы — квад­раты, треугольники, кружки; все они разного цвета — черные, крас­ные или синие в разном количестве по 1, 2, 3. Полный комплект карточек (81 шт. ) раскладывается перед испытуемым в таком поряд­ке, как они представлены на вкладке (см. рис. 12). Экспериментатором заранее составляются некоторые наборы гипотез и соответствующих им объектов, составляющих определенную группу, которые будут предложены испытуемому для распознавания, т. е. для образования экспериментального понятия.

Возможные наборы гипотез:

I

1. 3 квадрата

2. 3 черные фигуры

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: