 |
Сообщение темы и целей урока
|
|
|
|
Закрепление изученного материала
Задание 1 (с. 8)
Задание 3 (с. 8)
Задание 4 (с. 8)
1) 36: 12 = 3 (м);
2) 3 • 20 = 60 (м).
Задание 6 (с. 8)
40 + 84 + х = 150.
Сначала найдем сумму известных слагаемых и упростим данное уравнение:
40 + 84 = 124;
124 + х = 150.
Теперь нужно найти неизвестное слагаемое.
х = 150-124
х=26
Задание 10 (с. 9)
(15 + 9): 4 = 6 (м.);
6 • 5 = 30 (м.) или 15 + 9 + 6 = 30 (м.).
Подведение итогов урока
6. Домашнее задание: с. 9 № 11(ст. 1, 2)
математика
Тема: Сложение чисел и величин. Изменение суммы в зависимости от изменения ее компонентов.
Цели: повторить алгоритм сложения трехзначных чисел и величин; решать задачи на изменение суммы в зависимости от изменения слагаемых.
Организационный момент
Устный счёт
Соедините примеры с одинаковыми ответами:
7·7 49-15
60-26 28 + 26
6·9 72:9
2·4 76-27
Решите уравнения
х + 38 = 47 52 + х = 70
39 - х=12 х - 18 = 82
Решите задачи:
а) Маме 36 лет, а сыну — 9. Поставьте вопрос к задаче так, чтобы она решалась действием вычитания (деления).
б) На поливку огурцов израсходовали 24 ведра воды, а на поливку помидоров — в 2 раза больше. Сколько всего ведер воды израсходовали на поливку? Сколько литров воды израсходовали, если в каждом ведре было по 10 л?
в*) Мотоциклист проехал 160 км со скоростью 80 км/ч, при этом он несколько раз останавливался в пути. Сколько времени мотоциклист затратил на весь путь, если его остановки заняли 25 мин?
Математический диктант.
Ученики записывают только ответы:
• найдите разность чисел 500 и 70;
• найдите сумму чисел 340 и 60;
• уменьшите 360 в 2 раза;
• увеличьте 420 на 80;
• увеличьте 170 в 3 раза;
• на сколько 290 больше, чем 150?
• на сколько 30 меньше, чем 170?
• найдите произведение чисел 370 и 2;
• найдите частное чисел 280 и 4;
|
|
|
• найдите 1 часть числа 180.
Задание 7 (с. 11)
По условию задачи на доске делается рисунок, где количество станков показано одинаковыми отрезками.
По рисунку сразу видно, что в первом цехе станков стало больше. На сколько? (На 7; 15 - 8 = 7.)
Задание 9 (с. 11)
30 мин — это половина часа. Акула проплывает 80 км за 1 ч. Тогда за 30 мин она проплывет 40 км (80: 2 = 40).
Задание 5* (с. 10)
(□+□)·5>(□ + □)·0
В окошки можно записывать любые числа. Неравенство будет выполняться всегда, кроме одного случая, если слева будет получаться в произведении нуль. Например: (0 + 0) • 5 = (0 + 0) • 0.
Задание 10 (с. 11)

Сообщение темы и целей урока
Закрепление изученного материала
Задание 1 (с. 10)
23 + 37 + 40 = (23 + 37) + 40 = 60 + 40 = 100
23 + 37 + 40 = 23 + (37 + 40) = 23 + 77 = 100
23 + 37 + 40 = 23 + 40 + 37 = (23 + 40) + 37 = 63 + 37 = 100
23 + 37 + 40 = (20 + 3) + (30 + 7) + 40 = (20 + 30 + 40)+ (3 + 7) = 90 + 10 = 100
Задание 2 (с. 10)
Рассматривается несколько примеров, потом они обобщаются и формулируется закономерность.
а) Возьмем два произвольных числа и найдем их сумму: 12 + 5 = 17. Теперь одно слагаемое (например, первое) увеличим на 7 и снова найдем сумму:
(12+ 7) +5 = 24.
Замечаем, что сумма увеличилась. На сколько? (На 7; 24-17 = 7.)
Закономерность: если слагаемое увеличить на несколько единиц, сумма увеличится на столько же единиц.
б) Сумма сначала увеличится на 15 единиц, потом еще на 7. Всего увеличится на 22 единицы.
в) Сумма увеличится на 20 единиц, затем уменьшится на 3 единицы. Значит, она увеличится на 17 единиц.
Задание 3 (с. 10).
1) Если слагаемое уменьшили на 17 единиц, сумма также уменьшилась на 17 единиц. Чтобы сумма не менялась, нужно второе слагаемое увеличить на 17 единиц.
2) Одно слагаемое увеличили на 20 единиц, сумма также увеличилась на 20 единиц. А по условию нужно, чтобы она уменьшилась на 10 единиц. Значит, нужно уменьшить другое слагаемое: сначала на 20 единиц, а потом еще на 10, всего — на 30 единиц.
Задание 4 (с. 10)
Способ I. Если слагаемое увеличиваем на несколько единиц, сумма увеличивается на столько же единиц. Если слагаемое уменьшаем, сумма уменьшается на столько же единиц.
|
|
|
1) 54 + 18 = 72 — сумма после увеличения;
2) 72 - 7 = 65 — сумма после уменьшения.
Способ II. Последовательное изменение слагаемых увеличит сумму на 11 (18-7 = 11), и она станет равной 65 (54 + 11 = 65).
Задание8 (с. 11)
Ученики записывают только ответы.
Задание 12 (с. 11) - устно
Задание 11 (с. 11)
Способ I.
1) 809 + 31 = 840 (м.);
2) 840-240 = 600 (м.);
Способ II.
1) 809-240 = 569 (м.);
2) 569 + 31 = 600 (м.);
Способ III.
1) 240-31 = 209 (м.);
2)809-209 = 600 (м.).
Подведение итогов урока
Домашнее задание: с. 10 № 6
МАТЕМАТИКА
Тема: Вычитание чисел и величин. Изменение разности в зависимости от изменения ее компонентов
Цели: повторить алгоритм вычитания трехзначных чисел и величин; установить закономерности изменения разности в зависимости от изменения ее компонентов.
Организационный момент
Устный счёт
На доске записаны числа: 15, 16, 17, 18, 19, 29, 30,31.
Увеличьте числа в 6 раз. Уменьшите числа в 6 раз.
Устно решите записанные на доске уравнения.
100-х=23 х:7=12
51:х=17 17-х = 68
Решите задачи:
а) У Кати в альбоме 90 марок, это в 9 раз больше, чем у Тани. Сколько марок у Тани? Измените вопрос так, чтобы задача решалась в 2 действия.
Б) Бочонок с маслом весит 45 кг, пустой бочонок весит 5 кг. Сколько весит масло в 6 таких бочонках?
В) В первом ящике 9 кг огурцов, а во втором — в 2 раза больше. На сколько килограммов огурцов больше во втором ящике, чем в первом?
Г*) Из листа фанеры можно вырезать 5 одинаковых квадратов. Сколько листов фанеры понадобится для того, чтобы вырезать 48 таких квадратов?
Задание 1 (с. 12)
Пример задачи на нахождение остатка.
Учительница принесла в класс 22 тетради и дала каждому из 5 учеников по 4. Сколько тетрадей у нее осталось? (22-4·5 = 2.)
Задание 7 (с. 13)
Задание 6*.
□ 27 9 3 □
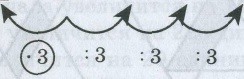
Ответ: 81, 1.
|
|
|


