Главная | Обратная связь | Поможем написать вашу работу!

Методика решения задач оптимизации

При решении любой конкретной задачи оптимизации необходимо выполнить следующую последовательность работ:

1. Содержательно поставить задачу оптимизации. Для этого следует возможно более полно определить (классифицировать) объект оптимизации, т. е. процесс или систему; если систему, то динамическую или статическую; если объект динамический, то непрерывный или дискретный, детерминированный или стохастический.

Необходимо также сформулировать критерий оптимизации, т. е. сформулировать цель оптимизации (что необходимо получить от процесса или системы).

И, наконец, следует достаточно полно определить возможности оптимизации, т. е. сформулировать ограничения на переменные и параметры объекта оптимизации.

2. Полностью определить неизменяемую часть объекта оптимизации, т. е. выделить те характеристики и параметры, которые заданы в виде требований к процессу или системе или существуют объективно. Определить изменяемую часть объекта оптимизации, т. е. выделить характеристики и параметры, изменением которых можно влиять на критерий оптимизации.

3. Выбрать математический метод и построить математическую модель объекта оптимизации, т. е. описать объект оптимизации на языке выбранного математического метода.

4. В соответствии с п. 3 определить вид и характер ограничений, накладываемых в данной задаче на изменяемые характеристики и параметры процесса или системы.

5. В соответствии с пп. 3, 4 сформулировать и формализовать критерий, выбрать метод решения и полностью формально поставить задачу оптимизации.

6. Разработать алгоритм решения задачи оптимизации.

7. Разработать программу решения задачи оптимизации на ЭВМ. Отладить программу. Решить задачу оптимизации на ЭВМ.

Рассмотрим теперь более подробно каждый пункт приведенной

Для нужд практики может быть использована классификация объектов оптимизации, показанная на рис. 15.1.

Содержательная формулировка критерия оптимизации процесса или системы, а также содержательное определение возможностей оптимизации не нуждаются в дополнительном пояснении.

Задача оптимизации отличается от задачи синтеза так же, как часть отличается от целого, т. е. оптимизация является частью синтеза и в этом смысле в известной мере опирается на него. Иными словами, оптимизировать можно то, что уже хотя бы в какой-то мере создано.

Таким образом, если имеются хотя бы «контуры» проектируемого процесса или системы, то всегда можно назвать такие характеристики и параметры этого «контура», которые в данном варианте процесса или системы при оптимизации меняться не будут. Например, если проектируется внешнеэкономическая деятельность предприятия, то таможенные пошлины определяются государством и изменению не подлежат.

Рисунок 15.1 Классификация объектов оптимизации

Выделение изменяемой части объекта оптимизации, по существу, сводится к назначению переменных оптимизации, тех самых характеристик, варьируя значения которых, можно изменять качество процесса или системы, т.е. изменять показатель или критерий оптимизации. Именно эти переменные часто называют оптимизируемыми переменными или параметрами, так как они, принимая некоторые (оптимальные) значения, доставляют экстремум критерию оптимизации.

При выборе и выделении переменных оптимизации следует следить за тем, чтобы их было сравнительно немного и чтобы изменение каждой из них действительно оказывало влияние на критерий оптимизируемого процесса или системы. Естественно, что такое пожелание предполагает хорошее знание особенностей функционирования объекта оптимизации.

Вопрос о построении математической модели объекта оптимизации тесно связан с его идентификацией. Действительно, если объект оптимизации статический, то для его описания применяются математические зависимости типа формул, алгебраических уравнений, логических уравнений или графов. Если объект оптимизации оказался динамическим, то применяют математические конструкции, зависящие в явном или неявном виде от времени, т. е. динамические зависимости. Аналогично можно проследить связь между идентификацией и построением математической модели объекта оптимизации по признакам детерминизма и дискретности.

В математике существует довольно большое количество методов и способов описания статических и динамических объектов. Однако на практике применяется лишь несколько наиболее изученных и отработанных из них. Для построения математических моделей объектов оптимизации в технике связи наиболее часто используются следующие математические зависимости:

— непрерывные функции;

— дискретные (в том числе логические) функции;

— линейные алгебраические уравнения;

— нелинейные алгебраические уравнения;

— трансцендентные уравнения;

— обыкновенные линейные дифференциальные уравнения;

— обыкновенные нелинейные дифференциальные уравнения

— зависимости теории вероятности;

— уравнения в частных производных;

— зависимости теории графов и сетей.

Выбор вида (или видов) математических зависимостей для построения математической модели объекта оптимизации, как уже упоминалось, выше, во многом определяется принадлежностью объекта к тому или иному классу. Обычно этот выбор зависит также и от ряда других факторов, к которым следует отнести следующие: способ задания критерия оптимизации, способ задания ограничении на оптимизируемые параметры объекта оптимизации, наличие или отсутствие адекватных машинных методов и алгоритмов реализации модели объекта оптимизации, сложность применения математических зависимостей того или иного вида для описания объекта оптимизации.

Анализ перечисленных факторов показывает, что выбор математического метода для построения математической модели объекта оптимизации в достаточной степени субъективен. Это обстоятельство исключает возможность выработки единых рекомендаций по выбору математического метода.

Выбор математического аппарата для описания объекта оптимизации накладывает вполне определенные ограничения на все аспекты решения задачи оптимизации, в том числе и на форму, и метод построения и реализации критерия оптимизации. Иными словами, если объект оптимизации описан, например, в метрике (языке) координата, скорость, ускорение, то и критерий оптимизации должен быть сформулирован и описан также в этой метрике.

Однако, кроме языковой стороны, при формализации критерия оптимизации встают еще некоторые вопросы, о которых и пойдет речь ниже. Дело в том, что оценка оптимальности объекта может производиться (и обычно производится) не по одному, а по нескольким частным показателям или критериям.

Принцип формирования обобщенного показателя состоит в том, что один из частных показателей принимается за основной, а остальные учитываются в виде взвешенных слагаемых, обеспечивающих одноименный с основным показателем экстремум критериальной функции или функционала. Указанный принцип формирования обобщенных показателей можно выразить формулой вида

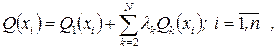
где x_i – параметры оптимизируемого процесса или системы, т. е. суть аргументы функции частных и обобщенного показателей; – число частных показателей оптимальности; – обобщенный показатель; – частные показатели; – основной показатель; – весовые коэффициенты (или функции) частных показателей.

Приведенный способ формирования обобщенного показателя позволяет учитывать ограничения, накладываемые на частные показатели. Эти ограничения могут быть следующего вида:

где – заданное значение , ограничивающее область существования функции .

Пример плоских ограничений показан на рис. 15.2. Здесь область существования функции ограничивается условиям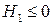и и .

В соответствии с известными принципами формирования обобщенного показателя функция должна удовлетворять следующим требованиям:

1) должна иметь хотя бы одни (желательно и единственный) экстремум в области существования ;

2) внутри области, ограниченной условиями существования суммы функция должна с достаточной степенью точности совпадать с функцией ;

3) вне области, ограниченной этими условиями, функция должна отличаться от функции тем больше, чем больше сумма отличается от ;

Рисунок 15.2 Пример плоских ограничений.

4) для обеспечения возможности автоматической оптимизации непрерывными методами функция должна быть, по крайней мере, кусочно-непрерывной и иметь кусочно-непрерывные первые частные производные (в практических случаях это требование обычно выполняется);

5) функция , равно как и ее составляющие и , должна иметь реальные (с точки зрения машинной реализации) пределы измерения.

Для удовлетворения некоторых из перечисленных выше требований к обобщенному показателю оптимальности может быть применен метод формирующих функций. Так, для удовлетворения требований 1, 2 и 3 можно использовать формирующую функцию вида

или

Обобщенный показатель с применением формирующей функции запишется в виде

При применении формирующей функции обобщенный показатель будет иметь вид

Вообще, для придания функции «экстремальных» свойств можно использовать одновременно различные формирующие функции. Коэффициенты характеризуют «остроту» экстремума, их определяют обычно эмпирическим путем.

«Направление» оптимизации процесса или системы по показателю определяется соотношением весовых коэффициентов . Действительно, при относительном увеличении веса конкретного частного показателя эффективность влияния этого показателя обобщенный показатель увеличивается и оптимизация «делает крен» в сторону этого частного показателя. Если все частные показатели считаются равноценными, то весовые коэффициенты можно определить из следующего выражения:

(15.2)

где – экстремальное значение функции (max или min); или .

Выражение (15.2) отображает требование «равноценности» частных показателей оптимальности в дифференциально малой области экстремума функции .

Машинные методы оптимизации могут быть классифицированы следующим образом:

– основанные на применении классических математических методов;

– основанные на применении принципа максимума;

– основанные на применении линейного и нелинейного дискретного программирования;

– основанные на применении динамического программирования;

– основанные на градиентных методах;

– специальные методы оптимизации;

– методы оптимизации графов и граф-сетей;

– методы оптимизации в условиях неопределенности.

Выбор класса машинных методов оптимизации для решения конкретной задачи зависит в основном от следующих факторов, от принадлежности объекта оптимизации к тому или иному классу, от способа задания критерия оптимизации, от результатов композиции и декомпозиции объекта оптимизации, от личных склонностей и уровня подготовки лица, принимающего решение.

Анализ перечисленных факторов показывает, что выбор машинного метода оптимизации хотя и в меньшей степени, чем выбор математической модели объекта оптимизации, все же остается весьма субъективным. Это обстоятельство в значительной степени затрудняет возможность выработки единых рекомендаций по выбору машинного метода оптимизации. Однако основанные на опыте частные рекомендации в значительной мере могут облегчить работу инженера при решении конкретных задач оптимизации

Итак, если объектом оптимизации оказался некоторый объект и для его описания применена непрерывная на некотором участке функция критерия, то в качестве машинного метода оптимизации такого объекта может быть рекомендован один из методов, основанных на классической математике, один из градиентных методов или один из специальных методов.

Если в качестве объекта оптимизации выступает некоторая система (или процесс) управления, описываемая дифференциальными уравнениями, а критериальная функция представлена в виде интеграла от функции фазовых координат системы, то в качестве машинных методов оптимизации здесь может быть рекомендована целая серия процедур от классического вариационного исчисления до принципа максимума и динамического программирования включительно.

Задачи оптимизации, в которых в качестве объекта оптимизации выступают сети связи, а в качестве критериев оптимальности применяются функции или функционалы, связанные с пропускными способностями, могут успешно решаться с помощью машинных методов оптимизации сетей или машинных вероятностных методов (марковские методы, методы теории игр п др.).

Проблему оптимизации в смысле разработки машинного алгоритма целесообразно рассматривать в двух направлениях: направлении, когда объект оптимизации представляется полностью своей критериальной функцией или функционалом, и направлении, когда объект оптимизации и его критериальная функция или функционал представляются самостоятельно и раздельно.

Рассмотрим вначале первое направление. Случай, когда объект оптимизации представлен полностью своей критериальной функцией или функционалом, хотя и является простейшим, встречается весьма часто. На самом деле, предположим, что при проектировании того или иного объекта ЛПР удастся выразить некоторое качество объекта через его основные параметры , часть из которых (или все) можно варьировать в определенных пределах. В этом случае инженер оказывается в таких условиях, когда не поставить задачу оптимизации объекта по данному качеству за счет выбора наилучших значений параметров , просто невозможно

Но тогда получается как раз тот случай, когда необходимо найти экстремум (максимум пли минимум в зависимости от физической сущности задачи) функции или функционала по переменным , т. е. имеет место случай полного выражения объекта оптимизации через функцию или функционал критерия оптимизации.

Проблема разработки алгоритма оптимизации и этом случае сводится к выбору или разработке программы нахождения экстремума функции по нескольким переменным. Если функция непрерывна или кусочно-непрерывна, то могут быть применены машинные алгоритмы, основанные на классической математике, градиентные или специальные машинные алгоритмы (случайный поиск, или алгоритм обхода узловых точек). Если функция Q дискретная, то могут быть применены алгоритмы целочисленного или динамического программирования.

Гораздо более сложным оказывается путь построения алгоритма оптимизации, когда объект оптимизации и его критериальная функция (или функционал) представлены самостоятельно. В этом случае процедура оптимизации оказывается составной и сводится к следующему:

1) первоначальное задание некоторого состояния объекта и вычисление начального значения критериальной функции (или функционала);

2) изменение значений оптимизируемых параметров и вычисление соответствующих изменений состояния объекта и критериальной функции (функционала);

3) определение оптимальных (в смысле выбранного критерия) направлений изменения оптимизируемых параметров, вычисление их новых значений и установка этих значении на модели объекта;

4) контроль на окончание оптимизации;

5) повторение пп. 2–4 до тех пор, пока по п. 4 не произойдет останов.

Более наглядно приведенный алгоритм оптимизации представлен на рис. 15.3.

Рис. 15.3 Алгоритм оптимизации объекта

Рассмотрение структурной схемы алгоритма оптимизации показывает, что для решения сложных задач оптимизации приходится разрабатывать не только алгоритм собственно оптимизации, но и алгоритмы модели оптимизируемого объекта и алгоритм вычисления критериальной функции или функционала.

Г Л А В А 16
Общая задача оптимизации экономических систем

Общая задача оптимизации

Будем рассматривать общую задачу оптимизации, сформулированную в следующей стандартной форме. Рассмотрим задачу максимизации:

, (16.1)

, (16.2)

где – некоторое подмножество множества индексов ,

– целевая функция,

– n -мерный вектор переменных задачи.

Ограничения (16.1) – функциональные ограничения; ограничения (16.2) – прямые.

Функции предполагаются непрерывными функциями из классов С¹ или С² в зависимости от потребностей, если не оговорено противное.

Удобно иметь все неравенства одного знака. Если же встретятся неравенства вида , всегда можно, обозначив , свести систему к стандартной форме. Естественно, что знак неравенства в стандартной форме произволен. Приведенный выше выбор знака для задачи на максимум (и обратные знаки в задаче на минимум) естествен во многих экономических задачах и в задачах линейного программирования. Обычно в задачах, использующих методы Куна и Таккера, неравенства записываются по-другому. Однако мы сохраним приведенное выше соглашение о знаке для всех задач.

Функциональное ограничение всегда можно представить в виде неравенств. Для этого ограничение вида представляют в виде пары условий . В случае, когда все ограничения – равенства, целесообразно оставить эту форму.

Прямые ограничения (16.2), которых может и не быть (S может быть пустым множеством), всегда записывают, как условия на неотрицательность. Такой знак прямых ограничений естественно сохранить и в задаче на минимум, в которой знаки неравенств в функциональных ограничениях меняются на противоположные. Все прямые ограничения можно представить в таком виде, обозначая ,если в начальных условиях , или ,если .

Чтобы обеспечить замкнутость допустимого множества, предполагается, что все неравенства записаны как нестрогие.

Задача на оптимум, вообще говоря, не всегда имеет решение. Задача при условии, что , имеет неограниченное допустимое множество и не имеет решений: для любого х можно найти другой допустимый вектор, дающий большее значение целевой функции. Тем не менее, можно выделить широкий класс задач, для которых гарантируется существование оптимума.

Теорема Вейерштрасса: непрерывная функция, определенная на непустом замкнутом ограниченном множестве, достигает максимума (минимума), по крайней мере, в одной точке этого множества.

Поскольку обычно целевая функция берется непрерывной, а допустимое множество замкнутым, то ограниченность допустимого множества – единственное необеспеченное условие.

Во многих случаях допустимое множество будет ограничено, однако это не будет очевидным без соответствующего исследования. Будет установлено, что теорема Вейрштрасса дает достаточныеусловия оптимума. Задачи, в которых не выполняются условия теоремы, могут иметь оптимум[4].

Задача на оптимум может, конечно, быть и тривиальной. Функция при ( – скаляр) имеет и максимум, и минимум, равный .

16.2 Общий принцип решения

Оптимальная точка должна лежать в допустимом множестве. Это либо внутренняя, либо граничная точка множества.

Пусть оптимальная точка является внутренней. Тогда существует окрестность, содержащая эту точку и целиком лежащая в допустимом множестве, причем рассматриваемая точка оптимальна относительно точек этой окрестности. Такая точка должна удовлетворять обычным требованиям к безусловному оптимуму, то есть она должна быть критической точкой f ( для всех f)[5].

Пусть теперь оптимальная точка лежит на границе. Тогда в любой ее окрестности имеются точки как принадлежащие, так и не принадлежащие допустимому множеству. Поэтому, вообще говоря, нельзя сказать, что эта точка является оптимальной относительно точек своей окрестности. Граничная оптимальная точка не обязательно должна быть критической точкой f.

Таким образом, имеем общий принцип решения: решение общей задачи на оптимум (max или min 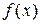при , принадлежащих замкнутому допустимому множеству ), если оно существует, является либо критической точкой функции 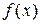, либо граничной точкой множества , либо и тем и другим одновременно.

Мы выделили два типа оптимальных точек – внутреннийи граничныйоптимумы. Это показано на рис. 16.1 а и б.На обоих рисунках эллиптические кривые представляют собой линии (или в общем случае поверхности) уровня целевой функции, а выделенная область – это допустимое множество. Оптимальная точка А является внутренним оптимумом на рис.16.1 аи граничным на рис. 16.1 б.

Рисунок 16.1 Внутренний (а) и граничный (б) оптимумы

В принципе, задача оптимизации может быть решена следующим образом. Находятся критические точки 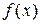,затем вычисляются значения 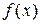вдоль границы, и, наконец, сравнивая полученные при этом значения целевой функции, выбираются точки, дающие максимум или минимум функции 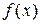.На практике этот подход к решению задачи оказывается слишком трудоемким.

Если 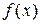не является всюду дифференцируемой, то вместе с критическими и граничными точками необходимо исследовать и точки, в которых 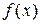недифференцируема.

16.3 Принцип Парето

Принцип Парето позволяет сократить множество исходных вариантов, то есть исключить те варианты решений, которые заведомо будут неудовлетворительными.

Предположим, что мы сделали некоторый выбор. Обозначим его через и предположим, что существует некоторый другой выбор такой, что для всех критериев имеют место неравенства

, (16.3)

причем хотя бы одно из неравенств – строгое.

Очевидно, что выбор предпочтительнее . Поэтому все векторы , удовлетворяющие (16.3), следует сразу исключить из рассмотрения. Имеет смысл заниматься сопоставлением, подвергать анализу только те векторы , для которых не существует такого, что для всех критериев удовлетворяется неравенство (16.3). Множество всех таких значений называют множеством Парето, а вектор называют неулучшаемым вектором результатов (вектором Парето), если из для любого следует .

Предположим, что цели субъекта определяются двумя однозначными функциями:

Тогда каждому допустимому значению переменной отвечает одна точка на плоскости (рис. 16.2), и равенства

определяют параметрическое задание некоторой кривой в этой плоскости. Но к множеству Парето можно отнести далеко не всю кривую. Так, участок , очевидно, не принадлежит множеству Парето, поскольку вместе с ростом происходит рост . Таким образом, на этом участке изменению переменной отвечает одновременное увеличение обеих целевых функций, и, следовательно, такие варианты решений должны быть сразу исключены из дальнейшего рассмотрения.

Рисунок 16.2 Парето-предпочтение альтернатив

Из тех же соображений должен быть исключен участок , поскольку для каждой его точки найдется точка, принадлежащая участку , в которой значения обеих функций и больше, чем в точке . Значит, претендовать на принадлежность к множеству Парето могут только участки и , причем точка также должна быть исключена.

Таким образом, принцип Парето заключается в том, что выбирать в качестве решений следует только тот вектор , который принадлежит множеству Парето. Принцип Парето не выделяет единственного решения, он только сужает множество альтернатив. Окончательный выбор остается за лицом, принимающим решение. Но исследователь, построив множество Парето, естественно, облегчает процедуру выбора решения.

Принцип Парето играет очень важную роль в автоматизации проектирования. Предположим, например, что речь идет о проектировании водного комплекса. В результате создания этого комплекса появится возможность обеспечить водой несколько крупных промышленных и сельскохозяйственных объектов и тем самым повысить их эффективность. Но возникнет целый ряд отрицательных явлений. Большая площадь водохранилища, которая необходима для регулярной работы комплекса, приведет к большим потерям воды в результате испарения. Кроме этого, уменьшение количества воды в речной системе ухудшит условия рыболовства и судоходства, а строительство промышленных комплексов увеличит объем загрязнений и ухудшит качество воды, поступающей на поля. Одним словом, ситуация оказывается многокритериальной. Цели проектировщика могут быть записаны в виде:

Проектировщик сталкивается с необходимостью поиска компромисса, одним из путей которого является построение множества Парето, изучение которого дает большой объем информации. Лицо, принимающее решение, сможет увидеть, во сколько обойдется увеличение одного из показателей, как это скажется на остальных показателях, значения которых непременно ухудшатся. Как правило, это множество имеет очень сложную природу.

Помимо критериев , часто существует еще один общий критерий . Иногда он может быть записан в явном виде. Таким критерием является стоимость проекта. Значит, для решения задачи достаточно определить вектор : при , где – множество Парето для функций на множестве допустимых векторов . Так, для водного комплекса множество определяется распределением воды по объектам , при котором ее количество не превосходит притока .

Приближенное построение множества Парето относится к числу очень важных и очень трудных задач численного анализа. Рассмотрим простейший случай двух критериев.

Пусть речь идет о задаче

Каждой точке соотношения

ставят в соответствие некоторую точку в плоскости критериев (рис. 16.3). Эти соотношения определяют отображение множества на .

Рисунок 16.3 Приближенное построение множества Парето

Множество носит название множества достижимости или множества предельных возможностей. Изучение структуры этого множества может оказаться весьма полезным при исследовании задач проектирования и планирования. Множество Парето представляет собой лишь часть границы множества достижимости. На рис. 16.3 множеством Парето будет дуга .

Приближенное построение множества Парето сводится к последовательному решению ряда задач математического программирования. Опишем одну из возможных схем расчета. Зафиксируем некоторые значения критериев и :

Значения 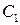и следует выбрать так, чтобы они принадлежали множеству достижимости.

Теперь решаем две оптимизационные задачи.

Решив эти задачи, мы определим точки и (рис. 16.4). Проведя через них прямую 1, мы получим простейшую аппроксимацию множества Парето.

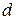Для уточнения аппроксимации, решив задачи 3 и 4, мы находим еще две точки и , которые принадлежат этому множеству:

Рисунок 16.4 Краевые задачи при построении множества Парето

Значения 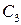и 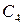снова должны принадлежать множеству достижимости. Через точки мы проведем ломаную 2, которая и будет следующим приближением. Очень часто подобной информации о структуре множества Парето уже бывает достаточно для решения практических задач. Описанный способ можно распространить и на случай большего числа критериев.