 |
Седловые точки и двойственность
|
|
|
|
Рассмотренные выше оптимальные условия для общей задачи максимизации обычно называются условиями Куна-Таккера.
Обычно они выражаются в терминах функции Лагранжа:
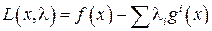
изаписываются в векторной форме при помощи введенных ранее обозначений. В этих обозначениях условия оптимальности имеют вид:
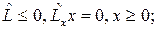
В первоначальной формулировке Куна и Таккера и в большинстве изложений теории Куна-Таккера ограничения приводятся в форме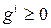 
, а функция Лагранжа – в виде 
.Противоположные знаки в ограничениях и перед 
взаимно уравновешивают друг друга. Поэтому форма условий оптимальности не меняется.
Мы уже заметили, что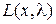 
– функция от двух наборов переменных – имеет в оптимальной точке максимум по х и минимум по . Точка, в которой функция достигает максимума по одним переменным и минимума по другим, называется седловой точкой. Возникновение этого термина объясняется видом графика функции Лагранжа в трехмерном пространстве.
Поэтому решение общей задачи оптимизации может рассматриваться как нахождение седловой точки функции Лагранжа или точки, максиминимизирующейили минимаксимизирующейфункцию Лагранжа. Последняя терминология следует из того, что мы находим максимум по х и минимум по . Далее будет показано, что если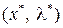 
– оптимальная точка L,то
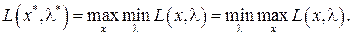
Теперь мы можем строго установить связь между множителями Лагранжа и двойственными переменными задачи линейного программирования.
Рассмотрим стандартную задачу линейного программирования и двойственную к ней
Функция Лагранжа для прямой задачи имеет вид
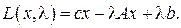
Имеем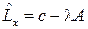 
и 
. Условия Куна-Таккера записываются в виде:
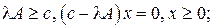
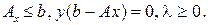
Пусть 
.Тогда условия Куна-Таккера будут представлять собой ограничения и условия равновесия для прямой и двойственной задач. Если мы построим функцию Лагранжа для двойственной задачи, получим, что оптимальные значения обеих функций Лагранжа равны между собой: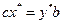 
.Это равенство соответствует теореме двойственности линейного программирования.
|
|
|
Таким образом, множители Лагранжа в общей задаче оптимизации играют роль двойственных переменных в линейном программировании и сводятся к ним, если общая задача оптимизации линейна.
Поэтому в экономических задачах множители Лагранжа можно интерпретировать так же, как и двойственные переменные (обычно как неявные или условные оценки).
Очевидно, что условия Куна-Таккера являются обобщением условий оптимальности каждого частного типа задач оптимизации. Теоретически, можно было бы исходить из этих более общих условий при рассмотрении частных случаев – линейного программирования и строгих классических задач на условный оптимум.
Двойственные переменные
Рассмотрим общую задачу максимизации, для которой известно решение х*. Необходимо найти оптимальные значения двойственных переменных . Такой тип задач играет важную роль в экономическом анализе, где предполагается, что отдельные составляющие экономической системы (обычно фирма или потребитель) уже определили координаты своего оптимума тем или иным способом (возможно, ошибочно). Интересно знать, какова природа двойственных переменных, связанных с оптимумом и обычно рассматриваемых как некоторые условные оценки.
Поскольку оптимальное значение х* задано, величины 
, 
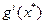и их производные могут рассматриваться как константы. Для упрощения записи обозначим матрицу из 
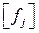через 
,вектор 
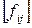– через c,а вектор 
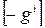– через b. А – матрица порядка 
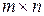, с – вектор-столбец порядка п,а b – вектор-строка порядка т.
Если рассматривается задача в строго классической форме, где все ограничения – равенства и отсутствуют требования неотрицательности х (но не ), условия оптимальности по х запишутся в виде
|
|
|
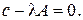
Приведенное соотношение представляет собой систему уравнений относительно .В этой системе n уравнений и только т переменных . Однако, природа оптимального решения гарантирует, что только т уравнений линейно независимы. В качестве базиса АB можно взять любые m строк матрицы А. Обозначим соответствующие элементы с через сB. Тогда определяется из системы
В общей задаче максимизации условия оптимальности представляют собой неравенства. Взяв необходимую для определения часть условий Куна-Таккера, получим
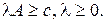
Приведенные неравенства похожи на ограничения в задаче линейного программирования. Подберем подходящую целевую функцию. В нашем случае 
,которая достигает минимума по в точке 
,линейна относительно скоэффициентами (
).Величина является константой и при оптимизации может быть отброшена. Следовательно, минимизация 
по эквивалентна минимизации b,где b определено раньше.
Таким образом, мы установили, что в общей задаче максимизации оптимальные значения при заданном х* определяются из следующей задачи линейного программирования:
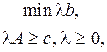
где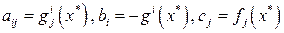 
.
Ранее было показано, что в строгом классическом случае множители Лагранжа удовлетворяют соотношениям
,
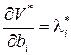где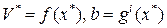 
.Это привело к интерпретации оптимальной величины i ‑го множителя как предельного значения ослабления i -гo ограничения.
Можно ли в общем случае дать множителям ту же интерпретацию? Оказывается, можно, но с большими изменениями.
Если, как и в классическом случае, положить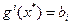 
,то нетрудно установить следующее утверждение. Если 
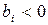, то есть ограничение неэффективно, то малое ослабление не влияет на оптимальные значения х и поэтому не влияет и на . Следовательно, будем иметь 
,если 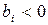. Однако, из условий Куна-Таккера следует, что 
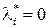, если 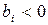. Таким образом, при неэффективности ограничений в общем случае справедливы те же соотношения, что и в классическом случае.
При малых вариациях в окрестности оптимума неэффективные ограничения остаются неэффективными и могут быть отброшены. Следовательно, можно рассматривать задачу только с ограничениями-равенствами. Если же все прямые ограничения на х неэффективны, то анализ проводится точно так же, как в классическом случае.
|
|
|
Именно требование неотрицательности х,а не неравенства в функциональных ограничениях, заставляет беспокоиться. Игнорируя неэффективные функциональные ограничения и проводя анализ, аналогичный анализу в классическом случае, получаем соотношение
где S – множество индексов эффективных ограничений, а все производные взяты в оптимальной точке.
В классическом случае из-за условий оптимальности выражение в скобках обращается в нуль, и равенство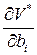 
и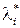 
установлено. В рассматриваемом случае то же самое выполняется, если х* строго положительный вектор.
Если же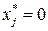 
для некоторого j, выражение в скобках может быть отрицательным, и условия Куна-Таккера выполнябтся. Рассмотрим положительное изменение bi,. Из требования неотрицательности х следует, что 
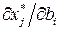неотрицательно, если .
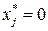Следовательно,
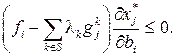
Поэтому в общем случае имеем
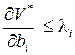либо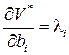 
, либо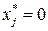
для некоторого j;
если 
.
Экономическая интерпретация совершенно ясна. Множитель 
представляет собой предельную величину изменения i -го ограничения (0, если ограничение неэффективно) при условии, что прямые ограничения неэффективны в х*. Если же существует эффективное прямое ограничение в х*,оно ограничивает возможность изменения х* и стремится уменьшить величину ослабления функционального ограничения.
Требование неотрицательности не усложняет ситуацию. Ослабление ограничений не может уменьшить оптимальное значение V,так что 
неотрицательно.
Теорема о минимаксе
В задаче, имеющей локальный условный максимум, функция Лагранжа удовлетворяет условию
,
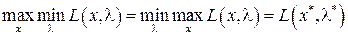где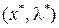 
– седловая точка .
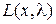В этом пункте будет показано, что minimax 
= maximin тогда и только тогда, когда имеет седловую точку. Затем будут приведены условия, гарантирующие существование седловой точки у функции .
Рассмотрим непрерывную функцию ,определенную на множествах X и Y. Можно утверждать следующее:
Теорема I: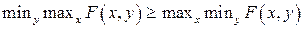 
. Равенство выполняется тогда и только тогда, когда F (х, у) имеет седловую точку (х*, у*). В этом случае 
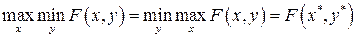[13].
Прежде всего, заметим, что по определению 
для всех х и любого у независимо от того, имеет седловую точку или нет. Тогда
|
|
|
для всех х. Таким образом, первая часть теоремы доказана. Это предложение (minimax F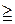 
minimax F)может рассматриваться как основная лемма. Аналогия этой леммы с основной леммой линейного программирования очевидна.
Предположим, что (х*, у*) – седловая точка функции .Обозначим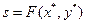 
.По определению седловой точки имеем 
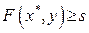для всех у;следовательно,
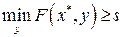
и
.
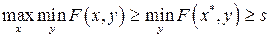Аналогично, исходя из неравенства 
для всех х,получаем
.
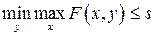Отсюда
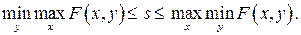
Сравнивая полученное соотношение с неравенством, составляющим содержание основной леммы, получаем
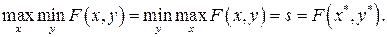
Следовательно, существования седловой точки достаточно для выполнения утверждения теоремы.
Докажем необходимость. Выберем х* таким образом, что
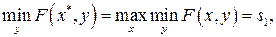
а у* – так,что
Поскольку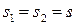 
,то
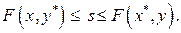
Следовательно, 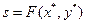определяет седловую точку. Доказательство теоремы завершено.
Теперь можно доказать следующую теорему существования.
Теорема II: пусть множества X и Y выпуклы. Кроме того, пусть функция выпукла по у для всех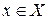 
и вогнута по х для всех 
. Тогда имеет седловую точку.
Определим следующие множества:
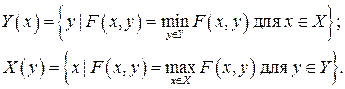
Поскольку выпукла по у и вогнута по х,множества Y (х)и X (у) – выпуклые. Из свойств непрерывности оптимальных решений следует, что отображения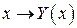 
и 
полунепрерывны сверху. Следовательно, отображение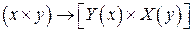 
является полунепрерывным сверху 
в собственное компактное выпуклое подмножество. Условия теоремы Какутани о неподвижной точке выполнены. Из теоремы следует, что существуют векторы х* и у*,такие, что 
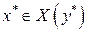,а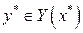 
.То есть х* максимизирует 
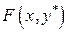,а у* минимизирует 
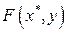,так что
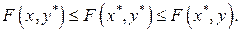
Что и требовалось доказать.
|
|
|
