 |
Постановка задач многокритериальной и теоретико-игровой оптимизации
|
|
|
|
Многокритериальная оптимизация имеет место как в статических, так и динамических задачах управления. Общая модель статической задачи многокритериальной оптимизации:
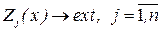; (18.1)
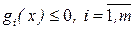; (18.2)
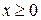. (18.3)
Здесь 
- вектор критериев задачи (18.1) – (18.3). условия (18.2), (18.3) определяют область допустимых решений задачи Х.
Общая модель динамической задачи многокритериальной оптимизации:
; (18.4)
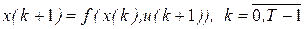; (18.5)
; (18.6)
Здесь - вектор критериев задачи (18.4) – (18.7). Условие (18.5) определяет уравнение движения системы. Условие (18.6) задает ограничения, накладываемые на параметры состояния системы 
и параметры управления системы 
. Выражение (18.7) определяет граничное условие задачи.
При решении многокритериальных задач управления возникает ряд специфических проблем, носящих не формальный (т.е. вычислительный), а концептуальный характер. Из них главная – выбор принципа оптимальности, определяющего свойства оптимального решения и дающего ответ на главный вопрос – в каком смысле оптимальное решение лучше всех других.
В задачах многокритериальной (векторной) оптимизации имеется противоречие между некоторыми из критериев. Это противоречие является нестрогим, так как оно определяется лицом, принимающим решение (ЛПР). В силу этого область допустимых решений 
распределяется на две непересекающиеся части: область согласия 
и область компромисс 
. В области согласия противоречия между критериями нет и качество решения может быть улучшено одновременно по всем критериям или во всяком случае без ухудшения уровня любого из критериев. В области компромисса есть противоречие между некоторыми критериями, т.е. улучшение качества решения по одним критериям ухудшает качество решения по другим.
|
|
|
Очевидно, что оптимальное решение может принадлежать только области компромисса, т.е. 
, так как в области согласия решение может и должно быть улучшено по всем критериям. Выделение области компромисса обычно является первым этапом решения многокритериальной задачи. Графически это представлено на рис. 18.1. Пусть область Z определяет множество значений векторного критерия 
. При условии, что ищется максимум обоих критериев Z1 и Z2, область компромисса определяется стороной АВ, так как на ней увеличение одного критерия приводит к уменьшению другого критерия.
Рис. 18.1. Область значений критериев
Множество компромиссных планов принято называть оптимальным по Парето. Содержательно оптимальным по Парето является такой допустимый план, для которого не существует другого плана, который по всем критериям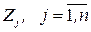 
был бы лучше данного плана. С математической точки зрения можно сказать, что 
есть точка Парето, если
(18.8)
Поиск оптимальных решений в области компромисса связан с определением основных особенностей многокритериальной задачи и выбором алгоритма решения. Основные особенности многокритериальной задачи определяются заданной информацией о сравнимости критериев, о сравнимости количественных значений критерия, дополнительных свойствах оптимального решения или требований к нему. Выбор алгоритма решения определяется в основном двумя взаимосвязанными схемами определения оптимального компромисса. Первая схема связана с нахождением функционала 
, монотонно зависящего от функций 
, максимуму которого соответствует решение многокритериальной задачи. Вторая схема связана с определением частичного упорядочения (предпочтения) на множестве решений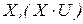 
.
Теоретико-игровая оптимизация также имеет место как в статических, так и динамических задачах управления. Под теоретико-игровой моделью понимается формализованное представление поведения нескольких лиц (игроков), принимающих решение. Противоречие интересов лиц (игроков), принимающих решение, может быть выражено в конфликтной форме.
|
|
|
Пусть I - конечное множество игроков 
, где n - число игроков. Поставим в соответствие каждому игроку 
некоторое множество стратегий 
поведения (решений). Множество 
называется множеством ситуаций игры. Пусть на множестве 
определена функция 
, принимающая вещественные значения и называемая функцией выигрыша. Тогда упорядоченная тройка множеств
(18.9)
или
(18.10)
определяет игру в нормальной форме. Содержание игры в нормальной форме состоит в том, что каждый из игроков, выбирая свою стратегию, участвует в создании ситуации 
или 
. В зависимости от ситуации каждый i -тый игрок получает выигрыш .
Естественно считать, что целью каждого игрока является достижение максимального значения своей функции выигрыша. Однако так как выигрыш игрока зависит от ситуации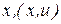 
, а сам игрок может влиять на образование ситуации лишь частично, то вопрос о том, как игрок может осуществить свою цель, оказывается нетривиальным. Остановимся на этом вопросе более подробно. Пусть 
- ситуация игры. Обозначим через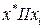 
ситуацию, получаемую из 
заменой в ней стратегии 
игрока i на стратегию 
. В соответствии с определением по Нэшу ситуация 
называется благоприятной для игрока i, если для любого 
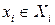
. (18.11)
Ситуация, благоприятная для каждого игрока, называется ситуацией равновесия игры. Понятие ситуации равновесия является центральным в теории игр. Решение игры связано с нахождением ситуации равновесия. Методы решения игры зависят от классификации игры. Можно отметить следующие основные признаки, по которым осуществляется классификация игр: по количеству игроков, количеству стратегий, характеру взаимоотношений, характеру выигрышей, виду функции выигрыша, количеству ходов, состоянию информации.
В зависимости от количества игроков определяют игры одного игрока, двух игроков, п игроков. По количеству стратегий игры делятся на конечные и бесконечные. Если в игре каждый из игроков имеет конечное число возможных стратегий, то игра называется конечной. Если хотя бы один из игроков имеет бесконечное число стратегий, то такая игра называется бесконечной. По характеру взаимоотношений игры делятся на бескоалиционные, кооперативные и коалиционные. Бескоалиционными называются игры, в которых игроки не имеют права вступать в соглашения, образовывать коалиции. Коалиционной игрой называется игра, в которой игроки могут вступать в соглашения, образовывать коалиции. В кооперативной игре коалиции определены наперед. По характеру выигрыша игры делятся на игры с нулевой суммой и игры с ненулевой суммой. Игра с нулевой суммой будет тогда, когда сумма выигрыша всех игроков равна нулю. В частности, игра двух игроков с нулевой суммой называется антагонистической, так как цели игроков в ней прямо противоположны, т.е. выигрыш одного игрока происходит за счет проигрыша другого. По виду функций выигрыша игры делятся на матричные, сепарабельные и др. По количеству шагов игры делятся на одношаговые и многошаговые. В свою очередь многошаговые игры делятся на позиционные, стохастические, дифференциальные и др. В позиционных играх участвуют несколько игроков, каждый из которых может последовательно во времени делать несколько ходов. Выигрыши определяются в зависимости от исходов игры (применяемых стратегий). Такие игры с помощью определенных способов сводятся к матричным играм и могут решаться присущими им методами. Если в игре производятся ходы, приводящие к выбору определенных позиций, причем известна вероятность возврата на предыдущую позицию, то такая игра называется стохастической. Если в многошаговой игре допускается делать ходы непрерывно и подчинять поведение игроков некоторым условиям, описываемым дифференциальными уравнениями, то такие игры называются дифференциальными. В зависимости от состояния информации различают игры с полной и неполной информацией. Если на каждом шаге игры известно, какие выборы были сделаны игроками раньше, то это игра с полной информацией. Если в игре не все известно о предыдущих выборах, то это игра с неполной информацией.
|
|
|
|
|
|
|
|
|
