Условия глобального оптимума в классической задаче на условный оптимум

В классической задаче на условный оптимум все т ограничений являются равенствами, и 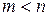.Вообще говоря, эту систему уравнений можно свести к одному уравнению от независимых переменных. Единственный вид уравнения, решения которого образуют выпуклое множество, – линейное уравнение. Так что область определения целевой функции является выпуклым множеством только в том случае, когда 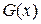линейна. Для линейности 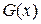достаточно, чтобы все 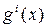были линейны. Это условие не является необходимым, поскольку нелинейные поверхности могут определять линейное пересечение.

Только в случае линейного ограничения удовлетворяются условия глобального оптимума. Этот случай охватывает большой класс простых экономических моделей.

В задаче потребительского выбора, сформулированной в предыдущем пункте, условия глобального оптимума не выполняются, поскольку допустимое множество, определяемое уравнением ,не выпукло. Известно, что в этом случае могут возникнуть те же ситуации, что и в задаче максимизации при выполнении линейного бюджетного ограничения.

Поскольку эта задача удовлетворяет условию глобального оптимума, можно надеяться, что обращенная задача (задача минимизации рх при условии )также должна иметь глобальный оптимум.

Действительно, в задаче, аналогичной задаче потребительского выбора, можно выполнить условия глобального оптимума, если сделать ограничения неравенствами. Множество, определяемое соотношением 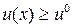,выпукло. Но полученная задача уже не является задачей классического типа. Хотя, как мы увидим в следующей главе, в этом случае решение задачи при ограничениях-неравенствах будет совпадать с решением классической задачи, если обеспечено выполнение условий глобального оптимума. Заметим, что классические условия второго порядка гарантируют существование локального максимума или минимума при некоторых оговорках. При этих оговорках, однако, более общие условия следующей главы не выполняются.

Классический метод решения задач на условный оптимум предполагает равенства в функциональных ограничениях и отсутствие прямых ограничений (обычно это ограничения на неотрицательность переменных). Этот метод широко используется в экономическом анализе. Однако большинство экономических задач в явном или неявном виде содержат особенности, которые не позволяют анализировать их классическими методами. Почти всегда неявно предполагается неотрицательность, по крайней мере, некоторых переменных. Функциональные ограничения точнее описываются неравенствами, чем равенствами. Традиционный экономический анализ основывается на убежденности (часто обоснованной) в том, что функциональные ограничения всегда эффективны, а прямые – несущественны в окрестности оптимума. Часто возникают осложнения из-за того, что неявные ограничения упускаются из рассмотрения и не формализуются. Экономисты развивают модели все возрастающей сложности. Поэтому область использования немодифицированного классического метода решения задач на условный оптимум все более и более ограничивается.

Рассмотрим следующий простой пример. Пусть функция полезности потребителя, зависящая от двух переменных (объемов продуктов и ), задается в виде .Доход потребителя равен единице. Кроме того, задан вектор цен на продукты (15.1). Требуется найти равновесное потребление. Сформулированная задача оптимизации может быть записана в следующем виде:

Решим эту задачу, используя традиционные методы. Получим оптимальные значения переменных 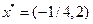и оптимальный уровень полезности 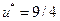. Мы пришли к отрицательному значению одной переменной, несмотря на то, что принятый вид функции полезности вполне естественный.

Получив отрицательное значение составляющей решения, экономист отверг бы его, сказав: «Я забыл вас предупредить, что объемы продуктов не могут быть отрицательными». При формальном подходе к задаче не всегда очевидно, что ограничения на неотрицательность могут оказаться существенными.

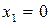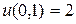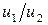Пусть теперь . Это ближайшая точка, куда можно прийти из оптимальной точки, найденной без учета ограничения на неотрицательность. Тогда и , то есть .В точке (0,1) отношение [11] равно 2, a 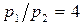. Как видим, в этой точке классическое условие не выполняется. Однако непосредственное вычисление показывает, что при условии неотрицательности переменных точка (0,1) оптимальна.

Аналогичная ситуация возникает в простой модели экономической системы, в которой обращаются два продукта и два фактора. При этом предполагается, что запасы факторов заданы. Рассмотрим производственные функции, у которых кривые постоянства объемов выпусков пересекают оси (подобно кривым безразличия функции полезности, приведенной выше). Из того, что классические условия для оптимального производства выполняются – множества постоянных объемов касаются – следует, что один из факторов имеется в отрицательном количестве. Производственные функции, приводящие к подобной ситуации, возможны, поэтому необходимо уметь обращаться с такими ситуациями. Производство с одним видом капитала или с одним видом труда кажется весьма частным случаем простой модели, в то время как производство с нулевым количеством одного или более видов труда или капитала в сложной модели представляет собой обычную ситуацию.

Простейшим расширением классических задач на условный оптимум являются задачи, в которых все или некоторые переменные подчинены прямым ограничениям. Такими ограничениями чаще всего являются ограничения на неотрицательность. Рассмотрим задачу максимизации вида

Определим функцию 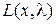обычным образом. Возможны три ситуации:

а) функция 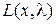имеет регулярный[12] локальный максимум в критической точке 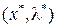при 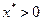, и задача удовлетворяет условиям сильного глобального оптимума (допустимое множество выпукло, функция 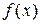вогнута, и либо выпуклость, либо вогнутость строгая);

б) функция 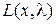имеет регулярный локальный максимум в критической точке 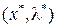при 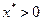, но условия глобального оптимума не выполняются;

в) функция 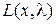не имеет критической точки при 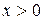, которая являлась бы локальным максимумом.

В первом случае ограничения на неотрицательность неэффективны в окрестности глобального оптимума, и ими можно пренебречь. Этот случай встречается в традиционном экономическом анализе.

В третьем случае глобальный оптимум должендостигаться в точке, в которой какое-либо ограничение на неотрицательность существенно.

Во втором случае оптимум можетдостигаться в такой точке. Обычно это необходимо проверить.

Рассмотрим свойства функци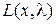й и 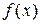в точке, в которой , по крайней мере, для одного индекса k. Поскольку функциональные ограничения пока еще представляют собой равенства, максимумы 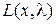и 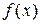достигаются в одной и той же точке х^*. Кроме того, из 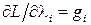следует, что . Таким образом, некоторые из условий первого порядка для максимума L по-прежнему выполняются.

Какие из оставшихся условий первого порядка будут еще выполняться? При случайном сочетании параметров условий задачи они еще могут выполняться. Однако в общем случае эти условия не выполняются. Какими же условиями они заменяются?

Разделим множество индексов компонент вектора х на две группы. Пусть ,если , и , если 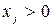. Тогда интересующий нас вопрос можно рассматривать следующим образом.

Пусть . При этом малые вариации x_j возможны как в одну, так и в другую сторону. Поэтому х не может быть оптимальным, если .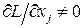

Пусть теперь . Тогда малые вариации возможны только в сторону увеличения .Поэтому, если , х не может быть оптимальным. Иначе можно было бы увеличить L при малом возрастании х. Однако малые уменьшения х не допустимы, поэтому нельзя исключать из рассмотрения точку х,если в ней .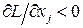

Подведем итоги всего вышесказанного.

Оптимальная точка х^* задачи max 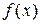при условии, что 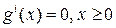, удовлетворяет условиям:

Если же рассматривается задача минимизации, то неравенства меняют знак на противоположный.

Обозначим через вектор из частных производных L по переменным х,а через – вектор из частных производных L по переменным 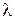. Будем считать, что – вектор-столбец, a – вектор-строка. Для задачи на максимум условия оптимальности примут вид.

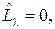
где штрих у матрицы означает транспонирование.

 

Пример: запишем рассмотренную ранее задачу в следующем виде: найти , если .

Мы уже знаем, что функция L не имеет критической точки при x₁, x₂ > 0. Приравняем сначала x₁, а затем x₂ к нулю. При выполнении бюджетных ограничений получаем точки (0,1) и (1/4,0). В точке (0,1) имеем

В точке (1/4, 0) имеем

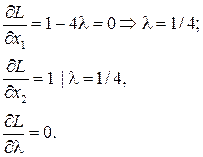
Точка (0,1) удовлетворяет условиям оптимальности, а точка (1/4, 0) – нет.

 

К сожалению, не существует универсального правила для определения, какие из переменных и в каком случае следует приравнять к нулю для получения оптимального решения. В принципе, можно попытаться сначала приравнять к нулю по одной переменной, затем по две, по три и т. д. После этого сравнить значения для всех вариантов и выбрать тот из них, который удовлетворяет условиям оптимальности. Вообще говоря, не более чем переменных могут одновременно обращаться в нуль, так как функциональные ограничения уже определяют т переменных через оставшиеся. Таким образом, вообще говоря, по крайней мере m из условий обращаются в равенства, и этого достаточно для однозначного определения значений т множителей Лагранжа.

В задаче с большим числом переменных и ограничений число групп, в которых k переменных приравнены к нулю, когда k меняется от 1 до ,огромно. Поэтому приведенные условия оптимальности не дают конструктивного метода решения сложных задач.

В экономическом анализе, однако, интересно знать, что случится с условиями оптимальности, когда решение выйдет на границу, определенную ограничением на неотрицательность. Приведенные выше рассуждения дают ответ на этот вопрос. Задачи подобного типа (в которых оптимальное решение достигается на границе области определения целевой функции) часто встречаются в экономической теории при изучении ситуаций, отвечающих изменению параметров условий задачи, перемещающих внутренние точки к границе. Следовательно, для нас представляют интерес нулевые значения компонент решения. Экономическая интерпретация условий оптимальности при нулевых значениях переменных не представляет трудностей. Однако содержательная интерпретация в каждом частном случае зависит от самой задачи.

В случае, когда функция полезности зависит от п переменных, и бюджетное ограничение линейно, условия оптимальности могут быть интерпретированы как требование того, чтобы отношение предельной полезности к цене было одним и тем же для всех действительно потребляемых продуктов и не больше (обычно меньше), чем для непотребляемых продуктов. Если же бюджетное ограничение не одно, интерпретация условий оптимальности может быть более сложной.

Теперь мы можем рассмотреть общую задачу условной оптимизации, содержащую ограничения произвольного вида:

,

Общая задача может быть сведена к случаю, рассмотренному в предыдущем пункте, в котором введены ограничения на неотрицательность, а функциональные ограничения оставлены в форме равенств. Это осуществляется путем введения неотрицательных переменных z_i. При этом i -e ограничение-неравенство заменяется парой соотношений

В полученной задаче переменных; х и z – соответственно п- и m -мерные векторы. Ограничения на неотрицательность наложены на все переменные.

Построим функцию Лагранжа

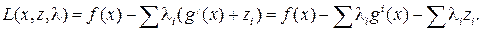
Условия оптимальности по x_j те же, что и прежде. Условия оптимальности по z_i имеют вид

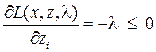и либо , либо .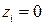

Эти условия не влияют непосредственно на выбор х. Их сущность полностью определяется эквивалентным утверждением

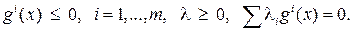
Следовательно, если составить функцию Лагранжа, не учитывающую неравенства в функциональных ограничениях, в виде

и добавить при этом условия неотрицательности , тогда все точки, являющиеся оптимальными относительно z в функции , удовлетворяют условию

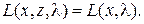
Рассмотрим .По условию , а из условий оптимальности по z применительно к имеем и либо

gⁱ (x) = 0, либо . Отсюда следует, что

, либо оба одновременно.

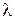Приведенные выше условия можно рассматривать как условия минимума относительно при заданном ограничении на неотрицательность .

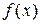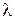Решаем задачу на условный максимум ,и хотя мы в состоянии исследовать на максимумпо ,теперь мы находим минимумпо 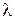выражения, аналогичного классической функции Лагранжа.

Что послужило основанием для таких рассуждений?

Прежде всего, заметим, что в строго классическом случае имеем для всех i. Поэтому, если заменить оптимальную точку 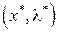на , где 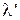– произвольный m -мерный вектор, то

.

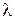Это означает, что на максимальное значение не влияют изменения на допустимом множестве. В строго классической задаче можно было бы исследовать на минимум по 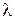с таким же успехом, как и на максимум. Ничего бы при этом не изменилось. Нам, однако, удобнее рассматривать задачу на максимум.

Далее заметим, что в исследуемом случае в любой оптимальной точке , независимо от того, рассматривается ли максимум или минимум по 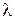, имеет место либо , либо 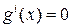. Следовательно, и в задаче на максимум, и в задаче на минимум по 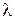в любой оптимальной точке .Это соотношение определяется функциями ограничений, а не целевой функцией.

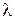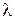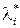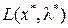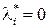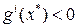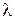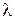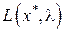Рассмотрим влияние малых вариаций относительно оптимального значения ,учитывая при этом неотрицательность значений . Пусть положительно, тогда . Следовательно, не меняется, как и в классическом случае. Если же , может случиться так, что . Из-за неотрицательности единственная возможная вариация относительно есть некоторая положительная величина . В этом случае член – в выражении для имеет положительный знак, и . Таким образом, в оптимальной точке достигает минимума по 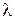.Свойство минимума выявляется только тогда, когда, по крайней мере, одно ограничение неэффективно.

Подытожим свойства оптимальной точки 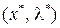для общей задачи оптимизации:

,

.

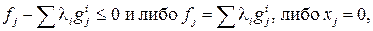
В экономическом анализе мы часто не пытаемся выяснить, является ли некоторая точка оптимальной, а только интересуемся свойствами точки, про которую известно, что она оптимальна. В таких случаях вторые условия устанавливают, что можно игнорировать ограничения, неэффективные в оптимальной точке.

Если рассматривается задача минимизации, то знак неравенств в первом условии нужно поменять на противоположный.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: