 |
Постановка задачи оптимального управления
|
|
|
|
Оптимизация – нахождение всех максимизирующих или минимизирующих элементов или седловых точек – лежит в основе экономического анализа. В пассивных экономических моделях (таких как изучающие общее равновесие) нас интересует оптимальное поведение лица, принимающего решение. В активных моделях (таких как модели эффективного роста) мы сами заинтересованы в получении оптимума. В последние годы появилась тенденция к переходу от моделей типа ««затраты-выпуск»«к моделям анализа производственных процессов, от простейших моделей роста к моделям, изучающим траектории оптимального и эффективного роста. В макроэкономических политико-ориентированных моделях, где оптимизация, в основном, порождена параметрическими оценками, направление исследований изменилось в сторону более сложных моделей выбора оптимальной политики.
Действительно, при соблюдении некоторых ограничений оптимизация рассматривалась многими авторами как определяющая сущность экономики. Значительное развитие теории оптимизации за последние двадцать лет привело к целому ряду различных методов анализа. Поэтому желательно дать общее описание постановки задачи оптимизации и показать, в какой мере различные методы соответствуют этой постановке.
В рассматриваемой задаче все переменные будут задаваться как составляющие векторов из Rn
Будем рассматривать n -мерный вектор 
как функцию его индексов 
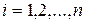. Если заменить индексы непрерывным параметром 
, 
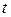может рассматриваться как бесконечно-мерный аналог вектора из Rn. Величина является неизвестной функцией 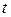, а не точкой, которая может быть задана перечислением ее координат. Задачи оптимизации, в которых неизвестными являются функции, а не точки, в лучшем случае сводятся к области задач вариационного исчисления.
|
|
|
Кроме вектора будем рассматривать:
· допустимое множество К [6]. В задаче будут учитываться только те векторы ,которые принадлежат 
;
· однозначную непрерывную целевую функцию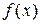 
,значения которой будут оптимизироваться при условии, что 
.
Таким образом, формально задачу максимизации можно записать следующим образом: найти 
такой, что 
для всех .
Если такой х* существует, то задача имеет слабый глобальный максимум (слабый, так как удовлетворяет нестрогому (слабому) неравенству, глобальный, так как неравенство справедливо для всех ).Не следует путать глобальный оптимум с оптимумом в задаче без ограничений. Последнее означает, что К = Rn. Будем считать максимум сильным,если можно найти такой х*,что 
для всех 
.
Существование слабого оптимума допускает неединственность оптимальной точки, так как любой ,удовлетворяющий уравнению 
,также является оптимальной точкой. Сильный оптимум всегда единственен.
Если поменять знак неравенств, получим слабый или сильный минимум. Минимум 
дает максимум для 
.Значение х* часто называют просто решением задачи на оптимум. Во многих экономических моделях решениями называют и другие понятия. Чтобы не путать их, обычно решение нашей задачи называют оптимальным решением.
Большинство известных методов не пригодно для решения поставленной выше задачи. Обычно можно решить задачу следующего вида: найти такой, что для всех 
, где Е – окрестность х* [7].Такая точка называется слабым локальным максимумом. Аналогично можно определить сильный локальный максимум, а также слабый или сильный локальный минимум. Некоторые авторы используют термины относительныйи абсолютный,а не локальный и глобальный оптимум.
Очевидно, если функция имеет оптимум, она должна иметь глобальный оптимум, который должен быть также локальным. С другой стороны, локальный оптимум не обязательно будет глобальным. Прежде всего, нас интересует глобальный оптимум. Интересно выяснить условия, которые надо наложить на постановку задачи для того, чтобы локальный оптимум был также и глобальным. Такие условия (применимые во многих экономических ситуациях) будут приведены ниже. Если они не выполняются, придется применить специальные процедуры (такие как перечисление и сравнение всех локальных оптимумов), чтобы установить глобальный оптимум. Постановка задачи сама определяет, будет ли оптимум сильным или нет. Следует заметить, что сильный локальный оптимум не обязательно единственен, так как может принимать оптимальное значение в нескольких различных точках, каждая из которых будет сильным локальным оптимумом.
|
|
|
Допустимое множество может быть определено несколькими способами. В дискретном случае (в случае дискретных переменных) оно даже может быть описано перечислением. Однако типичное допустимое множество определяется равенствами или неравенствами, описывающими соотношения между переменными. Соотношения, которые определяют допустимое множество, называются ограничениямизадачи. Одно ограничение определяет некоторое множество значений переменных. Если ограничений больше чем одно, возможные значения переменных должны удовлетворять всем ограничениям. Таким образом, допустимое множество является пересечением всех множеств, определяемых каждым из ограничений. На рис. 17.1 а рассматриваются два ограничения:
.
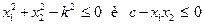Рисунок 17.1 Допустимые множества
Первое ограничение определяет круг радиуса k,второе – область, отделенную от начала координат двумя ветвями равнобокой гиперболы.
В этом случае допустимое множество определяется на рисунке двумя жирно очерченными незаштрихованными областями в I и III квадрантах. Обычно интерес представляет только одна из этих областей из-за естественного в ряде случаев ограничения 
, которое исключает область, расположенную в отрицательном квадранте.
Выделим ограничения типа . Будем называть их прямыми ограничениями на переменные. Ограничения типа представленных выше окружностью и гиперболой будем называть функциональными ограничениями. Более типично, чем на рис. 16.5 а,связь между функциональными и прямыми ограничениями представлена на рис. 16.5 б.Здесь функциональное ограничение очерчивает круг, а прямые ограничения составляют только четверть этого круга.
|
|
|
Оба рассмотренных допустимых множества ограничены, то есть они могут быть заключены в окружность конечного радиуса. Если на рис. 16.5 аопустить первое ограничение и оставить только неравенство, определяемое гиперболой, и прямые ограничения, то допустимое множество будет неограниченным.
Ограничения задают допустимое множество, однако оно может быть пустым. Вернемся к рис. 16.5 а.Если достаточно сократить радиус круга, окажется, что не существует точек, лежащих внутри круга и внутри области, определяемой ветвями гиперболы. Будем называть ограничения несовместными,если допустимое множество пусто.
Для применения некоторых методов и для того, чтобы гарантировать, что локальный оптимум является глобальным, потребуем выпуклости допустимого множества. Допустимые множества на рис. 16.5 (рис. 16.5 а учитывает неотрицательность переменных) выпуклы. Поменяем на рис. 16.5 б в ограничении, описываемом окружностью, знак на противоположный. Тогда допустимое множество представляет собой положительный квадрант без четверти круга с центром в начале координат. Эта область не выпукла.
Границы допустимых множеств важны при рассмотрении задач оптимизации. Рассмотрим их более подробно. Пусть допустимая область определена неравенством 
. Для любой точки из допустимого множества 
выполняется либо
,
либо
В первом случае можно найти такую окрестность точки ,что неравенство будет выполняться для любой точки из этой окрестности. Тогда 
– внутренняяточка допустимого множества (она принадлежит множеству вместе с некоторой окрестностью).
Если же точка удовлетворяет равенству, то в любой окрестности существуют такие точки 
и 
,что 
, а 
. В этом случае – граничная точка, поскольку любая ее окрестность содержит допустимые и недопустимые точки.
Уравнение 
определяет границу рассматриваемого допустимого множества. Поскольку здесь заданы нестрогие ограничения, граница является частью допустимого множества. В этом случае допустимое множество замкнуто. Если же ограничения заданы в виде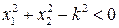 
, граница не принадлежит допустимому множеству. В этом случае допустимое множество открыто. В замкнутом множестве каждая точка либо внутренняя, либо граничная.
|
|
|
В дальнейшем при рассмотрении задач оптимизации будем предполагать, что допустимое множество замкнуто.В противном случае задача часто не имеет решения[8].
Обычно допустимое множество определяется не одним, а несколькими ограничениями. Рассмотрим допустимое множество, определенное несколькими нестрогими неравенствами, и в нем точку 
.Говорят, что данное ограничение эффективно в точке ,если оно в этой точке обращается в равенство. В противном случае ограничение неэффективно в точке .Гиперболическое ограничение 
эффективно в точке 
и неэффективно в точке 
.
Ограничение, определенное как равенство, конечно, всегда эффективно.
|
|
|
