 |
Условия второго порядка для классической задачи на условный оптимум
|
|
|
|
До сих пор мы работали с условиями первого порядка,то есть с условиями, необходимымидля того, чтобы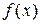 
имела максимум или минимум в точке х *.Эти условия дают критические точки 
. Однако они не показывают, является ли критическая точка максимумом или минимумом функции .
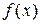В этом пункте будут рассмотрены условия второго порядка.Это так называемые «достаточные»условия того, что х* дает локальный максимум или минимум. Строго говоря, термин «достаточные» здесь не совсем уместен. Условия первого порядка необходимы, а условия первого и второго порядка необходимы и достаточны, но сами по себе условия второго порядка не являются достаточными условиями оптимальности. Тем не менее, этот термин общепринят. При этом неявно предполагается, что условия первого порядка уже выполнены.
При изложении классической задачи на условный оптимум редко приводится полное рассмотрение условий второго порядка. Исключение составляет случай одного ограничения. Ввиду важности условий второго порядка для математической экономики здесь рассматривается общий случай.
Условия второго порядка на безусловный максимум или минимум хорошо известны. Они были получены при разложении функции в ряд Тейлора в точке оптимума и изучении условий, при которых в разложении член второго порядка всегда положителен (в случае минимума) или отрицателен (в случае максимума). Соответствующие утверждения, основанные на свойствах квадратичных форм, обычно выражаются в терминах матриц Гессе – матриц из частных производных второго порядка и их главных миноров.
В этом пункте подобные условия устанавливаются для задачи на условный оптимум. Утверждения, которые будут установлены, во многих отношениях аналогичны соответствующим результатам для задачи на безусловный оптимум.
|
|
|
Функци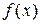и и достигают максимума или минимума при одних и тех же значениях х. Может показаться, что можно исследовать как целевую функцию на безусловный оптимум и использовать при этом обычные методы. Однако это не так. Этого нельзя делать по двум причинам. Во-первых, не имеет максимума или минимума по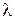 
,таккак для оптимального х *имеем 
и, следовательно, 
не зависит от .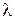
Во-вторых, здесь не все изменения х допустимы, как в случае задачи на безусловный оптимум.
Поэтому мы будем анализировать условия второго порядка для 
,рассматривая только как функцию от х. При этом будем предполагать, что х удовлетворяет заданным ограничениям.
Разложим в точке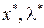 
в ряд Тейлора. Член второго порядка имеет вид
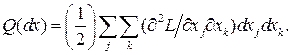
Вариации dx должны удовлетворять ограничениям
Точка 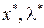дает минимум (максимум), если 
для всех dx,удовлетворяющих ограничениям. Ограничения, заданные в дифференциальной форме, линейны. Следовательно, мы ищем условия, при которых квадратичная форма положительна (или отрицательна) для переменных, удовлетворяющих системе линейных ограничений.
Обозначим через L симметричную матрицу порядка 
,элементы которой равны
а через G – матрицу порядка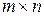 
,составленную из производных по х функций ограничений 
.
Тогда условия второго порядка примут вид (здесь dx заменен на у):
при условии, что 
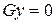(минимум),
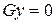при условии, что (максимум).
Чтобы использовать эти результаты, образуем окаймленную матрицу
Матрица 
имеет порядок 
,так как G – матрица порядка 
G’ – порядка 
, а нулевая подматрица соответственно порядка 
.
Сформулируем достаточные для выполнения условий второго порядка условия:
1. задача на минимум:определитель матрицы и все главные миноры порядка, больше чем m + 1 должны иметь знак 
, где m – число ограничений задачи;
2. задача на максимум:определитель матрицы должен иметь знак 
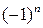, где n – число переменных в задаче. Главный минор порядка 
(главный минор наиболее высокого порядка) должен иметь отрицательный знак. Последующие по величине порядка главные миноры до главного минора порядка 
должны иметь чередующиеся знаки.
|
|
|
Заметим, что эти условия достаточны, но не необходимы для выполнения условий второго порядка. Условия второго порядка могут выполняться, а приведенные условия относительно знаков определителя матрицы и его главных миноров – нет.
Матрица содержит множители Лагранжа, которые могут быть исключены при использовании условий первого порядка. Тогда матрица будет зависеть только от первых и вторых частных производных целевой функции и функций ограничений. Условия второго порядка определяются свойствами функций ограничений и целевой функции.
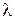Пусть задача содержит только одно ограничение. В этом случае структура матрицы и исключение существенно упрощаются. Для задачи с одним ограничением и двумя переменными имеем
.
Вместо 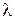можно подставить 
либо 
.
Условия упрощаются, если (что встречается довольно часто в экономическом анализе) функция ограничений либо целевая функция линейны.
Пусть линейна функция ограничений, то есть 
имеет вид 
.Тогда 
,a 
. Заменим 
на 
где 
(из условий первого порядка):
Матрица отличается от 
– окаймленной матрицы Гессе функции f – только первой строкой и первым столбцом. Первая строка (первый столбец) матрицы получается из первой строки (первого столбца) матрицы умножением всех ее (его) элементов на k:
Из свойств определителя следует, что 
. Такое же соотношение справедливо и для соответствующих главных миноров. Следовательно, знаки определителей и главных миноров матриц и одинаковы. Поэтому условия второго порядка выражают в терминах .
Пусть теперь функция ограничений нелинейна, а целевая функция линейна. Тогда 
. Элементы подматрицы 
матрицы имеют вид 
.Элементы окаймления представляют собой первые производные g. Поэтому в этом случае получим
Обозначим теперь через окаймленную матрицу Гессе функции g. Умножая каждую строку матрицы на – 
, получим новую матрицу 
такую, что
где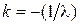 
.
Определители 
и det и их главные миноры связаны такими же соотношениями, что и в предыдущем случае. Но здесь 
.Чтобы получить главный минор порядка п (главный минор наибольшего порядка) матрицы из соответствующего главного минора матрицы , необходимо каждую строку умножить на 
. Такая же связь имеет место и для главных миноров меньших порядков. Следовательно, главные миноры порядка 
будут различаться множителем 
.
|
|
|
Таким образом, в случае линейности целевой функции и 
(что имеет место в типичных экономических моделях) отношение последовательных главных миноров матрицы имеет знак, противоположный знаку отношения соответствующих главных миноров матрицы , и, следовательно, противоположный знаку отношения главных миноров окаймленной матрицы Гессе .
Теперь подытожим правила для важного в экономике случая, когда имеется только одно ограничение и при этом целевая функция либо функция ограничений линейна.
Рассмотрим классическую задачу на условный оптимум, содержащую только одно ограничение.
Пусть целевая функция либо функция ограничений (но не обе одновременно) линейна. Рассмотрим последовательность, состоящую из определителя окаймленной матрицы Гессе нелинейной функции и его главных миноров убывающих порядков вплоть до второго.
Для того чтобы критическая точка представляла собой локальный максимум или минимум, достаточно, чтобы
1. в задаче на максимум члены последовательности имели чередующиеся знаки, если линейна функция ограничений, и одинаковые знаки, если линейна целевая функция;
2. в задаче на минимум члены последовательности имели одинаковые знаки, если линейна функция ограничений, и противоположные, если линейна целевая функция.
Еще раз подчеркнем, что приведенные выше условия достаточные, но не необходимые для локального максимума или минимума[9].
|
|
|
