Существование оптимальных решений

Для установления условий существования оптимальных решений можно использовать вышеприведенные теоремы. Уже было показано, что в общей задаче оптимизации оптимальное решение существует, если функция Лагранжа имеет седловую точку. Теперь установим достаточные условия существования седловой точки.

Рассмотрим функцию Лагранжа, записанную в форме

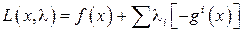
с ограничениями .

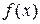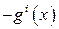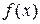Функция линейна по .Это означает, что она может рассматриваться как выпуклая по .Функция Лагранжа как функция от х является положительной линейной комбинацией функций и .Функция ,конечно, будет вогнутой по х,если определяющие ее функции вогнуты. Однако вогнута, если выпукла. Следовательно, вогнута по х,если вогнутая, а все выпуклые функции.

Рассмотрим теперь множества, которым принадлежат х и . Единственное ограничение на – требование неотрицательности. Следовательно, вектор определен на выпуклом множестве (неотрицательный ортант). Если – выпуклая функция, то множество выпукло. Допустимое множество является пересечением выпуклых множеств и поэтому выпукло.

Таким образом, мы показали, что векторы х и определены на выпуклых множествах. Необходимо, чтобы эти множества были компактами. Вид ограничений гарантирует, что множества замкнуты. Остается показать их ограниченность. Поскольку мы ищем минимум , а ограничены снизу требованием неотрицательности , можно выбрать произвольную верхнюю грань, достаточно большую, чтобы не повлиять при этом на оптимальное решение. Труднее обстоит дело с требованиями к допустимому множеству для х. Нельзя избежать добавления специального предположения о том, что допустимое множество ограничено.

Таким образом, если 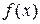вогнутая функция, каждая – выпуклая функция, а допустимое множество ограничено (и не пусто), то функция Лагранжа удовлетворяет условиям теоремы II предыдущего пункта. Следовательно, функция Лагранжа обладает седловой точкой, а общая задача оптимизации имеет решение. Более того, условия глобального оптимума удовлетворяются при тех же условиях выпуклости – вогнутости.

Теорема существования: общая задача максимизации всегда имеет решение, если f (x) – вогнутая, все – выпуклые функции и допустимое множество – ограничено и не пусто.

При выполнении этих условий функция Лагранжа 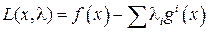обладает седловой точкой 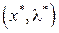, где х^* – оптимальная точка задачи максимизации, а . Кроме того, значения удовлетворяют условиям Куна-Таккера, достаточным для глобального оптимума. Если 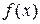строго вогнута, точка х^* – единственна.

Для того чтобы охватить случай, когда 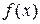и – положительные монотонные преобразования вогнутой и выпуклых функций соответственно, теорема может быть обобщена.

Заметим, что задача линейного программирования удовлетворяет этим условиям выпуклости – вогнутости. Если прямая задача имеет оптимальное решение, ее допустимое множество должно быть не пустым и может рассматриваться как ограниченное. Поскольку в этом случае функция Лагранжа должна иметь седловую точку, а в функции Лагранжа совпадать с оптимальным решением у^* двойственной задачи, можно закончить доказательство теоремы существования решения задачи линейного программирования, утверждая, что если прямая задача имеет решение, то и двойственная также имеет решение.

Обычно условия теоремы существования требуют, чтобы функции были вогнуты, потому что ограничения имеют вид , а в функции Лагранжа они умножаются на и прибавляются к целевой функции 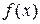.Эти условия эквивалентны приведенным выше.

Условия теоремы являются довольно жесткими, требуя выпуклости каждой функции ограничений и вогнутости целевой функции. Условия второго порядка оперировали вогнуто-выпуклыми функциями. Однако классические условия не гарантируют глобальный оптимум.

Часто можно выбрать в некотором смысле лучший из двух методов. Если число ограничений меньше числа переменных, и ограничения на неотрицательность х неэффективны в оптимуме, можно ожидать, что все функциональные ограничения будут эффективными. Таким образом, можно ввести неравенства в функциональные ограничения и использовать условия глобального оптимума для общего случая, а условия Куна-Таккера сведутся к обычным условиям первого порядка классической задачи. Таким образом, можно показать, например, что решение классической задачи на потребление при условии, что ,дает глобальный оптимум, если .

ГЛАВА 18