 |
Методы решения многокритериальных задач
|
|
|
|
Первый подход к решению многокритериальных задач управления связан с процедурой образования обобщенной функции 
, монотонно зависящей от критериев 
, которая называется процедурой свертывания критериев. Рассмотрим некоторые методы свертывания.
Метод аддитивной оптимизации. Пусть
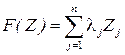. (18.12)
Здесь выражение (18.12) определяет аддитивный критерий оптимальности. Величины 
являются весовыми коэффициентами, которые определяют в количественной форме степень предпочтения j- го критерия по сравнению с другими критериями. Таким образом, коэффициенты определяют важность j- го критерия оптимальности. При этом более важному критерию приписывается больший вес, а общая важность всех критериев равна единице, т.е.
. (18.13)
Обобщенная функция цели (18.12) может быть использована для свертывания векторного критерия оптимальности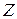 
, если о его компонентах 
известна следующая информация:
частные (локальные) критерии количественно соизмеримы по важности, т.е. каждому из них можно поставить в соответствие некоторое число , которое численно характеризует его важность по отношению к другим критериям;
частные критерии являются однородными (имеют одинаковую размерность – доходы, расходы).
В этом случае для решения задачи векторной оптимизации (18.1) – (18.3) оказывается справедливым применение аддитивного критерия оптимальности (18.12). Подтверждением этого может служить лемма Карлина (1959 год), которая гласит, что, если для некоторых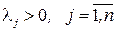 
, (18.14)
где вектор 
оптимален по Парето.
Действительно, если не оптимальное решение по Парето, то тогда существует такой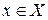 
, что
, (18.15)
причем хотя бы одно неравенство строгое. Умножая каждое неравенство на 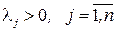и складывая, получаем
|
|
|
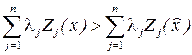, (18.16)
что противоречит (18.14) и доказывает справедливость утверждения леммы.
Эта лемма показывает, что выбор определенной точки среди множества оптимальных по Парето точек эквивалентен указанию весов по каждого критерия. На этом утверждении основано большинство методов.
Требование нормализации критериев возникает в тех задачах, в которых локальные критерии имеют различные единицы измерения. К настоящему времени разработано большое количество схем нормализации. Рассмотрим некоторые из них.
Определим максимум и минимум каждого критерия , т.е.
;
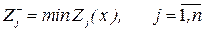
Выделим группу критериев 
, которые максимизируются при решении задачи, и группу критериев 
, которые минимизируются при решении задачи.
Тогда в соответствии с принципом максимальной эффективности нормализованные критерии определяются из соотношений:
,
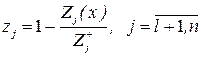или
и обобщенная функция цели имеет вид 
.
В соответствии с принципом минимальной потери нормализованные критерии определяются из соотношений:
(18.17)
или
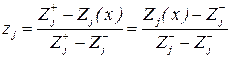(18.18)
и обобщенная функция цели имеет вид 
. Однако в общем виде нормализованные критерии 
могут быть произвольными кривыми, изменяющимися от 0 до 1.
Рассмотрим метод определения весовых коэффициентов относительной важности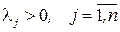 
частных критериев оптимальности по матрице экспертных оценок. Предположим, что проведена групповая экспертиза, в которой каждый из т экспертов назначает свои значения весовых коэффициентов, удовлетворяющие условиям 
, 
. В результате будет получена матрица экспертных оценок
,
где 
- экспертная оценка относительной важности j - го частного критерия оптимальности, предложенная s - м экспертом.
Для назначения оптимально-компромиссных весовых коэффициентов 
, выражающих «коллективное мнение», необходимо задать схему компромисса 
и решить экстремальную задачу:
|
|
|
(18.19)
где 
.
Здесь схема компромисса 
является некоторой мерой близости между вектором 
и элементами матрицы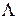 
.
Если мерой близости служит функция
(18.20)
то оптимальным решением задачи (18.19) является вектор средних значений по элементам столбцов матрицы :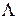
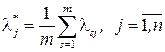(18.21)
Действительно, построим функцию Лагранжа:
Значения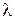 
и 
должны удовлетворять системе уравнений:
(18.22)
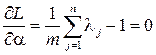(18.23)
Из выражения (18.22) находим
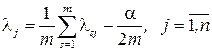(18.24)
Подставляя полученные значения из (18.24) в выражение (18.23), получаем 
, откуда согласно выражению (18.24) следует справедливость формулы (18.21).
На практике эксперты отличаются друг от друга квалификацией, опытом и т.п. Для учета этих факторов вводятся коэффициенты компетентности экспертов 
. Тогда для случая неравнозначности мнений экспертов формула (18.21) может быть обобщена:
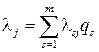(18.25)
Алгоритм решения многокритериальной задачи основан на использовании диалога лица, принимающего решение (ЛПР), с вычислительной машиной. Диалоговая процедура принятия решения представляет собой итеративный процесс обмена информацией между человеком и ЭВМ. Одна итерация состоит из двух следующих шагов:
а) на основе информации, полученной от ЛПР о коэффициентах 
, формулируется задача оптимизации
, (18.26)
которая решается на ЭВМ. Из решения задачи (18.26) находится оптимальная по Парето точка , соответствующая данным весам , и скорость изменения функции 
в точке по различным направлениям, т.е. градиент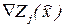 
;
б) на основании полученной информации ЛПР оценивает решение , т.е. определяет, следует ли использовать это решение в качестве окончательного или, если решение неудовлетворительно, на основе значений градиентов 
и опыта работы с объектом корректирует веса , после этого задача (18.26) решается заново:
Динамические многокритериальные задачи определяются конечным или бесконечным набором управлений 
. Например, представляет собой последовательность частных управлений 
, выбираемых в последовательные моменты времени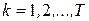 
. Тогда общую многокритериальную задачу управления удается свести к последовательности более простых задач, связанных с частным управлением. В общем виде обобщенная функция цели динамической многокритериальной задачи представляется следующим образом:
|
|
|
Поскольку динамическая задача сводится к решению на каждом шаге статических задач, то на нее переносятся все понятия и утверждения, сформулированные ранее.
Метод многоцелевой оптимизации. Основная идея многоцелевого подхода, выдвинутая еще в начале шестидесятых годов, состоит в назначении в пространстве критериев некоторой цели 
. Это позволяет свести многокритериальную задачу к задаче оптимизации (18.27):
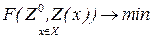(18.27)
где 
есть некоторое расстояние между точками 
и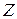
В частности,
(18.28)
или
Задача (18.27) представляет собой задачу целевого программирования и решается методами линейного программирования.
Особого внимания при использовании аппарата целевого программирования в многокритериальных задачах заслуживает выбор вектора весов 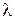, компоненты которого связаны с оценкой «важности» отклонений 
от . В предположении существования и дифференцируемости обобщенной функции цели весовые коэффициенты могут определяться из соотношения
где - произвольно выбранный опорный критерий.
При сделанных предположениях для каждого j -го критерия может быть подобрано такое приращение 
, которое будет полностью компенсировано уменьшением на единицу значения другого критерия. Иными словами, может быть подобрано такое , что для ЛПР будут безразличны (равноценны) комбинации значений критериев и 
, где 
- значение критерия, выбранного в качестве опорного. Тогда
. (18.29)
В общем случае веса будут зависеть от значений . Выдвинутые идеи могут быть реализованы в виде следующего человеко-машинного алгоритма целевой оптимизации.
Этап 1. Для каждой функции определяется предельное значение (цель) 
. Если ЛПР затрудняется или не в состоянии определить значения для всех или некоторых критериев, то в качестве выбирается произвольное число, удовлетворяющее условиям 
.
Этап 2. Определяются подходящая начальная точка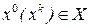 
и вычисляется 
.
|
|
|
Этап 3. Определяется 
путем опроса ЛПР и использования формулы (18.29).
Этап 4. Решается задача математического программирования следующего вида:
(18.30)
(18.31)
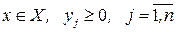(18.32)
Здесь yj определяет расхождение между критерием и целью . В результате решения задачи (18.30) – (18.32) определяется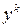 
, 
и наилучшее направление решения многоцелевой задачи 
.
Этап 5. Путем опроса ЛПР определяется величина шага 
, которая минимизирует обобщенную функцию цели 
.
Этап 6. Если 
, то решение заканчивается, в противном случае определяется новое промежуточное решение 
и далее цикл решения повторяется с этапа 3.
Второй подход многокритериальной оптимизации связан с определением частного упорядочения (предпочтения) критериев на множестве решений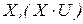 
. Рассмотрим некоторые методы этого подхода.
Метод выделения главного критерия. Допустим, что среди критериев 
удается выделить один – главный, скажем , и установить разумные ограничения по другим целям, которым должно удовлетворять оптимальное решение. Обозначим эти минимальные значения по критериям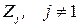 
через . Такая информация позволяет векторную задачу оптимизации свести к скалярной задаче:
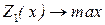(18.33)
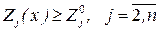(18.34)
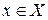(18.35)
Одновременно с решением задачи (18.33) – (18.35) находится вектор оптимальных оценок 
, которые характеризуют влияние на оптимальное значение первой целевой функции изменений уровней других целевых функций, т.е. 
. Оценки 
содержат важную информацию о взаимовлиянии целевых функций. Из уравнения полного дифференциала 
получаем соотношение эквивалентных изменений уровней любых целевых функций. Например, 
и 
, сохраняющие оптимальное значение первой целевой функции, находятся в соотношении 
. Эти соотношения могут использоваться для корректировки первоначально заданных уровней целевых функций.
В качестве максимизируемой в принципе может быть выбрана любая из целевых функций и любая из них может быть ограничиваемой функцией. Таким образом, можно сформулировать и решить п задач оптимизации. В результате анализа оптимальных решений, включающего корректировку уровней целевых функций, область поиска вариантов решений еще более сужается и тем самым облегчается неформальный выбор окончательного решения.
Выбор компромиссного решения на основе решения п задач оптимизации может быть формализован. Пусть 
- вектор оптимальных значений целевых функций, 
- вектор отклонений от ; 
- максимально допустимые отклонения от 
. Можно сформулировать такие задачи скалярной оптимизации:
а) максимизация одной целевой функции при максимально допустимых отклонениях от оптимальных значений других целевых функций:
|
|
|
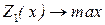(18.36)
(18.37)
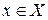(18.38)
б) максимизация разности одной целевой функции и штрафной функции отклонений от оптимальных значений других целевых функций:
(18.39)
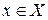(18.40)
где 
- монотонно возрастающая функция.
Легко видеть, что полная формализация выбора компромиссного решения требует принятия дополнительных допущений о значениях 
и вида функции . Этот путь не всегда себя оправдывает.
Метод последовательных уступок. Пусть для определенности все критерии упорядочены по предпочтительности, т.е. 
. Сначала решается задача
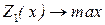(18.41)
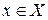(18.42)
Анализируется оптимальное решение 
и 
и далее устанавливается некоторая уступка 
по критерию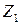 
, на которую ЛПР согласно для того, чтобы улучшить решение по другим критериям. Это приводит к следующей задаче:
(18.43)
(18.44)
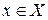(18.45)
Обозначим оптимальное значение полученной целевой функции через 
и продолжим процедуру последовательных уступок описанным образом. На последнем шаге будет решаться задача
(18.46)
(18.47)
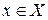(18.48)
и решение этой задачи принимается в качестве решения исходной задачи. Этот метод отличается большой наглядностью. В отличие от метода выделения главного критерия рассматриваемые на каждом шаге задачи имеют решение, а вся процедура сразу приводит к какому-то результату.
|
|
|
