 |
Постановка задачи многоуровневой оптимизации
|
|
|
|
Разработка теории многоуровневой оптимизации – одна из наиболее актуальных задач организационного управления. Ее развитие встречает целый ряд трудностей принципиального характера. Оказывается, например, что анализ (а тем более синтез многоуровневой системы управления) непосредственно не сводится к обычной оптимизации, так как каждое звено такой системы имеет возможность самостоятельно принимать решение.
Введение многоуровневой структуры связано с распределением между ее звеньями различных функций обработки информации и принятия решений. При этом децентрализация процесса управления служит источником неопределенности, которая проявляется в нетождественности интересов всей системы и ее отдельных звеньев. В связи с этим в теории многоуровневого управления возникают проблемы оптимальной централизации и децентрализации функций управления, оптимальной структуризации системы управления, многоуровневой оптимизации принятия решений и т.д.
В самом общем виде структура многоуровневой системы управления может быть представлена следующей схемой (рис. 18.2).
Верхний уровень управления представлен блоком 
, нижний – локальными блоками 
. Производственный процесс определяется блоком 
. Соответственно модель управления верхнего уровня называется либо моделью центра, либо координирующей моделью, а модели управления нижнего уровня называются локальными моделями.
Рис. 18.2. Структура многоуровневой системы управления
Связи, по которым движутся управляющие сигналы «сверху вниз» и отчетные данные «снизу вверх», обычно называют вертикальными. Одновременно локальные блоки одного уровня могут быть связаны между собой информационными связями, имеющими большое значение для управления локальными объектами. Связи такого рода называются горизонтальными.
|
|
|
Таким образом, многоуровневая система управления рассматривается как сложная система с иерархической структурой, внутри которой существуют горизонтальные и вертикальные связи.
В многоуровневой структуре, являющейся формализацией совокупности взаимосвязанных экономических ячеек, на первый план выдвигаются вопросы координации и согласования принятия решений на различных уровнях. Среди задач согласования решений в многоуровневой системе выделяются задачи согласования межуровневого типа и задачи согласования внутриуровневого типа.
В задача межуровневого согласования модель центра обычно интерпретируется как координирующая модель. В этом случае проблема существования согласованных решений преобразуется в известную в теории многоуровневых систем проблему координируемости. Это означает, что здесь должны быть выяснены условия, при выполнении которых решающая система верхнего уровня оказывается в состоянии осуществить согласование решений, используя параметры управления в границах своей компетентности.
В условиях межуровневого согласования общая модель многоуровневой системы обычно представляется следующим образом:
(18.49)
(18.50)
. (18.51)
Здесь 
описывает состояние системы в целом, а вектор 
состояние его j -й подсистемы, 
- целевая функция системы, 
-функция затрат ресурсов системы, 
- локальное множество допустимых решений j -й подсистемы. Модели типа (18.49) – (18.51) называют моделями блочного типа. В соответствии с принципами координации система механизмов межуровневого согласования определяется набором 
, где 
- целевая функция центра; 
- локальные целевые функции подсистем 
; 
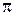- механизмы согласования плановых решений.
Механизмы межуровневого согласования должны обеспечить выбор подсистемы плановых решений, которые удовлетворяют как требованиям системы критериев, так и локальным и глобальным (системным) ограничениям. В основе описания механизмов межуровневого согласования лежат декомпозиционные методы.
|
|
|
При внутриуровневом согласовании не делается заранее предположение о какой-либо глобальной модели системы в целом (в отличие от межуровневого согласования). Предполагается лишь, что для системы сформулирована цель ее функционирования и имеются совершенно самостоятельные задачи для подсистем нижнего уровня. В соответствии с принципами горизонтального взаимодействия система механизмов внутриуровневого согласования определяется набором 
, где - целевые функции подсистем ; 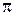– механизмы согласования плановых решений.
Механизмы внутириуровневого согласования должны обеспечить выбор подсистемами плановых решений, которые удовлетворяют как требованиям системы локальных критериев, так и системе локальных и глобальных (балансовых) ограничений. Основными целями анализа взаимодействия при горизонтальных связях являются определение понятия «решение» и проблема построения супермодели, совокупность решений которой совпадает с множеством решений взаимодействующих подсистем. Обычно такая супермодель представляет собой композицию отдельных моделей объектов. В основе описания механизмов внутриуровневого согласования лежат композиционные методы.
Из совокупности моделей подсистем можно составить задачу векторной оптимизации. Решение этой задачи позволяет, как известно, находить равновесные решения (оптимальные по Парето). Но по сравнению с общей задачей векторной оптимизации понятие «равновесное решение» приобретает здесь социально-экономическое содержание. Дополнение модели векторной оптимизации определенным экономическим механизмом позволяет перейти к задаче выбора на множестве равновесных планов. Устройство экономического механизма зависит от конкретных особенностей моделируемых процессов экономического взаимодействия.
Общей чертой всякого экономического взаимодействия является использование цен как измерителей затрат и результатов деятельности каждой подсистемы и взаимоотношений подсистем. При заданных ценах (вектор 
) композиция супермодели может быть представлена:
|
|
|
(18.52)
(18.53)
(18.54)
Эта формализация соответствует тому условию, что подсистемы стремятся к достижению экстремума своих локальных целевых функций (18.52) при соблюдении локальных (18.53) и глобальных (18.54) ограничений системы. Важным здесь является то, что глобальные ограничения не заданы в явном виде, а определяются в процессе согласования плановых решений.
Поэтому при произвольном векторе получаемые локальные решения 
могут не удовлетворять общим для всех подсистем условиям, т.е.
.
Система цен 
называется равновесной, если среди оптимальных планов подсистем, рассчитанных при этих ценах, найдутся такие, которые образуют допустимый план системы в целом, т.е. план, удовлетворяющий общим условиям для всех подсистем.
Пусть 
- множество оптимальных планов j -й подсистемы при векторе . Тогда, в соответствии с определением равновесных цен множества 
содержат планы 
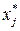, из которых можно составить такую композицию 
, для которой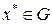 
.
План 
, как правило, принадлежит множеству эффективных планов (множеству по Парето). Такой план характеризует некоторое равновесие экономических интересов подсистем.
Пара 
называется состоянием (траекторией) равновесия, есл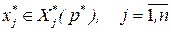и 
и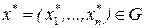 
.
Полученное состояние (траекторию) равновесия не следует понимать как абсолютно наилучшее решение проблемы согласования интересов всех подсистем. Равновесие достигается в рамках установленных принципов и условий экономических отношений. При изменении этих принципов и условий могут получаться иные состояния (траектории) равновесия.
|
|
|
