 |
Решение задач многоуровневой оптимизации
|
|
|
|
Среди методов решения оптимизационных задач большой размерности наибольшее распространение в настоящее время получили алгоритмы блочного программирования [14]. Суть этих методов заключается в разложении исходной задачи на систему взаимосвязанных подзадач, решения которых, скоординированные по определенным правилам, позволяют получить решение первоначальной задачи. Разложение (декомпозиция) исходной задачи и последующая координация частных подзадач могут проводиться различными способами, что и определяет многообразие известных в литературе алгоритмов блочной оптимизации.
Так, например, информативная связь между отдельными подзадачами может осуществляться либо непосредственно, либо через специализированный орган (центр), либо двумя этими способами одновременно, в зависимости от чего (по типу разложения) различают алгоритмы с вертикальными, горизонтальными и смешанными связями. Координация подзадач также может осуществляться по-разному: как с использованием в качестве регулирующих параметров показателей, входящих в целевые функции, так и ограничений подзадач. В зависимости от этого (по характеру координации) выделяют алгоритмы с ценностными (стимулирующими), лимитными и лимитно-ценностными формами регулирования.
Несмотря на имеющиеся алгоритмические особенности, использование методов блочного программирования для решения задач планирования развития экономки основано на общем концептуальном предположении относительно структуры матрицы затрат-выпуска в экономической системе. Оно заключается в том, что не все ресурсы потребляются во всех технологических способах. Точнее говоря, имеются группы ресурсов, каждая из которых используется только для соответствующей группы способов, и имеются группы ресурсов, которые применяются во всех способах. При таком представлении производственных процессов матрицу затрат-выпуска можно привести к блочно-диагональному виду и использовать эти ее свойства для организации эффективного итеративного процесса поиска условного экстремума глобальной целевой функции задачи с блочной структурой ограничивающих условий. Соответственно, с точностью до принятых предпосылок алгоритмы блочного программирования могут интерпретироваться как процедуры составления плана в иерархически организованной хозяйственной системе. Рассмотрим содержание некоторых из них на следующем упрощенном примере линейной статической задачи планирования.
|
|
|
Пусть исходная задача, решаемая неким плановым органом, заключается в распределении лимитированных ресурсов между входящими в его подчинение хозяйственными ячейками. Все ресурсы системы разделены на две группы: общие (глобальные), которые используются различными ячейками, и собственные (локальные), используемые лишь отдельными ячейками. Плановый орган ищет такой вариант распределения глобальных ресурсов, который обеспечил бы максимальный (совокупный) доход по всей системе. При этом каждая ячейка заинтересована в получении максимального дохода от результатов своей деятельности.
Для формализованного описания задачи введем следующие обозначения:
 – индекс технологического способа;
– индекс технологического способа;
 – индекс хозяйственной ячейки;
– индекс хозяйственной ячейки;
 – множество технологических способов, используемых
– множество технологических способов, используемых  -й ячейкой[15];
-й ячейкой[15];
 – индекс ограниченного ресурса;
– индекс ограниченного ресурса;
 – множество видов глобальных ограниченных ресурсов;
– множество видов глобальных ограниченных ресурсов;
 – множество видов локальных ограниченных ресурсов ячейки
– множество видов локальных ограниченных ресурсов ячейки  ;
;
 – доход от единицы продукции, выпускаемой
– доход от единицы продукции, выпускаемой  -м технологическим способом;
-м технологическим способом;
 – норматив затрат
– норматив затрат  -го ресурса на единицу выпускаемой продукции при использовании
-го ресурса на единицу выпускаемой продукции при использовании  -гo технологического способа;
-гo технологического способа;
|
|
|
 – объем ресурсов
– объем ресурсов  -го вида в системе;
-го вида в системе;
 – искомый объем выпуска продукции (интенсивность использования)
– искомый объем выпуска продукции (интенсивность использования)
 -м технологическим способом.
-м технологическим способом.
В принятых обозначениях модель исходной задачи имеет вид
 (18.55)
(18.55)
 (18.56)
(18.56)
 (18.57)
(18.57)
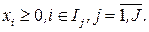 (18.58)
(18.58)
Матрица ограничивающих условий задачи может быть представлена следующим образом:

где  – матрица размерности
– матрица размерности  ,
,
 – матрица размерности
– матрица размерности  .
.
Таким образом, все ненулевые элементы в матрице коэффициентов исходной задачи содержатся либо в подматрицах (блоках), не имеющих между собой общих строк столбцов, либо в некоторой подматрице, не вошедшей ни в один из блоков.
Первой работой в области решения задач типа (18.55) – (18.58) (задач линейного программирования с блочной структурой) явился предложенный Дж. Данцигом и Ф. Вулфом декомпозиционный алгоритм, относящийся в рамках приведенной выше классификации к алгоритмам с вертикальной координацией, использующим ценностную форму регулирования. Основная идея алгоритма Данцига-Вулфа заключается в замене непосредственного решения исходной задачи итеративной процедурой решения серии подзадач: локальных задач (по числу хозяйственных ячеек) и координирующей задачи.
Процедура расчетов строится следующим образом. Координационный центр сообщает ячейкам исходные цены (оценки) на общие ресурсы, после чего в пределах собственных возможностей (локальных ресурсных ограничений) и возможностей получения по указанным ценам общих ресурсов каждая ячейка максимизирует доход от результатов своей деятельности.
Модель локальной задачи, решаемой  -й ячейкой на итерации
-й ячейкой на итерации 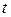 , имеет вид
, имеет вид
 (18.59)
(18.59)
 (18.60)
(18.60)
 (18.61)
(18.61)
После решения локальных задач (18.59) – (18.61) (обозначим их оптимальные планы через  ) каждая ячейка передает в центр информацию о величине дохода
) каждая ячейка передает в центр информацию о величине дохода  и плане выпуска или потребления общих ресурсов
и плане выпуска или потребления общих ресурсов

На основе полученной информации центр решает специальную координирующую задачу, состоящую из ограничений на использование общих ресурсов и линейной целевой функции, коэффициенты которой характеризуют доход от единичной интенсивности потребления ресурсов хозяйственными ячейками. Переменными задачи выступает  – интенсивность использования вариантов планов выпуска и потребления общих ресурсов, представленных ячейками центру.
– интенсивность использования вариантов планов выпуска и потребления общих ресурсов, представленных ячейками центру.
|
|
|
Модель координирующей задачи имеет вид
 (18.62)
(18.62)
 (18.63)
(18.63)
 (18.64)
(18.64)
где  – множество индексов
– множество индексов  при переменных
при переменных  , вошедших в базис на предыдущей итерации.
, вошедших в базис на предыдущей итерации.
После решения координирующей задачи центр передает ячейкам полученные оценки  общих ресурсов для очередного уточнения коэффициентов целевых функций локальных задач по формуле
общих ресурсов для очередного уточнения коэффициентов целевых функций локальных задач по формуле
 .
.
Таким образом, на каждой итерации решение серии локальных задач позволяет установить оптимальную при данных ценах программу деятельности хозяйственных ячеек (потребность в общих ресурсах и объемы выпуска продукции), а решение координирующей задачи – целесообразные изменения стоимостных регулирующих параметров в системе (цен), стимулирующие рост эффективности ее функционирования.
Процесс продолжается до тех пор, пока доход каждой ячейки не станет нулевым, что является необходимым условием оптимальности плана. Однако может оказаться, что совокупность полученных ячейками планов не является допустимой вследствие превышения ограничений по общим ресурсам (если в некоторых локальных задачах имеется бесконечное число планов, максимизирующих значение целевой функции). Поэтому на последнем шаге работы алгоритма с помощью решения координирующей задачи проводится согласование локальных оптимальных планов с целью выполнения всех ресурсных ограничений по системе в целом.
С математической точки зрения рассматриваемый алгоритм является результатом применения техники прямого симплекс-метода к решению некоторой вспомогательной задачи, образуемой из исходной. Каждую итерацию этого алгоритма можно разбить на этапы. К началу первого этапа имеется совокупность столбцов, образующих текущий базис данной итерации, и один или несколько дополнительных столбцов, подлежащих введению в базис. Из этого множества формируется новый базис, по которому рассчитываются новые оценки ресурсных ограничений. На втором этапе, исходя из оценок ограничений, находятся столбцы с положительными (желательно максимальными) оценками соответствующих им переменных. Если таковых не оказывается, то решение получено. В противном случае найденные столбцы подлежат введению в базис на первом этапе следующей итерации.
|
|
|
В литературе известно много различных модификаций декомпозиционной схемы Данцига–Вулфа, связанных либо с использованием других технических приемов решения задачи линейного программирования (двойственного симплекс-метода, метода сокращения невязок Форда–Фулкерсона и т. д.), либо с обобщением принципа декомпозиции для решения линейных задач с более сложной блочной структурой матрицы ограничений, а также для решения задач нелинейного выпуклого программирования. Для всех декомпозиционных методов данного класса доказана глобальная сходимость к оптимальному решению, хотя вычислительные эксперименты свидетельствуют о невысокой скорости этого процесса вблизи точки оптимума.
Ценностное регулирование деятельности хозяйственных ячеек в алгоритмах блочного программирования с вертикальной координацией может осуществляться не только при использовании в качестве управляющих параметров цен (оценок) на продукты и ресурсы, но и путем введения «штрафного» стимулирования. Штрафы могут налагаться либо непосредственно за отклонение выбираемых ячейками планов от желаемых с точки зрения центра плановых вариантов, либо по результатам их деятельности (например, за нарушение ресурсных ограничений, условий выпуска и т. д.).
Пусть, как и в условиях задачи (18.62) – (18.64), центр осуществляет распределение общих лимитированных ресурсов между хозяйственными ячейками, руководствуясь критерием максимизации дохода. В распоряжении центра имеется приблизительная информация о производственных возможностях ячеек, на основе которой он сообщает им не плановые цены на продукты и ресурсы, а сами проекты плана. Причем из-за недостатка у центра информации о реальных возможностях производства может оказаться, что предложенные им проекты плана для ячеек невыполнимы. В этом случае задача ячеек заключается в разработке собственных вариантов плана, в определенном смысле наиболее близких к проекту центра.
Стимулирование ячеек с целью решения подобной задачи осуществляется путем введения штрафов за отклонение предложенных ими вариантов от плана центра. Рассчитываемые при данных условиях в локальных задачах варианты планов передаются в центр и используются там для уточнения информации о производственных возможностях ячеек.
Рассмотрим один из возможных алгоритмов блочного программирования, формализующих приведенную выше процедуру планирования. На итерации 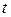 проводится последовательное решение координационной задачи центра и локальных задач хозяйственных ячеек. Модель задачи центра имеет вид
проводится последовательное решение координационной задачи центра и локальных задач хозяйственных ячеек. Модель задачи центра имеет вид
|
|
|
 (18.65)
(18.65)
 (18.66)
(18.66)
 (18.67)
(18.67)
 (18.68)
(18.68)
где

Ограничения (18.67) модели имеют тот же смысл, что и (18.64) задачи центра в методе Данцига–Вулфа, однако накопление в центре информации о производственных возможностях ячеек здесь осуществляется по-иному. Неравенства  для любого
для любого  определяют некоторое полупространство в пространстве переменных
определяют некоторое полупространство в пространстве переменных  . Уточнение информации осуществляется путем задания новых полупространств в ходе следующей процедуры расчетов.
. Уточнение информации осуществляется путем задания новых полупространств в ходе следующей процедуры расчетов.
Пусть  – решение задачи (18.65) – (18.68). На основе этого решения локальная задача для
– решение задачи (18.65) – (18.68). На основе этого решения локальная задача для  -й ячейки формируется следующим образом:
-й ячейки формируется следующим образом:
 (18.69)
(18.69)
 (18.70)
(18.70)
 (18.71)
(18.71)
Величина  характеризует квадратичное отклонение возможных вариантов плана хозяйственной ячейки
характеризует квадратичное отклонение возможных вариантов плана хозяйственной ячейки  от проекта центра
от проекта центра  и представляет собой штраф, накладываемый на ячейку за рассогласование плановых решений.
и представляет собой штраф, накладываемый на ячейку за рассогласование плановых решений.
Пусть 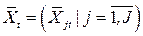 – вариант плана, найденный ячейками по результатам решения серии задач (18.69) – (18.71). Новые полупространства в ограничениях (18.67) формируются по правилам
– вариант плана, найденный ячейками по результатам решения серии задач (18.69) – (18.71). Новые полупространства в ограничениях (18.67) формируются по правилам

Эти величины позволяют центру уточнить информацию о производственных возможностях ячеек и разработать новый вариант плана  [16].
[16].
Другой класс алгоритмов блочного программирования образуют методы с вертикальной координацией, использующие лимитную форму регулирования. Наиболее известным из них является метод «планирования на двух уровнях» Корнай–Липтака, на примере которого применительно к задаче (18.65) – (18.68) мы и познакомимся с данным типом декомпозиционных процедур.
При расчетах по методу Корнай–Липтака центр сообщает хозяйственным ячейкам информацию об объемах общих лимитированных ресурсов, которые предоставляются в их распоряжение. Каждая ячейка решает задачу максимизации дохода при ограничениях на потребление общих ресурсов (в пределах, установленных центром) и локальных ограничениях. Полученные варианты выпуска продукции и потребления общих ресурсов, а также оценки этих ресурсов в оптимальных планах локальных задач поступают в координирующую задачу центра. Сопоставляя оценки по общим ресурсам, центр устанавливает тенденции изменения их распределения между ячейками: там, где оценки низкие, их объемы уменьшаются, а там, где относительно высокие, – увеличиваются.
В алгоритмах с лимитными формами регулирования проблема оптимального распределения ресурсов, решаемая центром, связана с построением зависимостей совокупного дохода системы от конкретных и допустимых вариантов распределения ресурсов между ячейками (т. н. координирующей функции) и последующей ее оптимизацией [17]. В методе Корнай–Липтака координирующая функция на каждой итерации аппроксимируется линейной функцией, построенной на основе оценок. В связи с тем, что целевая функция задачи центра при этом оказывается неограниченной, устанавливается регламент (верхние ограничения) на объемы распределяемых ресурсов, а для обеспечения сходимости алгоритма вводится специальная процедура усреднения решений на последовательных итерациях.
Опишем схему расчетов на 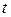 итерации работы алгоритма для задачи (18.65) – (18.68): исходя из предложенного центром варианта распределения общих ресурсов
итерации работы алгоритма для задачи (18.65) – (18.68): исходя из предложенного центром варианта распределения общих ресурсов  , каждая ячейка решает следующую оптимизационную задачу:
, каждая ячейка решает следующую оптимизационную задачу:
 (18.72)
(18.72)
 (18.73)
(18.73)
 (18.74)
(18.74)
 (18.75)
(18.75)
Пусть  – решение серии локальных задач, а
– решение серии локальных задач, а  – оценки общих ограничений,
– оценки общих ограничений,  . Тогда новое приближение к решению
. Тогда новое приближение к решению  находится путем усреднения решений, полученных на предыдущей итерации и
находится путем усреднения решений, полученных на предыдущей итерации и  :
:
 (18.76)
(18.76)
где  удовлетворяет условиям
удовлетворяет условиям

Далее центром решается задача перераспределения по каждому общему ресурсу  :
:
 (18.77)
(18.77)
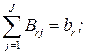 (18.78)
(18.78)
 (18.79)
(18.79)
Верхняя и нижняя границы  и
и  допустимых объемов распределения ресурсов в ограничениях (18.79) могут устанавливаться из различных соображений. Например, можно считать
допустимых объемов распределения ресурсов в ограничениях (18.79) могут устанавливаться из различных соображений. Например, можно считать  , а в качестве
, а в качестве  выбрать постоянное число, заведомо большее, чем оптимальное распределение
выбрать постоянное число, заведомо большее, чем оптимальное распределение  .
.
Результаты решения задачи (18.67) – (18.69) позволяют установить новый вариант распределения общих ресурсов  , который сообщается ячейками, после чего процесс повторяется.
, который сообщается ячейками, после чего процесс повторяется.
В результате итеративных расчетов разница в оценках общих ресурсов между отдельными ячейками может стать сколь угодно малой, то есть процесс сходится (хотя, как правило, немонотонно) к оптимальному решению. Для ускорения сходимости алгоритма в практических расчетах вместо процедуры усреднения (18.66) обычно используют более сложные эвристические процедуры нахождения экстремума координирующей функции.
С позиций отражения реального механизма принятия решений более адекватными практике планирования являются методы блочной оптимизации, использующие смешанную, лимитно-ценностную форму регулирования, при которой центр координирует деятельность хозяйственных ячеек с помощью различных параметров управления (цен на продукцию и ресурсы, штрафов по результатам деятельности, лимитного распределения ресурсов и т. д.). В настоящее время в литературе предложен ряд алгоритмов подобного типа, основанных на комбинации методов штрафных функций и множителей Лагранжа[18].
Рассмотрим на примере одной из предложенных процедур содержательный аспект этого класса алгоритмов. Предварительно в исходной задаче (18.65) – (18.68) условие (18.66) представим в виде
 (18.80)
(18.80)
 (18.81)
(18.81)
Составим для полученной задачи модифицированную функцию Лагранжа вида
 (18.82)
(18.82)
при фиксированных  и
и  , удовлетворяющих условиям (18.67), где нижний индекс
, удовлетворяющих условиям (18.67), где нижний индекс  означает, что отрицательное число заменяется нулем.
означает, что отрицательное число заменяется нулем.
Итеративный процесс расчетов строится следующим образом. Пусть на предыдущей  итерации получены значения оценок ресурсных ограничений
итерации получены значения оценок ресурсных ограничений  и выпуска продукции
и выпуска продукции  . Центр сообщает хозяйственным ячейкам информацию о ценах на ресурсы и об объемах ресурсов, выделяемых в их распоряжение, которые рассчитываются по формуле
. Центр сообщает хозяйственным ячейкам информацию о ценах на ресурсы и об объемах ресурсов, выделяемых в их распоряжение, которые рассчитываются по формуле
 (18.83)
(18.83)
(то есть распределение ресурсов центром определяется по значениям, полученным на предыдущей итерации).
Каждая ячейка решает свою оптимизационную задачу вида
 (18.84)
(18.84)
 [19], (18.85)
[19], (18.85)
тем самым определяя вариант плана с учетам штрафов за возможное превышение ресурсных лимитов, установленных центром.
Информация о предварительном варианте плана  передается в центр, где рассчитываются предварительные оценки ресурсов
передается в центр, где рассчитываются предварительные оценки ресурсов
 , (18.86)
, (18.86)
где  – параметр,
– параметр,  , а затем определяется окончательный (для
, а затем определяется окончательный (для 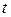 -й итерации) вариант плана и цен:
-й итерации) вариант плана и цен:
 (18.87)
(18.87)
 ,
,
где  – параметр,
– параметр,  [20].
[20].
После этого цикл расчетов повторяется.
|
|
|


