 |
Координация в решении задач многоуровневой оптимизации
|
|
|
|
В действительности в процессе планирования возникает необходимость согласования решений не только между различными уровнями организационной иерархии, но и в горизонтальном разрезе системы (между объектами одного уровня). «Горизонтальная» взаимоувязка решений в настоящее время является одной из наиболее сложных и актуальных проблем теории и практики планирования развития экономических систем. Поэтому особый интерес представляют алгоритмы блочного программирования с горизонтальной координацией деятельности хозяйственных объектов.
В литературе различают несколько типов алгоритмов с горизонтальной координацией (алгоритмы с последовательной возвратно-поступательной и циклической координацией, алгоритмы с параллельной координацией и т. д.), которые различаются структурой взаимосвязей между подзадачами, характером формирования управляющих параметров и т. д. Познакомимся с данным классом декомпозиционных процедур на примере одного из алгоритмов с горизонтальной последовательной координацией.
Предположим, что речь идет о задаче планирования развития комплекса взаимосвязанных производств, определенным образом упорядоченных по глубине обработки исходного сырья. Задачи хозяйственных ячеек (соответствующих этим производствам) обладают следующей особенностью. Множества их ограничивающих условий можно разделить на две части: первая из них – ограничения, правые части которых зависят от решений задач для последующих производств (связывающие ограничения)[21], вторая – локальные ограничения (например, ресурсные), содержащие только параметры данной ячейки. Целевая функция задачи (будем считать ее доходом) также включает две группы слагаемых. В первой из них учитываются непосредственные результаты деятельности данной хозяйственной ячейки, вторая зависит от деятельности предшествующих звеньев, которая определяется через оценки связывающих ограничений.
|
|
|
Введем следующие обозначения:
 – матрица затрат-выпуска для ячейки
– матрица затрат-выпуска для ячейки  ;
;
 – оценки связывающих ограничений задачи ячейки
– оценки связывающих ограничений задачи ячейки  ,
,  ;
;
 – пропорции выпуска конечной продукции ячейкой
– пропорции выпуска конечной продукции ячейкой  ;
;
 – число комплектов этой продукции в ячейке
– число комплектов этой продукции в ячейке  ;
;
 – стоимостные оценки конечной продукции для ячейки
– стоимостные оценки конечной продукции для ячейки  ;
;
 и
и  – параметры локальных ограничений для ячейки
– параметры локальных ограничений для ячейки  ;
;
 – искомый объем выпуска продукции ячейкой
– искомый объем выпуска продукции ячейкой  .
.
В принятых обозначениях модель задачи для  -й ячейки записывается следующим образом:
-й ячейки записывается следующим образом:
 (18.88)
(18.88)
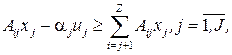 (18.89)
(18.89)
 (18.90)
(18.90)
Взаимодействие ячеек в рамках рассматриваемой процедуры осуществляется следующим образом. Пусть на предыдущей  итерации найдены решения
итерации найдены решения  , которые вводятся в правые части связывающих ограничений (18.89) задач на
, которые вводятся в правые части связывающих ограничений (18.89) задач на 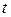 -й итерации. Итерация начинается с решения первой задачи, информация об оценках связывающих ограничений которой поступает во все последующие задачи. Далее решается вторая задача, и ее оценки
-й итерации. Итерация начинается с решения первой задачи, информация об оценках связывающих ограничений которой поступает во все последующие задачи. Далее решается вторая задача, и ее оценки  передаются следующим ячейкам и т. д. до задачи
передаются следующим ячейкам и т. д. до задачи  . Первый этап итерации
. Первый этап итерации 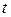 на этом заканчивается, и начинается второй этап, на котором решение задач проводится в обратной последовательности. Регулирующим параметром на этом этапе выступают объемы выпуска продукции
на этом заканчивается, и начинается второй этап, на котором решение задач проводится в обратной последовательности. Регулирующим параметром на этом этапе выступают объемы выпуска продукции 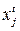 , информация о которых также последовательно передается во все последующие ячейки. При этом оценки
, информация о которых также последовательно передается во все последующие ячейки. При этом оценки  в целевых функциях задач берутся на уровне их значений, найденных на первом этапе. Как видно из алгоритма, в нем сочетаются ценностная (первый этап) и лимитная (второй этап) формы координации задач.
в целевых функциях задач берутся на уровне их значений, найденных на первом этапе. Как видно из алгоритма, в нем сочетаются ценностная (первый этап) и лимитная (второй этап) формы координации задач.
Среди методов блочного программирования наименее исследованы в настоящее время алгоритмы со смешанными вертикально-горизонтальными взаимосвязями, характеризующиеся наиболее сложными процедурами координации подзадач в ходе решения исходной задачи. Между тем данный класс алгоритмов представляет особый интерес не только по чисто вычислительным соображениям. По сравнению с алгоритмами, использующими вертикальную или горизонтальную координацию, декомпозиционные методы со смешанной координацией позволяют наиболее адекватно отразить реальные процессы согласования плановых решений в экономической системе.
|
|
|
При декомпозиционном методе решения задач оптимального планирования необходимость смешанной координации возникает, например, в случае, когда в состав ограничивающих условий исходной задачи входят глобальные ограничения для всех групп переменных (блоков) и ограничения, связывающие между собой отдельные блоки. Такая структура матрицы ограничений характерна, в частности, для задач планирования развития и размещения комплексов взаимосвязанных производств, в которых к глобальным относятся ресурсные ограничения, ограничения по общему выпуску в системе и т. д., а к связывающим – ограничения, отражающие поставки производимой различными ячейками продукции друг другу. В литературе рассмотрены некоторые возможные подходы к решению подобной задачи, основанные на смешанной координации: для вертикальной взаимоувязки – ценностные алгоритмы со стимулированием цен и штрафами и алгоритмы с лимитной формой регулирования; для горизонтальной взаимоувязки задач на нижнем уровне – алгоритм с последовательной координацией.
ГЛАВА 19
Модели и методы оптимизации процессов
в экономике
Критерии оптимальности
Показатель «прибыль»
Если в задачах оптимального планирования в качестве критерия использовать показатель «прибыль», то он может быть использован только при решении статических (объемных) задач на том уровнеиерархии, который характеризует работу предприятия в целом. Такой задачей, прежде всего, является задача формирования годовой производственной программы предприятия.
Пусть Y – годовой план производства.
Полученный при решении задачиобъем прибыли определяется как  . Здесь
. Здесь  – векторы соответствующей размерности, а
– векторы соответствующей размерности, а  – объем прибыли. Использование в динамически задачах (календарного распределения) в качестве критерия этого показателя нецелесообразно по следующимпричинам. Пусть
– объем прибыли. Использование в динамически задачах (календарного распределения) в качестве критерия этого показателя нецелесообразно по следующимпричинам. Пусть  - искомый план
- искомый план  -го календарного периода. Предположим, что требуется найти решение
-го календарного периода. Предположим, что требуется найти решение  , котороебы максимизировало прибыль, то есть
, котороебы максимизировало прибыль, то есть
|
|
|
 .
.
Допустим, что 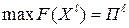 .В силу того, что
.В силу того, что  ,
,  . Это указывает на то, что максимизация прибыли на
. Это указывает на то, что максимизация прибыли на  -м интервале не изменяет общего объема прибыли, полученного от плана
-м интервале не изменяет общего объема прибыли, полученного от плана 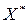 .Следовательно, использование показателя прибыли в динамических задачам нецелесообразно.
.Следовательно, использование показателя прибыли в динамических задачам нецелесообразно.
Показатель «диспропорция загрузки оборудования (ресурсов) »
В статических задачах определения производственного задания на плановый период в качестве критерия используется также показатель «диспропорция загрузки оборудования (ресурсов)». Диспропорция – это сравнительная характеристика отклонений фактического наличия ресурсов от планового для различных видов ресурсов (групп оборудования). Основная цель при формировании планового задания заключается в построении такого плана, который бы обеспечивал наименьшую диспропорцию в использовании ресурсов (оборудования). Требование устранения диспропорций в использовании ресурсов, выступающее в качестве цели, формализованно записывается в следующем виде:
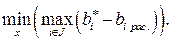
Здесь  – наличный фонд рабочеговремени
– наличный фонд рабочеговремени  -й группы оборудования,
-й группы оборудования,
 – расчетный фонд рабочего времени
– расчетный фонд рабочего времени  -й группы, определяемый по плану;
-й группы, определяемый по плану;
 – выделенное множество групп, каждая из которых состоит из взаимозаменяемого оборудования.
– выделенное множество групп, каждая из которых состоит из взаимозаменяемого оборудования.
Задачи с таким критерием будем называть задачами пропорционального использования ресурсов.
Критерий ритмичности
Основная цель динамических задач планирования заключается в оптимизации режима функционирования производственной системы. Одним из основных показателей оптимального функционирования является ритмичность. Термин ритмичность объединяет два различных понятия: ритмичность производства (работы) и равномерность выпуска продукции.
Критерий «равномерность» будет определяться требованием минимизации максимальных отклонений от фиксированных уровней в каждом из интервалов планируемого периода. Формально критерий записывается в виде:  , где
, где 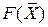 – фиксированный уровень натурального или стоимостного показателя,
– фиксированный уровень натурального или стоимостного показателя,  – реальное значение в
– реальное значение в
 -й период в планируемом объеме.
-й период в планируемом объеме.
|
|
|
Критерий Вальда, Сэвиджа, Гурвица
Впервые прямые методы стохастической оптимизации в экономико-математическом моделировании были применены в 70-х годах. Их преимущества:
· применяются для решения экстремальных задач с негладкими функциями;
· для реализации не требуется знание распределения случайной величины (на каждой итерации достаточно иметь реализацию случайной величины).
Пусть эффективность функционирования системы выражается с помощью функции  , причем
, причем 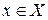 ,
,  . Здесь
. Здесь 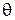 – состояние природы. Тогда задача будет сводиться к выражению
– состояние природы. Тогда задача будет сводиться к выражению 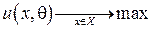 .
.
В этом случае критерий Вальда будет иметь вид:
 .
.
При этом решение дает наибольший эффект в наихудших условиях.
Критерий Сэвиджа:
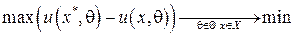 ,
,
где  , другими словами, это критерий минимизации риска в наихудших условиях.
, другими словами, это критерий минимизации риска в наихудших условиях.
Критерии Вальда и Сэвиджа относятся к группе пессимистических критериев.
Критерий Гурвица
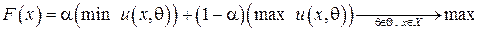
является линейной комбинацией самого пессимистического и оптимистического критериев.
Логическим продолжением критерия Гурвица является учет значений эффекта при всех состояниях природы, взвешенных по вероятности.
Если 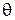 принимает конечное количество значений, и известны вероятности этих значений pi, то решение следует выбирать как
принимает конечное количество значений, и известны вероятности этих значений pi, то решение следует выбирать как

или
 .
.
При этом задача сводится к
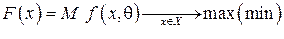 .
.
|
|
|


