 |
Методы итеративного агрегирования
|
|
|
|
Рассмотренные выше итерационные процессы согласования плановых решений в иерархически организованных системах, основанные на методах блочного программирования, позволяют, как правило, уменьшить по количеству уравнений[22] размерность задач, решаемых на каждом уровне иерархии. Однако номенклатура продукции, по которой проводятся расчеты, на всех уровнях предполагается неизменной. В результате центру приходится вести расчеты с той же детализацией показателей, что и на нижних уровнях. Реализация такой процедуры привела бы к перегруженности каналов связи при передаче информации и другим нежелательным последствиям. На практике, как мы знаем, дело обстоит иначе, и на верхних уровнях планирования имеют дело лишь с важнейшими и укрупненными характеристиками.
Учет этих особенностей реальной организации процессов планирования и управления был положен в основу специального класса алгоритмов итеративного согласования решений при разных степенях агрегирования показателей, получивших в литературе название «методы итеративного агрегирования». Одной из первых работ в этой области явились исследования статической модели стоимостного межпродуктового баланса
Л. М. Дудкина и Э. Б. Ершова [17]. Рассмотрим предложенную ими процедуру на следующем примере.
Рассмотрим систему, состоящую из центрального планового органа, задачей которого является координация развития входящих в его подчинение отраслей. Реальный процесс взаимодействия отраслей ведется по детализированной номенклатуре показателей, однако информационно-вычислительные возможности центра (включая каналы связи) позволяют ему оперировать только укрупненной номенклатурой показателей. В целях координации центр предполагает использовать статическую стоимостную модель межотраслевого баланса, число столбцов которого совпадает с количеством отраслей[23].
|
|
|
Обозначим через 
индексы и множество видов продукции в детализированной номенклатуре, 
– индексы и множество видов продукции в укрупненной номенклатуре и будем считать, что отраслям известна классификация всех продуктов детализированной номенклатуры по позициям укрупненной номенклатуры
.
Кроме того, предполагается, что известны 
– норматив затрат 
-го продукта на единицу 
-го продукта[24] и 
– конечное потребление продукции -го вида.
Координированное развитие отраслей требует определения показателей выпуска продукции в детализированной номенклатуре 
, что и является совместной плановой задачей центра и отраслей.
Для проведения расчетов по модели межотраслевого баланса центру необходима информация о коэффициентах затрат продукции в укрупненной номенклатуре. Для этого отрасли, исходя из нормативов и оценочных плановых или отчетных данных о выпуске продукции 
, составляют полуагрегированные нормативы затрат продукции детализированной номенклатуры на единицу продукции укрупненной номенклатуры
(19.1)
а затем по формуле средневзвешенных определяют агрегированные нормативы затрат для продукции в укрупненной номенклатуре
(19.2)
Полученные нормативы передаются в центр, где по модели межотраслевого баланса проводится расчет объемов выпуска продукции в агрегированной номенклатуре
(19.3)
Результаты решения 
поступают на отраслевой уровень, где с помощью полуагрегированных нормативов затрат 
определяются объемы производства продукции детализированной номенклатуры
(19.4)
Центр интересует вопрос: обеспечивает ли подобная процедура расчетов реальную координацию развития отраслей, или являются ли полученные объемы производства 
решением модели межпродуктового баланса
|
|
|
(19.5)
Очевидно, что это условие (соответствующее требованию точного агрегирования[25]) будет выполняться, если использовать в формуле (19.2) решение модели (19.5). Данное решение в начале расчетов было неизвестно, а принятая в (19.1) и (19.2) структура производства продукции планового периода бралась по ориентировочным данным. Полученные таким образом удельные веса отдельных видов продукции детализированной номенклатуры в агрегатах
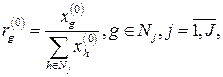(19.6)
могут отличаться от удельных весов, соответствующих решению модели (19.5). Поэтому в общем случае гарантировать выполнение требования точного агрегирования нельзя. Более того, анализ возможных частных случаев показал, что необходимым и достаточным условием точного агрегирования является равенство полуагрегированных коэффициентов затрат продукции отрасли на производство любых конкретных продуктов другой отрасли:
(19.7)
В действительности данное условие не выполняется даже приблизительно, и в пределах каждой отрасли полуагрегированные нормативы существенно разнятся между собой.
Учитывая это, центр предлагает отраслям уточнить значения коэффициентов 
и 
, используя для расчетов в (19.1) и (19.2) полученные ранее решения 
, а затем снова повторяет всю процедуру.
Вычислительная схема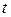 
-й итерации процесса может быть описана следующим образом:
1. определяются нормативы 
:
(19.8)
2. вычисляются нормативы 
:
(19.9)
3. расчитываются объемы производства продукции укрупненной номенклатуры 
:
(19.10)
4. определяются потребности в производстве продукции детализированной номенклатуры 
:
(19.11)
Процесс повторяется до тех пор, пока искомые показатели производства продукции 
и 
, полученные на двух последовательных итерациях, не будут достаточно мало отличаться друг от друга [26].
Собственно, с таким итерационным подходом к операциям агрегирования и дезагрегирования расчетных показателей, включая разработку системы правил, обеспечивающей сходимость процесса к точному решению, и связана идейная сторона методов итеративного агрегирования.
В настоящее время в литературе описан достаточно широкий класс задач, для реализации которых разработаны алгоритмы итеративного агрегирования. К их числу относятся и задачи линейного программирования с блочной структурой ограничений (типа (16.15) – (16.18)).
|
|
|
Вернемся к постановке задачи. Предположим, что координирующий центр оперирует агрегированными характеристиками деятельности хозяйственных ячеек. Представим модель исходной задачи в виде
(19.12)
(19.13)
(19.14)
(19.15)
и рассмотрим следующую процедуру согласования решений в двухуровневой системе «центр – хозяйственные ячейки».
Центр просит хозяйственные ячейки предоставить в его распоряжение обобщенную информацию о предполагаемой деятельности в плановом периоде: агрегированные нормативы затрат ресурсов, величину дохода с учетом стоимости локальных ресурсов, объемы потребления глобальных ресурсов[27]. Для расчета этих показателей ячейки используют ориентировочные данные об объемах будущего производства продукции 
и предполагаемых ценах (оценках) на все виды ресурсов 
. На основе полученных показателей 
центр определяет укрупненный вариант плана выпуска продукции в системе. При этом, учитывая ограниченные возможности для составления плана (по времени, ресурсам и т. д.), он считает целесообразным проводить последовательную эластичную корректировку первоначального проекта. Последнее осуществляется демпфированием процесса планирования с помощью введения в целевую функцию координирующей задачи фиктивных штрафов за «разброс» смежных плановых вариантов.
Модель задачи центра имеет вид
(19.16)
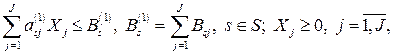(19.17)
где 
и 
– числовые параметры процесса. Квадратичное слагаемое в (19.16) – фиктивный штраф для обеспечения устойчивости процесса.
Полученные из решения задачи (19.16) и (19.17) значения показателей выпуска продукции и оценки ресурсных ограничений 
передаются хозяйственным ячейкам. Кроме того, исходя из полуагрегированных нормативов затрат ресурсов 
, которые рассчитываются ячейками вместе с параметрами 
и варианта плана , центр рекомендует им ориентироваться на потребление общих ресурсов в детализированной номенклатуре в объемах, соответствующих данному варианту 
. При лимитном способе распределения ресурсов это требование соответствует введению в локальную задачу ограничений типа
|
|
|
(19.18)
или с использованием дополнительных переменных 
(19.19)
В случае штрафного стимулирования (который мы будем рассматривать в дальнейшем) данное требование соответствует введению в целевую функцию локальной задачи специальных штрафов за превышение установленных лимитов.
При таком подходе локальная задача, решаемая 
-й хозяйственной ячейкой, может быть представлена в следующем виде:
(19.20)
(19.21)
(19.22)
где 
– параметр процесса.
Поясним смысл целевой функции задачи (19.20). Первое слагаемое представляет собой разность между доходом, получаемым ячейкой, и платой за используемые общие ресурсы. Последние оцениваются по ориентировочным ценам 
, умноженным на оценки задачи центра . Оценки в данном случае играют роль масштабных множителей, показывающих, во сколько раз нужно изменить все оценки ограничений 
-ой группы. Квадратичная часть критерия представляет собой штрафную функцию за отклонение от рекомендуемых центром объемов потребления общих ресурсов. Рассмотрим структуру и действие данного штрафного слагаемого. Обозначим для краткости через 
оценку 
-го ресурса при решении локальной задачи и через 
– экономию 
или перерасход 
ячейкой -го ресурса по сравнению с рекомендациями центра
Тогда, прибавив к (19.20) постоянное слагаемое 
(стоимость объемов ресурсов, выделяемых центром -й ячейке), целевую функцию локальной задачи можно представить в виде
(19.23)
Найдем частный экстремум функции (19.23) по 
:
(19.24)
Подставив найденное значение 
в (19.23), представим целевую функцию локальной задачи в виде
, (19.25)
где
Обратимся к графику функции 
, приведенному на рис. 19.1.
|
|
|
Рисунок 19.1 График целевой функции
Как видно из графика, при перерасходе ресурса на ячейку накладывается штраф, причем штрафные ставки увеличиваются с ростом перерасхода ( – выпуклая вверх функция на интервале 
и 
на полуинтервале 
), а при экономии ячейка поощряется по убывающим ставкам, причем, начиная с определенного момента 
, дополнительные выплаты за экономию берутся в фиксированных размерах.
Подобное стимулирующее штрафование обеспечивает гибкое воздействие центра на хозяйственные ячейки с целью их ориентации на рекомендуемые объемы потребления общих ресурсов.
Решение локальных задач позволяет ячейкам установить новый вариант производства продукции 
и оценок на все виды ресурсов 
. Однако оценки по общим ресурсам 
у различных ячеек (в общем случае) не совпадают и, характеризуя локальную эффективность использования ресурсов, не дают представления об их полезности для системы в целом. Поэтому центр проводит предварительную корректировку оценок глобальных ресурсов, учитывая их общую экономию или перерасход:
|
|
|
(19.26)
где – параметр процесса, а нижний индекс 
означает, что отрицательное число заменяется нулем[28].
Смысл формулы (19.26) достаточно прозрачен. При перерасходе
-го ресурса в целом по системе его оценка увеличивается, причем приращение оценки пропорционально величине перерасхода 
. При экономии ресурса его оценка уменьшается на величину, пропорциональную недоиспользованному остатку 
. Если новая оценка оказалась отрицательной, она заменяется нулем[29].
Проявляя определенную осторожность при пересмотре расчетных показателей плана, центр рекомендует хозяйственным ячейкам построить новый вариант плана как компромисс между предварительным проектом 
и полученным решением 
:
где 
– параметр процесса.
Полученный вариант плана 
используется центром для организации нового цикла расчетов.
Описанная процедура расчетов соответствует одному из широко освещенных в литературе алгоритмов итеративного агрегирования для задач линейного программирования с блочной структурой ограничивающих условий. Алгоритм имеет следующую вычислительную схему (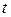 -я итерация):
1. расчет полуагрегированных и агрегированных показателей:
a. полуагрегированных нормативов затрат ресурсов:
(19.28)
b. агрегированных нормативов затрат ресурсов:
(19.29)
c. агрегированных показателей целевой функции:
(19.30)
d. агрегированных показателей наличия общих ресурсов:
(19.31)
2. решение агрегированной задачи
(19.32)
, (19.33)
где – параметр процесса, 
.
Решение прямой задачи (19.32) и (19.33) – 
, двойственной – 
3. Решение локальных задач 
:
(19.34)
(19.35)
где – параметр процесса.
Решение прямой задачи – 
, двойственной – 
4. Вычисление оценок на общие ресурсы (предварительное):
(19.36)
где 
– параметр процесса;
5. вычисление очередного приближения к решению:
(19.37)
где – параметр процесса.
Строгого доказательства сходимости алгоритма (19.28) – (19.37) в настоящее время не существует. В работах можно встретить доказательство теоремы об оптимальности неподвижной точки процесса, что при условии достаточных экспериментальных подтверждений предельной сходимости алгоритма позволяет говорить о его сходимости к решению исходной задачи (19.12) – (19.15).
|
|
|
