 |
Модели экономического равновесия
|
|
|
|
Хозяйственные объекты с присущими каждому из них индивидуальными функциями, в соответствии с которыми они организовывают свое поведение в пределах имеющихся возможностей, будем называть активными, а модели, изучающие взаимодействие таких объектов, – поведенческими. С формальных позиций оптимальные экономические модели со сложной структурой в ряде случаев можно интерпретировать как поведенческие. Если считать, что глобальный критерий аддитивен и задается на множестве интересов хозяйственных ячеек, то локальные критерии оптимальности в моделях последних можно рассматривать как индивидуальные целевые функции. Согласно им организовывается поведение ячеек, которые в рамках существующих внешних условий самостоятельно определяют свою наилучшую внутреннюю структуру.
Однако принимаемая в декомпозиционных процедурах планирования система допущений, связанная с оценкой локальных решений лишь по отношению к экзогенно заданному глобальному критерию, а также с предположением, что использование основных регулирующих параметров хозяйственного механизма автоматически обеспечит «оптимальность» выбираемых решений с позиций интересов соответствующих ячеек, представляется достаточно жесткой. Она не позволяет отразить в достаточной мере все аспекты реального процесса функционирования экономической системы и, в частности, те из них, которые связаны с наличием у хозяйственных ячеек собственных интересов, определяющих их поведение на этапе реализации плана, а также при принятии децентрализованных решений. Именно на эти стороны функционирования системы в целом и ее отдельных подразделений делается основной упор в так называемых «моделях экономического равновесия»[30].
|
|
|
В моделях равновесия предполагается, что задано множество участников экономической системы. Каждый из них имеет свою индивидуальную целевую функцию, которую он стремится оптимизировать, и область производственных возможностей по выпуску продуктов и услуг. Функционирование системы рассматривается как процесс взаимодействия ее участников, принимающих с учетом внешних требований самостоятельные решения относительно своей деятельности и вступающих в хозяйственные отношения по поводу обмена и распределения продукции с другими участниками.
При исследовании поведения системы с помощью моделей равновесия возникают две центральные проблемы. Во-первых, нахождение финального состояния (траектории), к которому приходит система в процессе своего функционирования. Во-вторых, решение вопроса о допустимости самодействия в этом процессе каждого отдельного участника, если последний обладает весьма «сжатой» информацией о поведении остальных участников системы.
Данные проблемы, очевидно, возникают при любом подходе к исследованию процессов функционирования экономики и в рамках каждого из них решаются по-разному. Так, в оптимизационных моделях со сложной структурой задача нахождения финального состояния, к которому стремятся участники системы, заключается в выявлении глобального критерия оптимальности и его экстремального значения при имеющихся ресурсах. В моделях экономического равновесия нет явно выраженного глобального критерия. Его поиск заменяется другой задачей, связанной с формированием механизма отношений, в которые вступают оптимизирующие свое поведение участники.
Попытаемся изложить основные исходные принципы, «закладываемые» в механизм экономического взаимодействия, в такой последовательности, чтобы введение каждого из них влекло за собой соответствующее сужение области поиска финального состояния (траектории) системы.
|
|
|
Рассмотрим хозяйственную систему, состоящую из 
участников (ячеек) с планами выпуска продуктов 
, индивидуальными целевыми функциями 
и областями производственных возможностей 
. Обозначим через 
план системы как композицию планов отдельных участников.
С учетом общесистемных ограничений, определяющих область допустимых решений 
на множестве возможных планов развития хозяйственных ячеек, может быть составлена задача векторной оптимизации с целевой функцией 
и совокупностью ограничивающих условий 
, решение которой, как отмечалось выше, позволяет найти эффективные (оптимальные по Парето) варианты. Последние характеризуются тем, что ни один из участников, действуя самостоятельно или совместно с другими участниками, не может улучшить своего положения так, чтобы при этом не ухудшилось положение какого-либо участника системы.
Определение множества эффективных планов 
значительно сужает область возможного финального состояния (траектории) системы. Принадлежность к этому множеству является очевидным требованием к принятию согласованных решений в системе, состоящей из нескольких экономически самостоятельных участников. Но одного его еще недостаточно для обеспечения заинтересованности ячеек в совместной деятельности. Разумным основанием для этого является возможность такой процедуры обмена и распределения производимых продуктов и услуг между участниками, которая приводит к повышению значения их индивидуальных целевых функций по сравнению с обособленным функционированием.
Различные эффективные планы неодинаково выгодны для разных участников. Не исключена и возможность того, что кто-либо из них, действуя самостоятельно или в коалиции с другими, сможет добиться лучших для себя результатов. «Отсечение» подобных ситуаций связано с исследованием механизмов экономического взаимодействия в системе с переменным составом участников и введением понятия «ядро системы».
Ядро системы 
представляет собой совокупность допустимых решений, ни одно из которых не может быть улучшено, в смысле оптимума по Парето, при выделении из хозяйственной системы любой коалиции ее участников. Другими словами, если 
– допустимое решение и 
, то участники коалиции 
не могут получить значения целевых функций 
для всех 
и хотя бы один из них – 
.
|
|
|
Ядро – множество более узкое, чем множество эффективных точек. Всякий план, принадлежащий ядру, является оптимальным по Парето 
, причем обратное утверждение в общем случае неверно. Совпадение этих множеств 
означает, что участники хозяйственной системы, в принципе, экономически заинтересованы в реализации любого плана, эффективного для системы в целом. Чем более жесткие внешние требования накладываются на деятельность отдельных участников, чем теснее взаимосвязи между ними, тем меньше различия между множеством оптимальных по Парето вариантов и ядром системы.
Обратимся к приведенному на рис. 19.2 примеру для системы, состоящей из двух участников. На нем изображено множество всех значений индивидуальных целевых функций 
и 
на области допустимых решений. Часть границы этого множества – ломаная 
– определяет совокупность значений функций, соответствующих оптимальным по Парето вариантам. Значения 
и 
– экстремумы целевых функций участников при их изолированном функционировании. Участники заинтересованы в совместной деятельности, поскольку она может обеспечить получение более высоких результатов по сравнению с и . Соответствующие значения целевых функций образуют ломаную 
, определяющую варианты из ядра системы. Линии 
и 
характеризуют множества оптимальных по Парето планов, которые, однако, не принадлежат ядру. С позиций своих экономических интересов первый из участников будет выступать против реализации вариантов со значениями 
, для второго неприемлемы варианты с 
.
Рисунок 19.2 Область допустимых решений для двух участников
Дальнейшее нахождение финального состояния или траектории системы на множестве допустимых планов, образующих ядро, предполагает введение конкретных параметров и правил регулирования отношений между участниками. В зависимости от особенностей исследуемого процесса взаимодействия хозяйственных ячеек набор этих параметров может быть различным.
|
|
|
Общей характерной чертой моделей экономического равновесия является использование в них ценностной формы соизмерения затрат и результатов деятельности каждого участника (путем введения «бюджетных» ограничений) и регулирования их хозяйственных взаимосвязей.
Рассмотрим пример системы, состоящей из производителей 
и 
потребителей 
, 
видов продукции 
и некоторого ценообразующего органа, задачей которого является выработка таких цен на производимые товары, при которых предложение этих товаров уравновешивает спрос на них[31]. При фиксированных ценах (вектор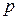 
)[32] каждый производитель решает задачу максимизации дохода от своей деятельности:
(19.38)
где 
– множество допустимых производственных планов (векторов чистого выпуска) 
производителя.
Решение задачи (19.38) – вектор 
– назовем предложением производителя при данном векторе цен.
Потребитель с индексом 
описывается моделью рационального поведения. Решаемая им задача заключается в максимизации функции полезности 
на множестве допустимых векторов потребления 
[33] с учетом соответствующих бюджетных ограничений
, (19.39)
где 
– начальный запас товаров у потребителя;
– коэффициенты долевого участия 
-гo потребителя в доходах -го производителя.
Решение задачи (19.39) – вектор 
– является вектором спроса потребителя при заданных ценах .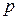
Задачей центра является минимизация «рассогласования» в системе между совокупным спросом потребителей и совокупным предложением производителей. Если 
– совокупный спрос и 
– совокупное предложение, то величина 
выражает данное «рассогласование», то есть избыточный спрос потребителей. В этом случае задача центра имеет вид
(19.40)
где 
– множество нормированных цен.
Последовательно варьируя значения регулирующих параметров в системе (то есть цены) и используя информацию о поведении производителей и потребителей (величине предложения и спроса), центр проводит их итеративное уточнение, обеспечивающее выход системы в состояние равновесия. Под последним понимается состояние, в котором ни одному из участников системы (включая центр) не выгодно менять свое поведение при фиксированном поведении других участников. С формальной точки зрения для хозяйственной системы, описываемой совокупностью моделей (19.38) – (19.40), состояние равновесия задается набором векторов 
, в котором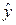 
является решением задачи (19.38) при ценах 
; 
является решением задачи (19.39) при ценах ; 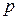является решением задачи (19.40) при значении вектора избыточного спроса 
.
В общем случае, когда композиция планов отдельных участников 
должна удовлетворять некоторым общесистемным ограничениям, вектор цен 
будем называть равновесным, если среди оптимальных планов участников, рассчитанных при этих ценах 
, найдутся такие, которые образуют допустимый план системы в целом. Другими словами, множества содержат такие планы 
, что
|
|
|
где – множество допустимых планов системы.
Совокупность векторов 
называется состоянием (траекторией) равновесия, если
(19.41)
и
Найденное состояние (траектория) равновесия представляет собой согласованный план совместной деятельности хозяйственных ячеек в рамках установленных принципов экономического взаимодействия, регламентирующих поведение отдельных участников и их отношения в системе. Следует, однако, учитывать, что изменение этих принципов, в частности принципов обмена и распределения, может повлечь за собой изменение равновесного состояния системы.
Существование решения в моделях экономического равновесия, как правило, удается доказать при весьма жестких предпосылках. Стандартными являются предположения о выпуклости множеств допустимых решений и вогнутости целевых функций, соответствующие условиям выпуклого программирования. Часто используется гипотеза о ненасыщаемости спроса хотя бы у части потребителей. В исследованиях, посвященных теоремам существования, для моделей равновесия обычно формируется совокупность достаточных условий, некоторые из которых могут и не быть необходимыми.
Модели хозяйственных систем, описывающие взаимообусловленное поведение участников с особыми интересами, получили широкое развитие в исследованиях представителей зарубежной математической экономии. Наибольшую известность среди них получила модель конкурентного экономического равновесия К. Эрроу–Г. Дебре–Л. Мак-Кензи.
Уместен вопрос: а не противоречит ли сам принцип построения моделей экономического равновесия и основанных на них композиционных процедур планирования реальному механизму функционирования плановой экономики, приоритетности общегосударственных интересов, требованию рационального подхода к принятию плановых решений? Пытаясь подчеркнуть отличия моделей композиционного планирования развития экономики от игровых схем рынка, их авторы обычно делают упор на наличие в композиционных схемах специальной модели центра. Думается, однако, что суть дела заключается не в этом, тем более что, в принципе, наличие специальных моделей для «государственного сектора» вполне допустимо и в схемах рыночной экономики.
В действительности все зависит от того, какой тип производственных отношений, механизма обмена и распределения в экономической системе «закладывается» в композиционную схему, какие цели и интересы системы отражает модель центра, как строятся экономические отношения между центром и прочими участниками, какие экзогенные требования накладываются на всю систему в целом, какими рамками и правилами регламентируется экономическая самостоятельность отдельных участников. Если в этих составляющих конструкции композиционной схемы заложен принцип общеэкономического подхода к выбору оптимума, то реализация этого требования (как следствие) будет иметь место и в случае построения процедуры разработки плана по данной схеме.
Рассмотрим теперь на упрощенном примере процедуру формирования плана в экономической системе, состоящей из ряда локальных хозяйственных ячеек и центрального планового органа, которая реализуется в виде следующей игровой задачи.
Пусть 
– план деятельности -й ячейки , удовлетворяющий некоторым локальным условиям (например, для производственных объединений это условия технологической допустимости решений, для экономического района – лимитные ограничения на использование природных и трудовых ресурсов и т. д.), и – множество локально допустимых планов этой ячейки. Кроме локальных условий, выбор плана ячейкой зависит от стратегии центра (закрепим за ним индекс 0) и планов других участников игры 
. Обозначим через 
множество планов -й ячейки, удовлетворяющих таким внешним условиям. Тогда множество допустимых планов 
локальной ячейки можно представить в виде
(19.42)
Задача, решаемая -й ячейкой, заключается в оптимизации функции выигрыша 
, отражающей собственные интересы этой ячейки на множестве допустимых решений .
В процессе функционирования системы центр решает двоякую задачу. С одной стороны, центр стремится к выработке плана, согласованного с точки зрения интересов отдельных участников, что обеспечивает его успешную реализацию. Данные цели центра отражаются как в его функции выигрыша, так и во влиянии избираемой им стратегии на поведение локальных ячеек. С другой стороны, центр как ячейка институциональной структуры, выражающая интересы системы в целом, обладает определенными собственными интересами, не сводящимися к интересам локальных ячеек и требованиям их согласования (например, в области внешней политики, обороны, фундаментальных научных исследований и т. д.). Соответственно, функцию выигрыша центра 
в задаче представим в виде
(19.43)
где 
отражает арбитражные, а 
– неарбитражные интересы центра[34].
Поскольку реализация неарбитражных целей центра зависит от результатов деятельности участников системы, в рамках рассматриваемой задачи можно считать, что 
. Первое слагаемое в (19.43) представим в виде штрафной функции, характеризующей оценку центром планов локальных производственных ячеек:
(19.44)
где 
– множество локальных производственных ячеек в системе;
– компонента стратегии центра 
, относящаяся к его оценке деятельности -й ячейки;
– неположительная функция для всех 
, причем 
в случае приемлемости плана -й ячейки (будем считать, что тогда 
) и быстро убывает при отклонении от 
.
Функция выигрыша центра определена на множестве 
, причем в качестве «локальных» условий, определяющих множество 
, рассматриваются факторы среды, внешней по отношению к моделируемой экономической системе.
Поскольку в действительности часть компонентов целей центра и локальных ячеек может не поддаваться строгой количественной оценке (например, в сфере внешней политики, экологии и т. д.), их учет в модели осуществляется путем экзогенной коррекции множеств и . Скажем, при формировании множества такая коррекция заключается в учете отвлечения ресурсов для выполнения внешнеполитических, экологических и других функций в фиксированных объемах. Аналогичное уточнение может приводиться и по отношению к множествам локально допустимых планов некоторых ячеек, например, экономических районов. Коррекция множеств и , влияя на множества допустимых планов 
и и тем самым на выбор стратегий участниками системы, позволяет учесть в процессе выработки плана значительное число факторов, не поддающихся внутримодельному определению.
Однако среди них есть и такие, которые необходимо учитывать непосредственно при задании множеств . Это относится, в частности, к ограничениям, связанным с процессами движения населения. Данные процессы, оказывая влияние на формирование множеств , в свою очередь, существенно зависят от принятых ячейками системы планов 
. В связи с этим в модель вводится дополнительный 
участник, персонифицирующий такие процессы поведения системы, которые не поддаются отображению в форме явно заданной функции выигрыша. Соответствующая коррекция множеств допустимых планов осуществляется в виде представления каждого из множеств 
как зависящего не только от , но и от 
стратегии, избираемой данным дополнительным участником. Его роль в игре уже не сводится к нормативному выбору стратегии из некоторого множества допустимых решений, а предполагает прогноз такого выбора 
, который сделало бы население при условиях, фиксируемых планами 
участников системы и состоянием внешней среды.
Специфика данного дополнительного участника, проявляющаяся в описании его возможностей и предпочтений в нестандартной форме, делает необходимым итеративную организацию процесса решения игры. При некоторых дополнительных предположениях о роли -го участника рассмотренная игра может быть представлена как частный случай реализации системы моделей композиционного планирования, для которой доказано существование ситуации равновесия в случае выпуклости множеств допустимых планов и вогнутости целевых функций в задачах центра и локальных ячеек.
|
|
|
