 |
Задачи оптимального управления
|
|
|
|
Традиционно со времен Эйлера физика и механика, а затем и практика машиностроения были основными «поставщиками» вариационных задач. Однако в конце 50-х годов новое поле деятельности было открыто не традиционными интересами чистой математики, а рутинной инженерной практикой.
Вывод на орбиту некоторого груза требовал огромных затрат энергии. Поэтому весьма актуальной стала проблема выбора такой траектории стартового участка космической ракеты, при движении вдоль которой с той же затратой топлива можно было бы вывести на орбиту лишний килограмм полезного груза.
Первым, кто понял суть этой проблемы, был Д.Е. Охоцимский. Еще в 1946 году, будучи студентом, он опубликовал посвященную ей работу. Оказалось, что задачи выбора оптимальной траектории выходят за рамки классического анализа (того вариационного исчисления, которое было создано Эйлером и Лагранжем) и требуют разработки новых математических подходов. И он уже содержался в знаменитой статье Охоцимского. Но решающий шаг сделал не он.
О статье Охоцимского помнят только отдельные специалисты. Дело в том, что лет через пять после этой работы Л.С. Понтрягин опубликовал свой принцип максимума. Им была предложена чрезвычайно простая и элегантная конструкция, позволяющая сводить эти нестандартные задачи анализа к краевым задачам для обыкновенных дифференциальных уравнений – задачам трудным, но все же решаемым классическими методами численного анализа.
Так, например, если движение ракеты описывается ее координатами  и
и 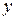 , проекциями вектора скорости на координатные оси
, проекциями вектора скорости на координатные оси  и
и  , массой
, массой  , величиной тяги
, величиной тяги  и углом
и углом  между направлением тяги и осью
между направлением тяги и осью  , то управление траекторией ракеты осуществляется за счет регулирования величины и направления силы тяги двигателя. Величины
, то управление траекторией ракеты осуществляется за счет регулирования величины и направления силы тяги двигателя. Величины  и
и  – это управляющие параметры, через
– это управляющие параметры, через 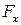 и
и  обозначены суммарные проекции силы тяжести, сопротивления атмосферы и т. д.
обозначены суммарные проекции силы тяжести, сопротивления атмосферы и т. д.
|
|
|
В технических задачах обычно возникает вопрос об отыскании наиболее экономной программы работы модели. В случае движения ракеты чем меньшее количество топлива будет израсходовано, тем более экономичной будет программа. Это означает, что управление  и
и  должно быть выбрано из условия минимума интеграла вида:
должно быть выбрано из условия минимума интеграла вида:
 .
.
Функция 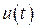 , которая удовлетворяет всем ограничениям и дает минимальное значение интегралу
, которая удовлетворяет всем ограничениям и дает минимальное значение интегралу  , называется оптимальным управлением.
, называется оптимальным управлением.
Таким образом, состояние объекта задается в каждый момент времени числами 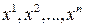 , которые называются фазовыми координатами объекта. Движение объекта (с математической точки зрения) заключается в том, что его состояние с течением времени изменяется, то есть
, которые называются фазовыми координатами объекта. Движение объекта (с математической точки зрения) заключается в том, что его состояние с течением времени изменяется, то есть 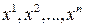 являются переменными величинами. Это движение объекта происходит не самопроизвольно – им можно управлять. Для этого объект снабжен «рулями», положение которых характеризуется в каждый момент времени
являются переменными величинами. Это движение объекта происходит не самопроизвольно – им можно управлять. Для этого объект снабжен «рулями», положение которых характеризуется в каждый момент времени  числами
числами 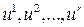 . Эти числа называются управляющими параметрами. Рулями можно «манипулировать» – менять с течением времени управляющие параметры
. Эти числа называются управляющими параметрами. Рулями можно «манипулировать» – менять с течением времени управляющие параметры 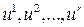 по своему желанию. Иначе говоря, мы можем выбрать функции
по своему желанию. Иначе говоря, мы можем выбрать функции  , которые описывают изменение управляющих параметров с течением времени. Что же касается функций
, которые описывают изменение управляющих параметров с течением времени. Что же касается функций  , то они уже не в полной мере зависят от нашего желания. Мы будем предполагать, что, зная фазовое состояние объекта в начальный момент времени
, то они уже не в полной мере зависят от нашего желания. Мы будем предполагать, что, зная фазовое состояние объекта в начальный момент времени  и выбрав управляющие функции
и выбрав управляющие функции  , мы сможем математически точно рассчитать поведение объекта для всех
, мы сможем математически точно рассчитать поведение объекта для всех 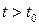 , то есть сможем найти функции
, то есть сможем найти функции  , характеризующие изменение фазовых координат с течением времени. Таким образом, на изменение фазовых координат мы можем воздействовать в той или иной мере, выбирая по своему усмотрению управляющие функции
, характеризующие изменение фазовых координат с течением времени. Таким образом, на изменение фазовых координат мы можем воздействовать в той или иной мере, выбирая по своему усмотрению управляющие функции  .
.
|
|
|
Величины  удобно считать координатами некоторого вектора
удобно считать координатами некоторого вектора  , который также называют управляющим параметром. Точно так же величины
, который также называют управляющим параметром. Точно так же величины 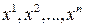 удобно рассматривать как координаты некоторого вектора (или точки)
удобно рассматривать как координаты некоторого вектора (или точки)  . Эту точку называют фазовым состоянием объекта. Каждое фазовое состояние
. Эту точку называют фазовым состоянием объекта. Каждое фазовое состояние  является точкой
является точкой  -мерного пространства с координатами
-мерного пространства с координатами 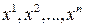 . Это
. Это  -мерное пространство называют фазовым пространством рассматриваемого объекта.
-мерное пространство называют фазовым пространством рассматриваемого объекта.
Чтобы полностью задать движение объекта, надо задать его фазовое состояние в начальный момент времени  и выбрать управляющие функции
и выбрать управляющие функции 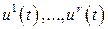 , то есть выбрать векторную функцию
, то есть выбрать векторную функцию
 .
.
Эту функцию мы будем называть управлением. Задание начального фазового состояния  и управления
и управления 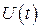 однозначно определяет дальнейшее движение объекта. Это движение заключается в том, что фазовая точка
однозначно определяет дальнейшее движение объекта. Это движение заключается в том, что фазовая точка  , изображающая состояние объекта, с течением времени перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движения объекта. Пару векторных функций
, изображающая состояние объекта, с течением времени перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движения объекта. Пару векторных функций  , то есть управление
, то есть управление 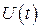 и соответствующую фазовую траекторию
и соответствующую фазовую траекторию  , мы будем называть в дальнейшем процессом управления.
, мы будем называть в дальнейшем процессом управления.
Итак, получаем следующее описание.
Состояние управляемого объекта в каждый момент времени характеризуется фазовой точкой  . На движение объекта можно воздействовать при помощи управляющего параметра
. На движение объекта можно воздействовать при помощи управляющего параметра  . Изменение величин
. Изменение величин 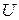 и
и  с течением времени мы называем процессом управления; процесс
с течением времени мы называем процессом управления; процесс  состоит из управления
состоит из управления 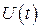 и фазовой траектории
и фазовой траектории  . Процесс полностью определен, если задано управление
. Процесс полностью определен, если задано управление 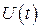 и начальное фазовое состояние
и начальное фазовое состояние  .
.
Часто встречается следующая задача, связанная с управляемыми объектами.
В начальный момент времени  объект находится в фазовом состоянии
объект находится в фазовом состоянии  . Требуется выбрать такое управление
. Требуется выбрать такое управление 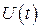 , которое переведет объект в заранее заданное конечное фазовое состояние
, которое переведет объект в заранее заданное конечное фазовое состояние 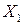 (отличное от
(отличное от  ). При этом обычно требуется, чтобы процесс перехода из начального фазового состояния
). При этом обычно требуется, чтобы процесс перехода из начального фазового состояния  в требуемое конечное состояние
в требуемое конечное состояние 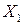 был в определенном смысле «наилучшим», например, чтобы время перехода было наименьшим или чтобы энергия, затраченная в течение переходного процесса, была минимальной и т. д. Такой «наилучший» процесс перехода называется оптимальным процессом. Если речь идет о наименьшем времени перехода, то такие процессы называются оптимальными в смысле быстродействия. Иначе говоря, процесс, в результате которого объект переходит из точки
был в определенном смысле «наилучшим», например, чтобы время перехода было наименьшим или чтобы энергия, затраченная в течение переходного процесса, была минимальной и т. д. Такой «наилучший» процесс перехода называется оптимальным процессом. Если речь идет о наименьшем времени перехода, то такие процессы называются оптимальными в смысле быстродействия. Иначе говоря, процесс, в результате которого объект переходит из точки  в точку
в точку 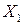 , называется оптимальным в смысле быстродействия, если не существует процесса, переводящего объект из
, называется оптимальным в смысле быстродействия, если не существует процесса, переводящего объект из  в
в 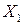 за меньшее время (
за меньшее время ( ).
).
|
|
|
|
|
|


