 |
Общая постановка принципа максимума Понтрягина
|
|
|
|
Рассмотрим систему дифференциальных уравнений:
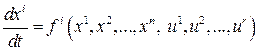, (19.45)
где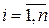 
.
Она описывает поведение некоторого объекта во времени. В момент времени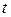 
переменные 
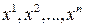могут означать координаты точек, скорости и т. д.
Управление характеризуется точками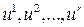 
, в качестве которых могут выступать количество подаваемого в двигатель топлива, температура и т. д. Очевидно, что эти параметры удовлетворяют некоторым ограничениям. Предполагается, что функции 
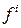непрерывны по совокупности всех аргументов и непрерывно дифференцируемы по совокупности фазовых координат .
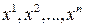При заданных начальных условиях система (19.45) имеет единственное решение, если задать функции 
со значениями из 
.
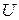Пусть выбрано допустимое управление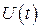 
и получена фазовая траектория 
с начальным условием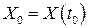 
.
Тогда система
, 
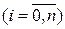
имеет единственное решение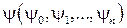 
при любых начальных условиях 
.
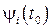С помощью полученных функций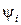 
строится функция Гамильтона
.
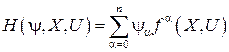Для оптимальности управления 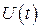и траектории необходимо существование такой ненулевой непрерывной вектор-функции 
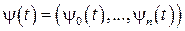, соответствующей функциям 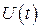и , что при любом (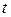
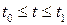) функция 
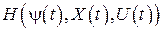переменного 
достигает максимума в точке 
.
В конечный момент времени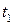 
, 
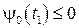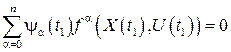. (19.46)
Кроме того, если 
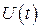, , удовлетворяют системам (19.45) и (19.46), то функци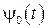и 
и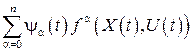 
являются постоянными, и в условии (19.46) точку 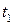можно заменить любой другой.
Для оптимальных по быстродействию управления 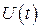и траектории необходимо существование такой ненулевой непрерывной вектор-функции 
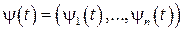, соответствующей функциям 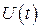и , что для всех 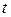(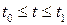) функция
переменного достигает максимума в точке .
В конечный момент времени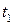
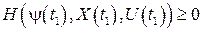. (19.47)
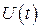Если величины , и удовлетворяют системе
, 
, 
,
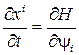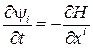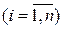и выполнено условие максимума, то функция 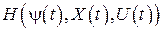переменного 
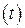постоянна, и неравенство (19.47) можно проверять при любом другом значении ().
|
|
|
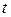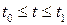Принцип максимума позволяет из всех фазовых траекторий, начинающихся в точке 
и заканчивающихся в требуемой конечной точке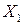 
, и соответствующих им управлений выделить лишь те, которые удовлетворяют всем сформулированным условиям.
Следовательно, имеются лишь отдельные фазовые траектории, удовлетворяющие условиям. И только эти отдельные траектории могут оказаться оптимальными, так как указанные в принципе максимума условия необходимы для оптимальности. Если условиям удовлетворяет только одна фазовая траектория, то можно надеяться, что найденная фазовая траектория и является оптимальной.
Приложения принципа максимума Понтрягина
Рассмотрим два примера использования принципа максимума Понтрягина на практике, которые были разработаны на основе классических задач: навигационной задачи Цермело и простейшей задачи регулирования по быстродействию.
Навигационная задача Цермело: в стационарном поле скоростей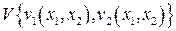 
, где 
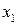и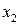 
– прямоугольные декартовы координаты, движется точка с постоянной по величине скоростью 
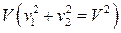. Дано: 
, 
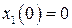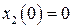; требуется минимизировать время
,
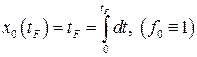необходимое для достижения заданной конечной точки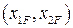 
посредством выбора 
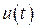угла между направлением скорости 
точки и осью .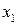
Уравнения состояния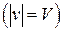 
:
.
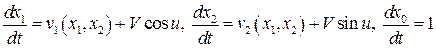Отсюда
,
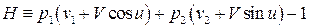где принято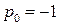 
.
Для максимума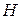 
необходимо, чтобы выполнялось равенство
;
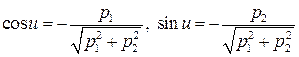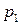и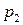 
должны удовлетворять сопряженным уравнениям
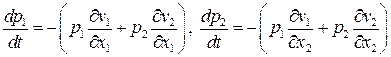
и
.
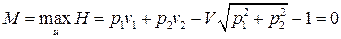Если, в частност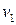и, 
и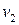 
постоянны, то таковы же 
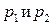; их значения вместе с 
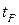удовлетворяют условиям
.
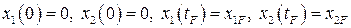Простейшая задача регулирования по быстродействию: даны
– объем производимой продукции,
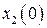– скорость реализации продукции,
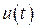– изменение скорости реализации продукции
и уравнения состояния
, (то есть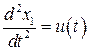 
).
Требуется минимизировать время
, (
),
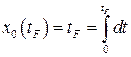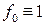необходимое для достижения заданного конечного состояния
|
|
|
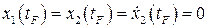
посредством оптимального управления такого, что
.
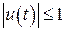Максимизация гамильтониана
(
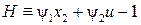
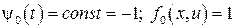– задача на быстродействие) при условии 
приводит к управлению
и
,
так что
.
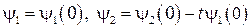Оптимальные траектории в плоскости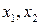 
являются дугами парабол, соответствующих 
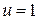и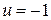 
. Эти дуги пересекают «кривую переключений», соответствующую 
, и каждая траектория продолжается к началу координат вдоль этой кривой.
Каждая траектория зависит от параметров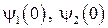 
, которые должны выбираться так, чтобы выполнялись заданные граничные условия 
.
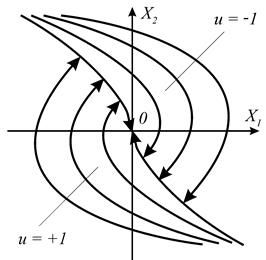
Рисунок 19.3 Фазовый портрет в окрестности точки равновесия
Таким образом, область применения принципа максимума Понтрягина распространяется не только на физические процессы, имеющие место в технике. Он может использоваться также в экономике для решения целого ряда задач оптимального управления.
|
|
|
