 |
Московский государственный университет
|
|
|
|
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. М. В. ЛОМОНОСОВА
ХИМИЧЕСКИЙ ФАКУЛЬТЕТ
В. Г. Чирский
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
(4 СЕМЕСТР)
МОСКВА 2022
Предлагаемая Вашему вниманию брошюра содержит курс лекций В. Г. Чирского по математическому анализу, читаемый в 4 семестре для общего потока химического факультета.
Материал, данный в этой разработке, соответствует экзаменационным билетам. В конце разработки содержатся два полезных приложения, содержание которых позволит лучше понять теоретический курс и быстрее вычислять часто встречающиеся интегралы.
Оглавление
Глава 1. Двойные интегралы
§1. Определение двойного интеграла и критерий интегрируемости
1. 1. Определение двойного интеграла
1. 2 Критерий интегрируемости
§2. Свойства двойных интегралов
3. Вычисление двойного интеграла сведением к повторному
§4. Замена переменных в двойном интеграле
§5. Переход к полярным координатам. Вычисление 
Глава 2. Тройные интегралы
Глава 3. Криволинейные интегралы
§1. Криволинейные интегралы первого типа
§2. Криволинейные интегралы второго типа
§3. Формула Грина
§4. Независимость криволинейного интеграла от формы пути интегрирования
§5. Связь с вопросом о полном дифференциале
Глава 4. Поверхностные интегралы
§1. Площадь поверхности, заданной явным уравнением
§2. Площадь поверхности, заданной параметрическими уравнениями
§3. Поверхностные интегралы 1-го типа
§4. Поверхностные интегралы 2-го типа
4. 1. Понятие стороны поверхности
4. 2. Поверхностные интегралы 2-го типа
§5. Формула Остроградского-Гаусса
§6. ФормулаСтокса
|
|
|
Глава 5. Приложения кратных, криволинейных и поверхностных интегралов. Элементы теории поля
§1. Скалярное и векторное поле
§2. Производная скалярного поля по направлению. Градиент скалярного поля §3. Поток вектора через поверхность. Дивергенция векторного поля. Векторная формулировка теоремы Остроградского-Гаусса §4. Соленоидальное поле §5. Циркуляция, ротор. Векторная формулировка теоремы Стокса Приложение 1. Введение в теорию дифференциальных форм Приложение 2. Эйлеровы интегралы
Глава 1. Двойные интегралы
§1. Определение двойного интеграла и критерий интегрируемости
1. 1. Определение двойного интеграла
Мы будем рассматривать функции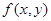 
, определённые на квадрируемом (то есть имеющем площадь) множестве 
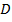. Практически всегда 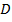представляет собой фигуру, ограниченную кусочно-гладкой кривой, или конечное объединение таких фигур. Далее, говоря о квадрируемом множестве, мы ограничиваемся рассмотрением именно таких множеств.
Если вспомнить теорию определённого интеграла, то мы начали её изложение с понятия разбиения 
отрезка 
. По аналогии, определим разбиение 
квадрируемого множества 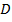, как представление множества 
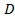в виде объединения конечного числа квадрируемых частей, 
.
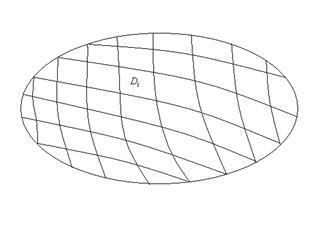
Можно считать, что разбиение 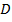на части 
также осуществляется с помощью спрямляемых(т. е. имеющих длину) кривых, то есть все 
также являются фигурами с кусочно-гладкими границами, либо конечными объединениями таких фигур.
В одномерном случае мы рассматривали длины частей разбиения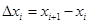 
. В двумерном случае обобщением понятия длины 
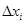будет площадь . Однако нам потребуется также понятие диаметра множества 
. Эта величина определяется, как точная верхняя грань расстояний между точками множества 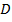. В частности, если 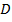– круг, то 
– это как раз длина диаметра круга в обычном смысле. В общем понятие диаметра множества поясняет рисунок:
|
|
|
Ясно, что если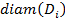 
невелик, то и площадь также невелика, поскольку неравенство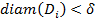 
означает, что содержится некотором в круге радиуса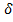 
и имеет площадь не больше, чем 
.
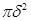Действительно, возьмём произвольную точку множества в качестве центра этого круга. Так как 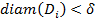, остальные точки лежат внутри круга.
Однако площадь множества может быть невелика, а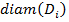 
достаточно велик. Пример – очень тонкий прямоугольник.
Определим диаметр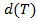 
разбиения T как наибольший из диаметров 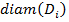частей этого разбиения. Далее, как и в одномерном случае, выберем точки 
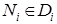(было: 
). Пусть 
имеет координаты 
. Важную роль в дальнейшем будет играть понятие интегральной суммы, определяемой равенством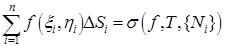 
. Так же, как и в одномерном случае, эта величина имеет простой геометрический смысл. Вспомним, что сумма 
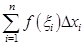представляла собой площадь ступенчатой фигуры вида:
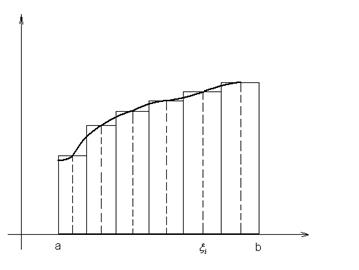
(для простоты считаем, что 
).
Напомним, что объём цилиндра с основанием, имеющим площадь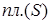 
и с высотой 
равен 
. Поэтому интегральная сумма 
равна объёму тела, состоящего из цилиндров с высотой 
(для простоты считаем, что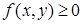 
) и основаниями 
.
Перейдём к основному определению.
Определение. Пусть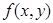 
- ограниченная на квадрируемом множестве 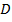функция. Пусть 
. Если
, 
, 
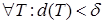
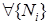, (1)
то будем говорить, что f – интегрируемая на 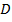функция и что число 
является её интегралом на этом множестве. Используется обозначение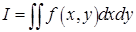 
.
Иногда используют обозначение 
.
Замечание. Это определение несколько отличается от определения обычного определённого интеграла, в котором отсутствовало требование ограниченности функции 
. Дело в том, что для обычного определённого интеграла из выполнения условия (1) следовало необходимое условие интегрируемости: если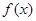 
интегрируема на , то 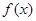ограничена на .
Для двойного интеграла из выполнения условия (1) не следует, что функция 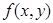ограничена. Это условие, например, заведомо выполняется для любой определённой на множестве 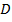функции, если множество 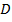имеет равную нулю площадь. Для того, чтобы у двойного интеграла сохранились все важные свойства определённого интеграла и добавлено требование ограниченности функции.
|
|
|
|
|
|
