 |
§5. Связь с вопросом о полном дифференциале
|
|
|
|
§5. Связь с вопросом о полном дифференциале
Если  - дифференцируемая функция двух переменных, то её дифференциал равен
- дифференцируемая функция двух переменных, то её дифференциал равен  .
.
Выясним, при каких условиях на функции 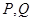 выражение
выражение  представляет собой полный дифференциал, т. е. когда существует такая функция
представляет собой полный дифференциал, т. е. когда существует такая функция  , что
, что  , т. е.
, т. е.  .
.
В предположении непрерывности смешанных производных должно выполняться равенство 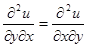 ( теорема Шварца из 2-го семестра), или
( теорема Шварца из 2-го семестра), или  . Докажем, что если
. Докажем, что если 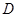 - односвязная область, то верно и обратное.
- односвязная область, то верно и обратное.
Теорема 3. 7. Если в односвязной области 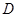 выполняется равенство
выполняется равенство  , то существует дифференцируемая функция
, то существует дифференцируемая функция  такая, что
такая, что  .
.
► Возьмем произвольную точку  и рассмотрим переменную точку
и рассмотрим переменную точку  и любую кривую
и любую кривую  , соединяющую
, соединяющую  с
с  .
.
По следствию теоремы 2,  зависит только от конечной точки
зависит только от конечной точки  и, значит, есть некоторая функция
и, значит, есть некоторая функция  . Покажем, что
. Покажем, что  - искомая функция, т. е.
- искомая функция, т. е.  . Для этого рассмотрим точку
. Для этого рассмотрим точку 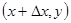 и рассмотрим
и рассмотрим  , где
, где 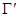 - отрезок прямой, соединяющей точки
- отрезок прямой, соединяющей точки  . На этом отрезке
. На этом отрезке 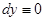 и
и  . Применяя теорему о среднем, получаем (ввиду непрерывности
. Применяя теорему о среднем, получаем (ввиду непрерывности  ), что
), что 
 , где
, где 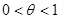 .
.
Тогда
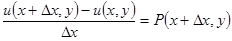 .
.
 .
.
Для  доказательство аналогичное. ◄
доказательство аналогичное. ◄
Замечание. Если векторное поле  обладает свойством
обладает свойством  в односвязной области
в односвязной области 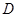 , то говорят, что
, то говорят, что  - потенциальное поле и найденная функция
- потенциальное поле и найденная функция  такая, что
такая, что  , т. е.
, т. е.  , называется потенциалом поля
, называется потенциалом поля  (F=grad u).
(F=grad u).
По определению, если кривая  соединяет
соединяет 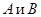 , то работа силового поля
, то работа силового поля  вдоль кривой
вдоль кривой  равна
равна  .
.
Следствие. Если кривая  соединяет точки
соединяет точки 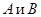 , то работа потенциального поля
, то работа потенциального поля  вдоль
вдоль  равна разности потенциалов
равна разности потенциалов  .
.
► 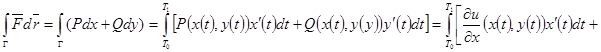

 . ◄
. ◄
В частности, в потенциальном поле работа вдоль любого замкнутого контура  равна 0.
равна 0.
Примечание. Условие односвязности области существенно для справедливости теоремы 3. 5.
Например, если область 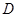 не содержит начала координат, то функции не содержит начала координат, то функции  и и  , а также и их производные , а также и их производные   непрерывны в односвязной области
непрерывны в односвязной области  . Кроме того, выполнено равенство . Кроме того, выполнено равенство  .
По теореме 3. 5 .
По теореме 3. 5 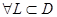 выполнено равенство выполнено равенство  . .
|
С другой стороны, пусть рассматриваемая область 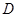 содержит точку
содержит точку  .
.
|
|
|

Рассмотрим  - окружность радиуса - окружность радиуса  , содержащуюся в , содержащуюся в 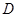 . Рассмотрим параметрические уравнения этой окружности: . Рассмотрим параметрические уравнения этой окружности:
 .
Тогда, по теореме 3. 2 имеем .
Тогда, по теореме 3. 2 имеем
  .
То, что не выполнено заключение теоремы 3. 5 связано с тем, что область, в которой непрерывны .
То, что не выполнено заключение теоремы 3. 5 связано с тем, что область, в которой непрерывны 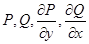 не является односвязной. не является односвязной.
|
Глава 4. Поверхностные интегралы
§1. Площадь поверхности, заданной явным уравнением
Определим сначала площадь поверхности 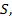 заданной явным уравнением
заданной явным уравнением
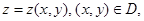 (1)
(1)
где  - плоская область. Примерами таких поверхностей служат изученные Вами в курсе аналитической геометрии плоскости и параболоиды, многие другие поверхности. Предположим, что функция
- плоская область. Примерами таких поверхностей служат изученные Вами в курсе аналитической геометрии плоскости и параболоиды, многие другие поверхности. Предположим, что функция  и её частные производные
и её частные производные  непрерывны в области
непрерывны в области  . Это будет кратко обозначаться так:
. Это будет кратко обозначаться так:  .
.
Пусть  , т. е.
, т. е.  . Уравнение касательной плоскости к поверхности в этой точке имеет вид:
. Уравнение касательной плоскости к поверхности в этой точке имеет вид:  .
.
Далее в этом параграфе мы будем для краткости обозначать  . Напомним, что в общем уравнении плоскости
. Напомним, что в общем уравнении плоскости  числа
числа  представляют собой координаты перпендикулярного к этой плоскости вектора. Значит,
представляют собой координаты перпендикулярного к этой плоскости вектора. Значит, 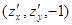 - нормальный вектор к касательной плоскости к поверхности
- нормальный вектор к касательной плоскости к поверхности  в точке
в точке 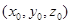 . Будем называть любой вектор, перпендикулярный к касательной плоскости к поверхности
. Будем называть любой вектор, перпендикулярный к касательной плоскости к поверхности  в точке
в точке 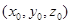 . нормальным вектором к поверхности
. нормальным вектором к поверхности  в точке
в точке 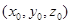 . Вектор
. Вектор 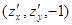 , вообще говоря, не единичный. Чтобы сделать его единичным, его следует умножить на один из нормирующих множителей, т. е. на одно из чисел
, вообще говоря, не единичный. Чтобы сделать его единичным, его следует умножить на один из нормирующих множителей, т. е. на одно из чисел 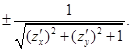 Итак, два единичных вектора нормали к поверхности в рассматриваемой точке имеют вид:
Итак, два единичных вектора нормали к поверхности в рассматриваемой точке имеют вид:

Известно, что координаты единичного вектора – это косинусы углов, составляемых этим вектором с осями  (т. е. с положительными направлениями этих осей), соответственно. Пусть
(т. е. с положительными направлениями этих осей), соответственно. Пусть  . Очевидно, что
. Очевидно, что  . Это означает, что справедливы равенства
. Это означает, что справедливы равенства 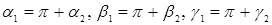 .
.
|
|
|
Предположим, что мы рассматриваем разбиение  этой поверхности на части
этой поверхности на части 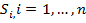 непрерывными кусочно-гладкими кривыми. Под диаметром множества
непрерывными кусочно-гладкими кривыми. Под диаметром множества  понимается точная верхняя грань расстояний между точками этого множества. Диаметр разбиения T – это наибольший из диаметров получившихся частей. Обозначают его
понимается точная верхняя грань расстояний между точками этого множества. Диаметр разбиения T – это наибольший из диаметров получившихся частей. Обозначают его 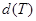 .
.
В каждой полученной части поверхности выберем точку 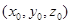 и рассмотрим касательную плоскость к поверхности в этой точке. Пересечения касательных плоскостей ограничат многоугольники, которые образуют «панцирь» на поверхности. Этот «панцирь» состоит из плоских многоугольников и, следовательно, имеет площадь, равную сумме площадей составляющих его многоугольников.
и рассмотрим касательную плоскость к поверхности в этой точке. Пересечения касательных плоскостей ограничат многоугольники, которые образуют «панцирь» на поверхности. Этот «панцирь» состоит из плоских многоугольников и, следовательно, имеет площадь, равную сумме площадей составляющих его многоугольников.
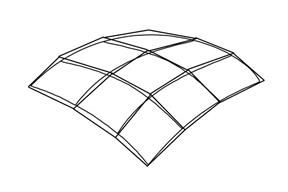
Если при стремлении к 0 диаметра разбиения площади «панцирей» имеют конечный предел, то он и называется площадью поверхности, заданной явным уравнением.
Найдём формулу для вычисления площади такой поверхности. Рассмотрим плоский многоугольник, нормаль к которому имеет направляющие косинусы  . Рассмотрим случай
. Рассмотрим случай  .
.


Без ограничения общности, достаточно рассматривать прямоугольник, причём, для простоты, считаем, что его проекция на плоскость  есть прямоугольник со сторонами
есть прямоугольник со сторонами  , а сам он имеет стороны
, а сам он имеет стороны  .
.
Тогда
 и
и  .
.
В общем случае  .
.
Если нормали выбирались в точках 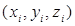 , то пусть
, то пусть 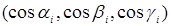 – их направляющие косинусы. Согласно сказанному выше, площадь «панциря» есть
– их направляющие косинусы. Согласно сказанному выше, площадь «панциря» есть 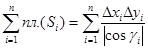 . Эта сумма является интегральной суммой для двойного интеграла
. Эта сумма является интегральной суммой для двойного интеграла 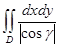 . Как установлено выше,
. Как установлено выше,
 , поэтому
, поэтому 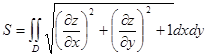 .
.
|
|
|


